Ray Optics and Optical Instruments
Ray Optics and Optical Instruments is a significant chapter in the Class 12 Physics syllabus which deals with the behaviour of light when passing through different media and when interacting with optical surfaces. This chapter teaches students the propagation of light in straight lines, reflection and refraction, as well as image-producing processes with mirrors and lenses. These optical phenomena are explained by physics on the basis of geometrical principles, ray diagrams, and mathematical relations important in the analysis of the formation of images and perception.
This Story also Contains
- Important Topics of Ray Optics and Optical Instruments
- Important Formulas of Ray Optics and Optical Instruments
- Ray Optics and Optical Instruments: Previous Year Questions
- Ray Optics and Optical Instruments in Different Exams
- Important Books and Resources for Class 12: Ray Optics and Optical Instruments
- NCERT Resources for Ray Optics and Optical Instruments
- NCERT Subjectwise Resources
- Practice Questions based on Ray Optics and Optical Instruments
- Conclusion
To learn about ray optics, one must understand the measurement of quantities like angle of incidence, angle of reflection, refractive index, focal length, and magnification, as well as how these are used to study ray optics. It is not enough to say that an image is formed without mentioning its position, size, nature and orientation. Equally, the operation of optical equipment is impossible to describe without introducing laws like Snell's law of refraction as well as other laws like the mirror and lens formula, which connect distances of objects, image distance, and the focal length. Optical behaviour can be analysed and compared using units and well-established relations that work with standard units. Also, this chapter presents the optical instruments, including the human eye, microscope, and telescope and describes how they use lenses and mirrors to improve vision and see objects at a distance or those that are small. It also talks about the common optical defects of the eye and how they can be corrected. The knowledge of these concepts enables students to relate the theoretical material to practical work and offers a solid background to further studies on wave optics, optical technology, and next-generation imaging systems.
Important Topics of Ray Optics and Optical Instruments
Ray Optics and Optical Instruments chapter covers the behaviour of light on the basis of the ray approximation and the way in which mirrors, lenses, and optical instruments form images. The significant topics include reflections, refraction, image forming, optical defects, and instrument working that are very important at both Class 12 board exams and in many competitive exams such as JEE and NEET. A good knowledge of these topics can assist the students in relating geometrical concepts to real-life applications in optics.
1. Reflection of Light
Reflection of Light is the effect whereby rays of light are reflected to go back into the same medium after hitting a reflecting surface. This subject explains the laws of reflection, which explain the relationship between the incident ray, reflected ray and the normal at the point of incidence. It also talks about the way the reflection gives rise to the formation of images, particularly in the flat mirrors. In ray optics, the fundamental optical behaviour and image creation require the understanding of light reflection to analyse it.
2. Spherical Mirrors
Spherical Mirrors are reflecting surfaces that are curved, where the reflecting surface is a part of a sphere. The topic describes the difference between a concave and a convex mirror and the way the mirrors create images through reflection of light. It presents significant concepts such as pole, principal axis, centre of curvature, and focal length, as well as image formation ray diagrams. Knowledge of spherical mirrors is necessary in the study of the properties of images and numerical equations in ray optics.
3. Refraction of Light
The Refraction of Light refers to the effect where the course of light changes upon passing through one transparent medium into another as a result of a change in speed. This topic explains the laws of refraction and introduces the concept of refractive index as a measure of how much a medium slows down light. It assists in the explanation of the behaviour of light in various optical materials. Lenses, prisms and optical instruments are studied based on the principle of refraction.
4. Total Internal Reflection
The phenomenon where light passing out of a denser medium into a rarer medium is entirely reflected back into the former medium at angles of incidence steeper than a particular angle is called Total Internal Reflection. This topic describes the conditions necessary to have complete internal reflection, and it brings out the concept of the critical angle. It also talks about the significant applications of optics, like optical fibres, prisms, and total reflecting apparatus. This concept is very important in associating ray optics with optical technology in real life.
5. Refraction Through a Prism
Refraction through a Prism describes the process in which the light is refracted and redirected as it moves through a triangular glass prism. Some of the crucial terms that are presented in this topic are the angle of deviation and the angle of minimum deviation. It also describes the process of dispersion, in which white light separates into the colours that it consists of. To be able to study spectra and optical characteristics of materials, a deeper insight into refraction with a prism is needed.
6. Spherical Lenses
The Spherical Lenses are transparent optical devices which have a curved surface that is used to refract light to create images. This topic describes the action of convex (converging) and concave lenses and the way these lenses bend the rays of light. It brings about significant notions of optical centre, focal length, principal axis, lens formula and magnification. The study of spherical lenses is fundamental to image formation and the study of optical instruments.
7. Power of a Lens and Combination of Lenses
Power of a Lens and Combination of Lenses is a description of the way in which the strength of a lens to bend light in or out is measured. This topic presents the idea of the power of a lens, its unit dioptre, and the correlation between power and the focal length. It also describes the behaviour of multiple lenses when they are used in combination and the calculation of the combined power of the lenses. This topic is related to the study of optical systems and corrective lenses.
8. Optical Instruments
Optical Instruments are instruments that utilize the lens and mirrors in order to create enlarged or better images of objects. This subject topic describes the fundamental concepts of the formation of an image and the angular magnification in optical devices. It presents the use of lens combinations to improve vision and observation. The knowledge of optical instruments also aids in relating the concepts of ray optics to the applications in science and technology.
9. Human Eye
The human eye is a natural optical tool that is studied as the means of vision, which forms images on the retina. The topic describes the anatomy and functioning of the eye, the purpose of the cornea, lens and retina in the formation of an image. It brings in significant terms like near point, far point and power of accommodation. The study of the human eye can be used to explain vision and optical defects
10. Defects of Vision and Their Correction
Defects of Vision and Their Correction is concerned with the common visual defects, which involve the impairment of the ordinary focusing power of the human eye. The defects described by this topic include myopia, hypermetropia, and presbyopia, and the causes of these defects. It also talks of how these defects can be fixed or remedied using the right convex or concave lenses. This is a useful topic to know in order to interrelate ray optics with visual health in reality.
11. Simple Microscope
A simple microscope is an optical device which is used to magnify small things by using one convex lens. This topic describes such concepts as magnification, image creation and the functioning of a simple microscope. It is also the one that proposes the idea of magnifying power to various viewing conditions. The knowledge of this topic assists in the acquisition of the fundamental concept of optical magnification instruments.
12. Compound Microscope
A compound microscope is an optical device in which two lenses are used, including an objective lens and an eyepiece lens, that are used to produce a grossly magnified view of extremely tiny items. This subject discusses how to construct a compound microscope and how to operate it, as well as how to achieve successive magnification. It brings out the idea of amplifying power when viewed in various conditions. This topic is significant in learning about scientific instruments in laboratories and research.
13. Astronomical Telescope
An astronomical telescope is a telescopic device that is used to see celestial bodies that are too far away, like stars and planets. This topic describes how a telescope should be made and how it should be used with objective and eyepiece lenses. It also defines the idea of angular magnification and explains how the telescope can be adjusted normally. This is a crucial topic to grasp so as to learn how to view distant objects in astronomy in a clear way.
Important Formulas of Ray Optics and Optical Instruments
Significant Formulas of Ray Optics and Optical Instruments give the mathematical relationships needed to study the behaviour of light when it is reflected or refracted, and when mirrors, lenses and optical instruments form images. The equations are used to calculate the position of images, the size, the magnification, as well as the optical power precisely. These formulas need to be practised and used properly in order to solve numerical problems in Class 12 Board Exams and Competitive exams, including JEE Main and NEET.
1. Reflection (Spherical Mirrors):
- Mirror formula
$
\frac{1}{f}=\frac{1}{v}+\frac{1}{u}
$
- Magnification (mirror)
$
m=\frac{h_i}{h_o}=-\frac{v}{u}
$
- Relation between the focal length and the radius of curvature
$
f=\frac{R}{2}
$
2. Refraction (Snell's Law):
- Refractive index
$
\mu=\frac{c}{v}
$
- Snell's law
$
\mu_1 \sin i=\mu_2 \sin r
$
3. Total Internal Reflection:
$\sin C=\frac{1}{\mu}$
4. Refraction Through a Prism
- Angle of deviation
$
\delta=i_1+i_2-A
$
- At minimum deviation
$
\mu=\frac{\sin \left(\frac{A+\delta_m}{2}\right)}{\sin \left(\frac{A}{2}\right)}
$
5. Spherical Lenses:
- Lens formula
$
\frac{1}{f}=\frac{1}{v}+\frac{1}{u}
$
- Magnification (lens)
$
m=\frac{h_i}{h_o}=\frac{v}{u}
$
6. Power of a Lens:
- Power
$
P=\frac{1}{f} \quad \text { (f in metres) }
$
- Combination of lenses in contact
$
P_{\mathrm{eq}}=P_1+P_2+P_3+\ldots
$
7. Simple Microscope:
- Magnifying power (normal adjustment)
$
M=\frac{D}{f}
$
- Magnifying power (final image at near point)
$
M=1+\frac{D}{f}
$
(where $D=25 \mathrm{~cm}$ )
8. Compound Microscope:
- Magnifying power (normal adjustment)
$
M=\frac{L}{f_o} \cdot \frac{D}{f_e}
$
- Magnifying power (final image at near point)
$
M=\frac{L}{f_o}\left(1+\frac{D}{f_e}\right)
$
9. Astronomical Telescope:
- Magnifying power (normal adjustment)
$
M=\frac{f_o}{f_e}
$
- Magnifying power (final image at near point)
$
M=\frac{f_o}{f_e}\left(1+\frac{f_e}{D}\right)
$
Ray Optics and Optical Instruments: Previous Year Questions
Past Year Questions of Ray Optics and Optical Instruments help the students to learn the exam pattern and the most common concepts asked in this chapter. These questions usually involve the topics of reflection and refraction, lenses and mirrors, optical instruments, and numerical problems with references to formulas and ray diagrams. PYQs practice enhances accuracy in problem solving, conceptual clarity, and proves quite helpful in achieving a good score in the Class 12 board examination, JEE Main and NEET.
Question 1:
In a compound microscope, the magnified virtual image is formed at a distance of 25cm from the eyepiece. The focal length of its objective lens is 1cm. If the magnification is 100 and the tube length of the microscope is 20cm, then the focal length of the eyepiece lens (in cm) is:________(Give answer up to 2 decimal points)
Solution:
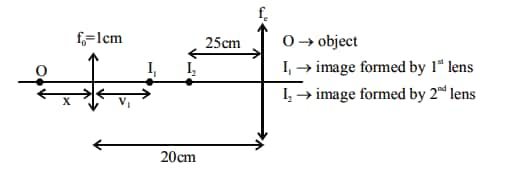
As the Lens formula is given as
$
\frac{1}{v}-\frac{1}{u}=\frac{1}{f}
$
For the first lens
$
\Rightarrow \frac{1}{\mathrm{v}_1}-\frac{1}{-\mathrm{x}}=\frac{1}{1} \Rightarrow \mathrm{v}_1=\frac{\mathrm{x}}{\mathrm{x}-1}
$
also magnification $\left|\mathrm{m}_1\right|=\left|\frac{\mathrm{v}_1}{\mathrm{u}_1}\right|=\frac{1}{\mathrm{x}-1}$
for $2^{\text {nd }}$ lens this is acting as object
$
\text { so } u_2=-\left(20-v_1\right)=-\left(20-\frac{x}{x-1}\right)
$
and $v_2=-25 \mathrm{~cm}$
$
\text { angular magnification }=\left|\mathrm{m}_2\right|=\left|\frac{\mathrm{D}}{\mathrm{u}_2}\right|=\frac{25}{\left|\mathrm{u}_2\right|}
$
Total magnification $\mathrm{m}=\mathrm{m}_1 \mathrm{~m}_2=100$
$
\begin{aligned}
& \Rightarrow\left(\frac{1}{x-1}\right)\left(\frac{25}{20-\frac{x}{x-1}}\right)=100 \\
& \frac{25}{20(x-1)-x}=100 \Rightarrow 1=80(x-1)-4 x \\
& \Rightarrow 76 x=81 \Rightarrow x=\frac{81}{76}
\end{aligned}
$
$
\Rightarrow \mathrm{u}_2=-\left(20-\frac{81 / 76}{81 / 76-1}\right)=\frac{-19}{5}
$
Now apply the lens formula for the eyepiece
$
\frac{1}{-25}-\frac{1}{-19 / 5}=\frac{1}{f_e} \Rightarrow f_e=\frac{25 \times 19}{106} \approx 4.48 \mathrm{~cm}
$
Question 2:
A biconcave lens is made of glass with a refractive index of 1.5 and has radii of curvature of 20 cm and 30 cm. If the 20 cm surface is silvered, then the effective focal length of the mirror formed is:
Solution:
For silvered lens - $\frac{1}{f_e}=\frac{1}{f_m}-\frac{2}{f_l}$
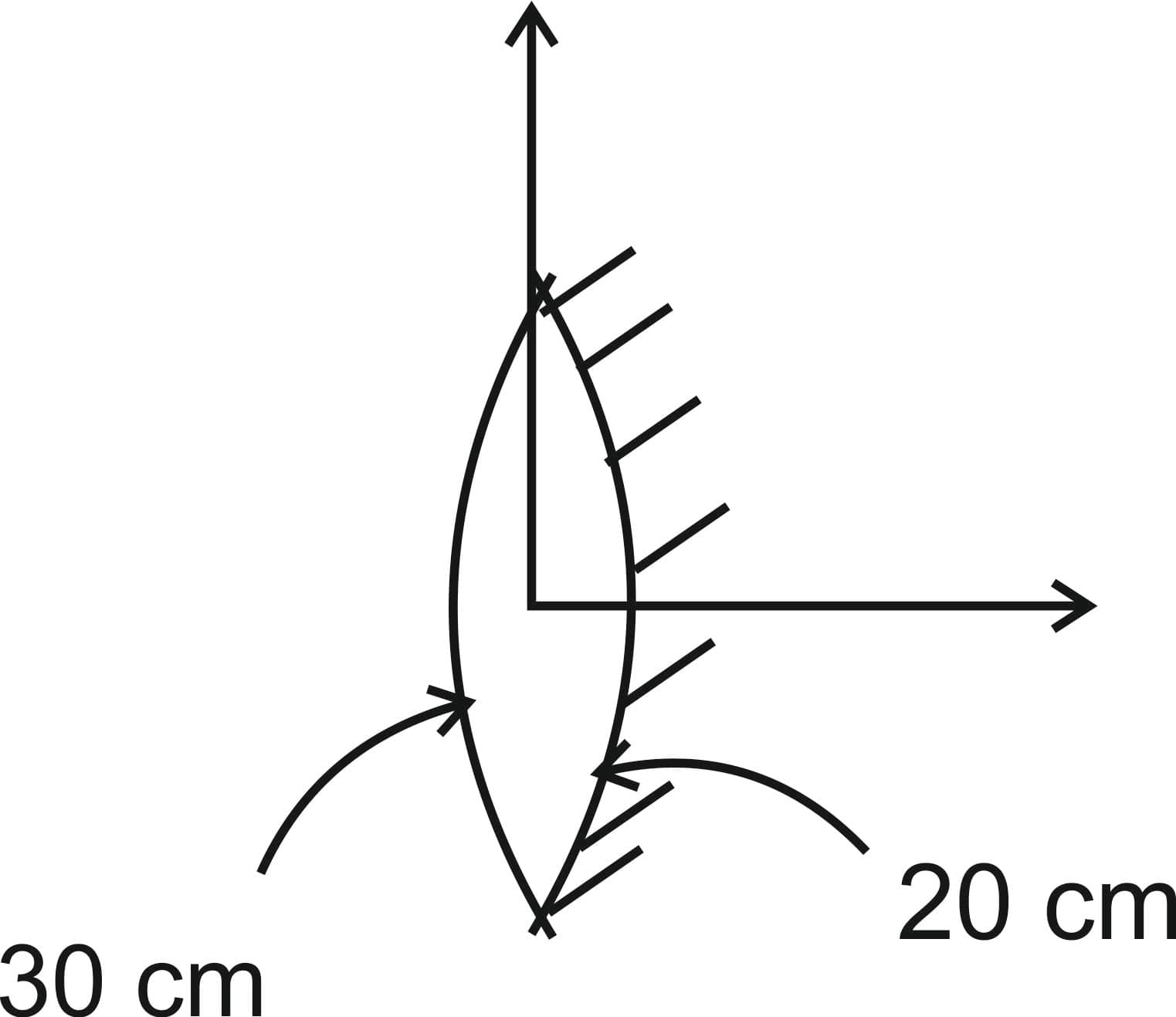
Therefore, focal length of lens $\frac{1}{f_e}=(1.5-1)\left(\frac{1}{30}-\frac{1}{-20}\right)$ or $f_e=24 \mathrm{~cm}$
Focal length of the mirror, $f_m=\frac{R_2}{2}=\frac{-20}{2}=-10 \mathrm{~cm}$
Effective focal length of silverd lens is, $\frac{1}{f_e}=\frac{1}{f_m}-\frac{2}{f_e} \Rightarrow f_e=\frac{-60}{11} \mathrm{~cm}$
The silvered convex lens behaves as a concave mirror of focal length $\frac{60}{11} \mathrm{~cm}$.
Question 3:
A diverging lens with a magnitude of focal length 25 cm is placed at a distance of 15 cm from a converging lens with a magnitude of focal length 20 cm. A beam of parallel light falls on the diverging lens. The final image formed is :
Solution:
Given the focal length of the concave lens f = - 25 cm
Focal length of convex lens f' = 20 cm
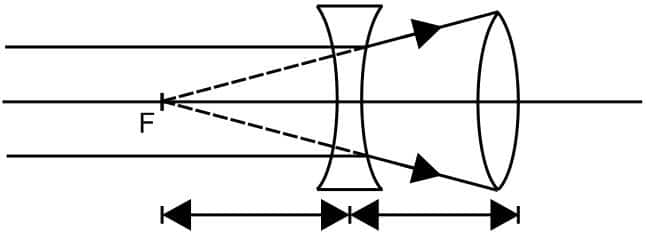
The image of a diverging lens will form at F. i.e. at the focal length of the concave lens.
Now this image will serve as the object for the convex lens, it is at twice the focal length of the convex lens (i.e., - 2f), which is at a distance of 40 cm from the convergent lens.
Ray Optics and Optical Instruments in Different Exams
Ray Optics and Optical Instruments is a high-weightage chapter in Class 12 Physics, which involves not only conceptual learning but also numerical solution of problems. This chapter has questions that cover knowledge of reflection, refraction, the formation of images, and the working of optical instruments, and thus is important in board exams and competitive exams. The knowledge of the exam-wise focus assists the students in preparing better and scoring higher.
| Exam | Focus Areas | Common Questions Asked | Marks / Questions Weightage | Preparation Tips |
|---|---|---|---|---|
| JEE Main | Mirrors, lenses, prisms, optical instruments | Numerical problems on lens/mirror formula, prism deviation | 2–3 questions (8–12 marks) | Practice numericals, master the sign convention |
| JEE Advanced | Ray diagrams, optical instruments, prism | Conceptual + multi-step numerical questions | 1–2 questions (8–16 marks) | Focus on derivations, ray diagrams, and concepts |
| NEET | Mirrors, lenses, defects of vision, microscopes | Direct formula-based and conceptual MCQs | 2–3 questions (8–12 marks) | Revise the NCERT theory and formulas thoroughly |
| UPSC CDS / NDA | Basic ray optics, defects of vision | Conceptual and simple numericals | 1–2 questions (2–4 marks) | Focus on definitions and basic formulas |
| State-Level Exams (WBJEE, MHT CET, etc.) | Lenses, mirrors, prisms, eye defects | Conceptual + numerical MCQs | 2–3 questions (8–12 marks) | Practice previous year questions |
| GATE | Optical instruments, refraction principles | Conceptual and numerical questions (rare) | Rare / 1 question (2–5 marks) | Focus on clarity of fundamentals |
| School-Level (CBSE, ICSE, State Boards) | Entire chapter | Short answers, numericals, and ray diagrams | 8–12 marks | Practice ray diagrams and NCERT examples |
| CUET | Conceptual understanding | MCQs, assertion-reason questions | 2–3 questions (6–9 marks) | Revise concepts and basic numericals |
| SSC & Banking Exams | Basic optics facts | One-liners, matching | 1 question (1–2 marks) | Focus on definitions and applications |
Important Books and Resources for Class 12: Ray Optics and Optical Instruments
In order to perform well in Ray Optics and Optical Instruments chapter in Class 12 Physics, the student is advised to use high-quality textbooks, reference guides, and problem solving tactics which clearly explain the theory and problem solving tactics. Such resources include vital areas like reflection, refraction, lenses, mirrors, prisms, optical instruments and eyewear correction, so they are useful when preparing for board examinations as well as competitive examinations like JEE Main, JEE Advanced and NEET.
| Book Title | Author / Publisher | Description |
|---|---|---|
| NCERT Class 12 Physics (Part II) | NCERT | The official textbook covering all ray optics and optical instruments topics with clear explanations, diagrams, and NCERT exercises. |
| NCERT Exemplar Physics (Class 12) | NCERT | Contains higher-order thinking, application-based, and challenging questions related to mirrors, lenses, prisms, and optical instruments. |
| Concepts of Physics – Volume 2 | H.C. Verma | Excellent for building deep conceptual understanding and solving challenging optics problems with detailed explanations and examples. |
| Understanding Physics: Optics & Modern Physics | D.C. Pandey (Arihant) | Comprehensive topic-wise coverage with solved examples and practice questions focused on ray optics and optical instruments. |
| Physics for Class 12 | R.D. Sharma | Provides step-by-step theory along with a wide variety of solved and unsolved numerical problems on optics and instrument design. |
| Arihant All-In-One Physics (Class 12) | Arihant | Offers concise theory summaries, solved examples, and practice questions, including previous year questions on ray optics. |
| MTG Chapter-wise Previous Year Questions – Physics | MTG | Helps students practice and analyse past questions specifically from the Ray Optics and Optical Instruments chapter across exams. |
NCERT Resources for Ray Optics and Optical Instruments
The best source of learning to understand the behaviour of light when it passes through mirrors, lenses, prisms, and optical devices is the NCERT material of Ray Optics and Optical Instruments, which is very reliable and covers the syllabus. The NCERT textbook and exemplar problems explain key concepts such as reflection, refraction, image formation, and the working of optical instruments in a structured manner. Such materials are necessary to give a strong base and succeed in Class 12 board exams and other competitive exams such as JEE Main and NEET.
NCERT Subjectwise Resources
NCERT subject-wise materials are organised and syllabus-based learning content on various subjects, which assists students in developing a good conceptual basis. They consist of textbooks, exemplar problems, and solutions and can thus be very helpful in the preparation for the board exams and even competitive exams such as JEE and NEET.
Practice Questions based on Ray Optics and Optical Instruments
Practice Questions on Ray Optics and Optical Instruments help students strengthen their understanding of how light behaves during reflection and refraction and how images are formed by mirrors, lenses, and optical devices. These questions revolve around ray diagrams, numeric problems involving mirror and lens formulas, concepts as far as prisms are concerned and how optical equipment works. Regular practice improves accuracy, conceptual clarity, and confidence in problem-solving. Answering a broad range of questions is very useful not only in Class 12 board examinations but also in competitive examinations such as JEE Main and NEET.
Conclusion
In the chapter Ray Optics and Optical Instruments, a solid conceptual background to the study of the behaviour of light and the way images are formed by means of reflections and refraction is established. Through frequent revision of basic concepts, significant formulas, ray diagrams, and principles of mirrors, lenses, and prisms, and optical instruments, the students will gain a clear and precise understanding of concepts. Such structured planning increases confidence, and it is very effective to give good performance in Class 12 board exams and in competitive exams such as JEE Main and NEET.
Frequently Asked Questions (FAQs)
Concave mirrors curve inward and can create both real and virtual images, while convex mirrors curve outward and only produce virtual images.
A converging lens is thicker in the middle and can form both real and virtual images, while a diverging lens is thinner in the middle and only produces virtual images.
The focal length of a lens is the distance between the lens and its focal point, where parallel rays of light converge or appear to converge after passing through the lens.
Total internal reflection occurs when light travelling from a denser medium to a less dense medium strikes the boundary at an angle greater than the critical angle. This causes the light to be completely reflected back into the denser medium instead of being refracted