Real Depth And Apparent Depth

The concepts of real depth and apparent depth offer fascinating insights into how we perceive the world around us. Real depth refers to the actual distance between objects in a medium, while apparent depth is the perceived distance due to the refraction of light as it passes through different substances. This phenomenon is not just a theoretical concept but has practical implications in everyday life. For example, when you look at a pool of water, the bottom seems closer than it actually is due to the refraction of light. Similarly, the apparent depth of an object submerged in water can be misleading, which is crucial in fields like underwater photography, fishing, and even medical imaging.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Real Depth and Apparent Depth
2. Solved Example Based on Real Depth and Apparent Depth
3. Hence, the answer is the option (4).
4. Summary

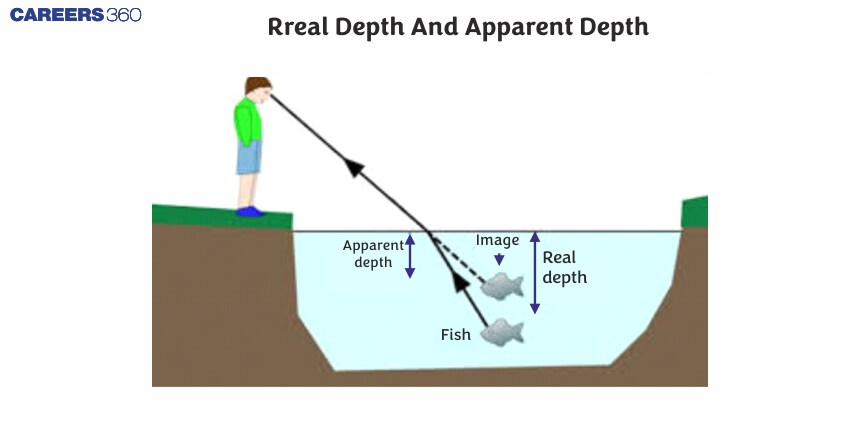
Understanding these optical principles helps us navigate and interpret visual information more accurately in various contexts, from designing more effective optical instruments to simply enjoying a day at the beach. Let's discuss the concept of Real depth and Apparent depth and some solved examples for better understanding.

Real Depth and Apparent Depth

The concepts of real depth and apparent depth describe how we perceive the distance of objects in different media. Real depth is the actual distance between an object and the surface of a medium, such as the true depth of a lake or the distance of an object below the surface of water. On the other hand, apparent depth is the perceived distance of the object, which often differs from the real depth due to the refraction of light as it passes from one medium to another, such as from air into water. Here are two cases

Case 1:

When an object is in a denser medium and the observer is in the rarer medium.

If the object and observer are situated in different mediums then due to refraction, the object appears to be displaced from its real position.

Here O is the real position of the object and O is the apparent position of the object as seen by the observer. 'h' is the real depth of the object from the surface of the water and h' is the apparent depth of the object. is the density of the medium where the object is placed. is the density of the rarer medium.

$\frac{\mu_2}{\mu_1}=\frac{\text { Real depth }}{\text { Apparent depth }}=\frac{h}{h^{\prime}}$..

Therefore, Real depth > Apparent depth.

Apparent Shift

The term "apparent shift" refers to the change in the perceived position of an object due to the refraction of light as it passes through different media. This shift occurs because light bends when it moves from one medium to another with different densities, such as from air into water or from air into glass.

$d=h-h^{\prime}=\left(1-\frac{\mu_1}{\mu_2}\right) h$

Case 2:

The object is in a rarer medium and the observer is in the denser medium.

$\frac{\mu_2}{\mu_1}=\frac{\text { Apparent depth }}{\text { Real depth }}=\frac{h^{\prime}}{h}$..

Therefore, apparent depth > real depth.

Apparent shift

$l=\left(\frac{\mu_1}{\mu_2}-1\right) h$

The image of point p when viewed from the top of the slabs will be

(both the top slab and bottom slab have refractive index=$\mu=1.5$)

Recommended Topic Video

Solved Example Based on Real Depth and Apparent Depth

Example 1: An observer can see through a pinhole the top end of a thin rod of height h, placed as shown in the figure. The beaker's height is 3h and its radius is h. When the beaker is filled with a liquid up to a height of 2h, he can see the lower end of the rod. Then the refractive index of the liquid is

1) $5 / 2$
2) $\sqrt{\frac{5}{2}}$
3) $\sqrt{\frac{3}{2}}$
4) $\frac{3}{2}$

Solution:

The line of sight of the observer remains constant, making an angle of 45° with the normal.

$\begin{aligned} & \sin \theta=\frac{h}{\sqrt{h^2+(2 h)^2}}=\frac{1}{\sqrt{5}} \\ & \mu=\frac{\sin 45^{\circ}}{\sin \theta}=\frac{1 / \sqrt{2}}{1 / \sqrt{5}}=\sqrt{\left(\frac{5}{2}\right)}\end{aligned}$

Hence, the answer is the option (2).

Example 2: There is a small source of light at some depth below the surface of water (refractive index $=\frac{4}{3}$ ) in a tank of large cross-sectional surface area. Neglecting any reflection from the bottom and absorption by water, the percentage of light that emerges out of the surface is (nearly) :

[ Use the fact that the surface area of a spherical cap of height h and radius of curvature r is $2 \pi r h$ ]

1) $34 \%$
2) $17\%$
3) $50%$
4) $21%$

Solution:

$
\sin \beta=\frac{3}{4}, \cos \beta=\frac{\sqrt{7}}{4}
$

Solid angle $d \Omega=2 \pi R^2(1-\cos \beta)$
Percentage of light $=$
$
\frac{2 \pi R^2(1-\cos \beta)}{4 \pi R^2} \times 100=\frac{1-\cos \beta}{2} \times 100=\left(\frac{4-\sqrt{7}}{8}\right) \times 100 \approx 17^{\circ} \%
$

Hence, the answer is the option (2).

Example 3: The image of point p when viewed from the top of the slabs will be (both the top slab and bottom slab have refractive index=$\mu=1.5$)

1) 2 cm above p

2) 1.5 cm above p

3) 2 cm below p

4) 1 cm above p

Solution:

Apparent Shift (Δd)

$\Delta d=d\left(1-\frac{n_r}{n_i}\right)$

wherein

$n_i=$ Refractive index of the medium of the incident.
$n_r=$ Refractive index of the medium of refraction.
$\mathrm{d}=$ distance of object.

$\begin{aligned} & d=2\left(1-\frac{1}{\mu}\right) t=2\left(1-\frac{1}{1.5}\right)(1.5) \mathrm{cm} \\ & =1.0 \mathrm{~cm}\end{aligned}$

Therefore final image will be 1 cm above point p.

Hence, the answer is the option (4).

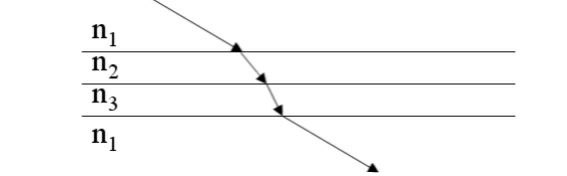
Example 4: A tank contains three layers of immiscible liquid. The first layer is of water with (r.i. $\frac{4}{3}$ ) and a thickness 8 cm. The second layer is of oil with r.i. $\frac{3}{2}$ and thickness of 9 cm, while the third layer is of glycerine with r.i. 2 and thickness 4 cm. The apparent depth of the bottom is :

1) 10cm

2) 12cm

3) 14cm

4) 16cm

Solution:

Refraction across multiple slabs

$
\text { Apparent depth }=\frac{t_1}{\mu_1}+\frac{t_2}{\mu_2}+-----+\frac{t_n}{\mu_n}
$

wherein

$t_1, t_2----t_n$ are the thickness of the medium
$\mu_1, \mu_2----\mu_n$ are Refractive index of the medium
Apparent depth
$
\begin{aligned}
& =\frac{d_1}{\mu_1}+\frac{d_2}{\mu_2}+\frac{d_3}{\mu_3} \\
& =\left(\frac{8}{\frac{4}{3}}+\frac{p}{\frac{3}{2}}+\frac{4}{2}\right) \mathrm{cm} \\
& \text { depth } \\
& =14 \mathrm{~cm}
\end{aligned}
$

Hence, the answer is the option (3).

Example 5: A microscope is focused on an object at the bottom of a bucket. If liquid with a refractive index $\frac{5}{3}$ is poured inside the bucket, then the microscope has to be raised by 30 cm to focus the object again. The height of the liquid in the bucket is :

1) 12 cm
2) 50 cm
3) 18 cm
4) 75 cm

Solution:

$\begin{aligned} & \mathrm{d}_{\text {app }}=\frac{\mathrm{d}}{\mu}=\frac{\mathrm{h}}{(5 / 3)} \\ & \text { Shift }=\mathrm{h}-\frac{3 \mathrm{~h}}{5}=30 \\ & \mathrm{~h}=75 \mathrm{~cm}\end{aligned}$

Hence, the answer is the option (4).

Summary

Real depth and apparent depth are crucial concepts in optics, describing how we perceive distances in different media due to light refraction. Real depth is the actual distance of an object from the surface, while apparent depth is the perceived distance, which can be altered by the medium's refractive index. Apparent shift occurs when an object's position appears displaced due to light bending between different media. Practical examples include determining the refractive index of a liquid, calculating the percentage of light emerging from a water surface, and measuring depth changes in multi-layered liquids. Understanding these principles is essential for accurate visual interpretation and optical device calibration