Relation Between G and g
The relation between g (acceleration due to gravity) and G (universal gravitational constant) forms a fundamental concept in gravitational physics. G is a constant that defines the strength of the gravitational force between two masses in the universe, while g represents the acceleration experienced by an object due to Earth's gravitational pull. The relation between the two can be expressed mathematically using Newton's law of gravitation, which helps in understanding how the mass and radius of a celestial body, like Earth, influence the gravitational acceleration experienced at its surface.
Let's read this article to learn about the difference between capital g and small g, and the value of G on different surfaces. This is one of the very important concept for Class 12 Board exams and competitive exams like JEE, NEET and other state engineering exams.
This Story also Contains
- Acceleration due to gravity (g) on earth
- Universal Gravitational Constant (G)
- Relation Between Acceleration Due to Gravity (g) and Gravitational Constant (G)
- Variation in the Value of Acceleration Due to Gravity (g)
Also read -
Acceleration due to gravity (g) on earth
An object which falls under the sole influence of our gravity is called a free-falling object or acceleration due to gravity.
A free-falling object usually has an acceleration of about 9.8 m s−2, downward towards the earth. We usually denote it with the symbol g.
-
Acceleration due to gravity g on earth formula:
$g=9.8 \mathrm{~m} / \mathrm{s}^2$ -
Acceleration due to gravity dimensional formula = $M^0 L^1 T^{-2}$
Universal Gravitational Constant (G)
Universal Gravitational Constant (G)
The Universal Gravitational Constant, denoted by $G$, is a fundamental constant in physics that appears in Newton's Law of Gravitation. It measures the strength of the gravitational force between two objects.
Newton's Law of Gravitation:
$
F=G \frac{m_1 m_2}{r^2}
$
Where:
- $F=$ gravitational force between two masses
- $m_1, m_2=$ masses of the two objects
- $r=$ distance between the centers of the masses
- $G=$ Universal Gravitational Constant
- SI Unit of G:
Newton meter $^2$ per kilogram ${ }^2$ - The dimensional formula for G: $[G]=M^{-1} L^3 T^{-2}$
Relation Between Acceleration Due to Gravity (g) and Gravitational Constant (G)
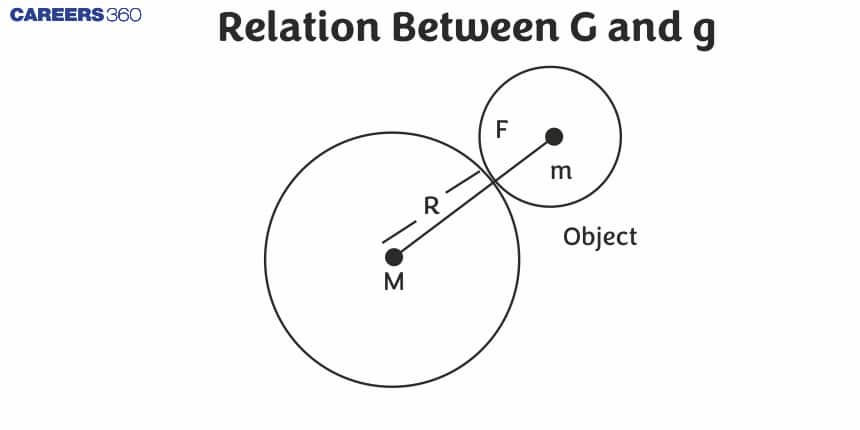
The acceleration due to gravity $g$ on the surface of a planet depends on the mass of the planet and its radius, as well as the Universal Gravitational Constant (G).
From Newton's Law of Gravitation, the force on an object of mass $m$ on the surface of the Earth is:
$
F=G \frac{M m}{R^2}
$
Where:
$M=$ mass of the Earth, $R=$ radius of the Earth
But $F=m g$, so equating:
$
m g=G \frac{M m}{R^2}
$
Dividing both sides by $m$ :
$
g=G \frac{M}{R^2}
$
The acceleration due to gravity $g$ is directly proportional to the mass of the planet and inversely proportional to the square of its radius, with $G$ as the proportionality constant.
Variation in the Value of Acceleration Due to Gravity (g)
In the above section we have seen the relation between g and G, Now let's move to a little depth of how the g value is changing in different cases.
It may vary due to the following factors
(i) Height above the surface of the earth
(ii) Depth below the surface of the earth
(iii) Shape of the earth
Let's read one by one starting from height above the surface of the earth.
(i) Height above the surface of the earth
Suppose a body of mass m is lying on the surface of the earth and its radius is R. Then its acceleration due to gravity at the earth's surface,
$g=\frac{G M}{R^2}$
Height h above the surface, the force of gravity,
$F=\frac{G M m}{(R+h)^2}$
Therefore, the acceleration due to gravity at height h above the surface
$g^{\prime}=\frac{G M}{(R+h)^2}$
Or,
$\begin{gathered}g^{\prime}=\frac{G M}{R^2} \cdot \frac{1}{\left(1+\frac{h}{R}\right)^2} \\ g^{\prime}=g \cdot \frac{1}{\left(1+\frac{h}{R}\right)^2}\end{gathered}$
Thus,
$g^{\prime}<g$
(ii) Depth below the surface of the earth
Now for this situation, let's suppose an object of mass m is kept at a depth of d below the earth's surface. Its distance from the center of the Earth is (R − d). This mass is located on the outer surface of the Inner solid sphere. The gravitational pull on a mass within a spherical shell is always zero. Consequently, the Objects experience gravitational attraction mainly because the Inner solid sphere
Mass of this sphere
$M^{\prime}=M \cdot \frac{(R-d)^3}{R^3}$
Here, M represents the mass of the entire sphere of radius R.
Now, the force of gravity on an object at a depth d
$
F=\frac{G M^{\prime} m}{(R-d)^2}
$
Substitute $M^{\prime}=M \cdot \frac{(R-d)^3}{R^3}$ into the equation:
$
F=\frac{G \cdot\left(M \cdot \frac{(R-d)^3}{R^3}\right) m}{(R-d)^2}
$
Simplify:
$
F=\frac{G M m(R-d)}{R^3}
$
Since,
$g=\frac{G M}{R^2}$-----(1)
After substituting the value in equation (1),
$g^{\prime}=g \cdot\left(1-\frac{d}{R}\right)$
(iii) Shape of the earth
The earth is not a perfect sphere. It is somewhat flat at the two poles. The equatorial radius (R eq ) is approximately 21 km more than the polar radius ( R p ).
$g_p=\frac{G M}{R_p^2}$
Acceleration due to gravity at the equator,
$g_{e q}=\frac{G M}{R_{e q}^2}$
∵$R_p$<$R_eq$
∴$g_p$>$g_{eq}$
by going through this article which starts with the difference between capital g and small g, and covers the relation between G and g along with the last value of g in different surfaces you have a solid understanding of this concept. Solve numerical types of questions based on this concept to boost your confidence before the final board exam or any competitive exams.
Related Topics,
Also, check-
Frequently Asked Questions (FAQs)
The cosmic law of gravity (cited by Isaac Newton) formed the basis for the description of the planets orbiting the sun and the orbits of satellites orbiting the planets.
Gravity is made up of quantum particles. These quantum particles are called gravitons. These gravitons are lightweight, but they contain energy.
g = GM / R2
The acceleration of gravity is usually denoted by a small g and the universal gravitational constant is often denoted by a capital G.