Relative Velocity - Definition, Formula, FAQs

Looking outside the window of a moving train means seeing that another stationary train appears to be moving backward. How does a stationary train appear to move? Behind it lies a crucial concept of Relative Motion, which will help us explain why objects move differently in different frames. Suppose you are driving a car and you overtake the other car from behind. What happens is that the driver from the car behind you sees the car coming in the backward direction and eventually goes back. However, the person standing on the ground doesn’t see it as the car moving backward, although the driver behind sees it that way.

This Story also Contains

1. What Is Relative Velocity?
2. Formula to Calculate Relative Velocity
3. Cases of Relative Velocity
4. Examples of Relative Velocity
5. Solved Example Based on Relative Velocity

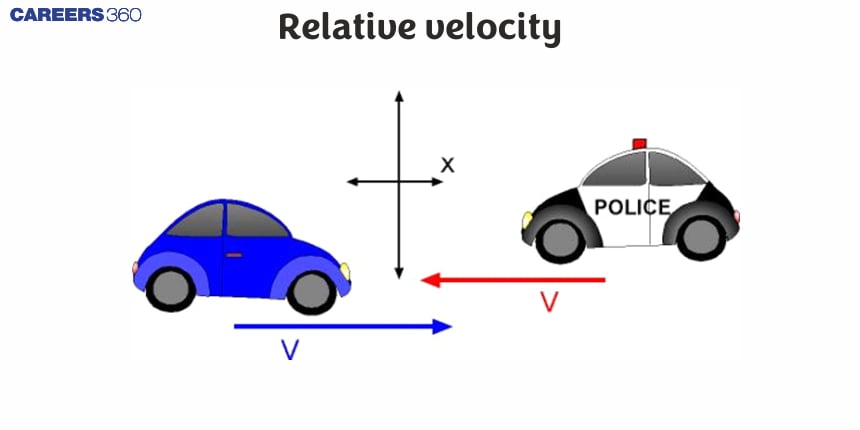
In this article, we will cover the concept of relative velocity This concept falls under the broader category of kinematics which is a crucial chapter in Class 11 Physics.

What Is Relative Velocity?

The rate of change in the position of one object concerning another object with time is defined as the Relative Velocity of one object with another.

Mathematically, relative velocity can be represented as:

Relative velocity of object A concerning object B.

$ \vec{V}_{A B}=\vec{V}_A-\vec{V}_B$

Also read -

• NCERT Exemplar Solutions for All Subjects
• NCERT Notes For All Subjects
• NCERT Solutions for All Subjects

Formula to Calculate Relative Velocity

1. When Two Objects Move in the Same Direction:

$$
V_{\text {relative }}=V_{\mathbf{1}}-V_2
$$
Where:

• $V_1$ is the velocity of the first object.
• $V_2$ is the velocity of the second object.

2. When Two Objects Move in Opposite Directions:

$$
V_{\text {relative }}=V_{\mathbf{1}}+V_2
$$
Where:

• $V_1$ is the velocity of the first object.
• $V_2$ is the velocity of the second object.

3. For Two-Dimensional Motion (Vector Form):

If the velocities of two objects are given as vectors $\vec{V}_1$ and $\vec{V}_2$, the relative velocity is calculated as:

$$
\vec{V}_{\text {relative }}=\vec{V}_1-\vec{V}_2
$$

Here, subtraction is done using vector operations, accounting for both magnitude and direction.

Cases of Relative Velocity

Let's start with some important case

• When A and B are moving along a straight line in the same direction.

$ \begin{aligned}
& \overrightarrow{V_A}=\text { Velocity of object } A . \\
& \overrightarrow{V_B}=\text { Velocity of object } B \text {. }
\end{aligned}$

Then, the relative velocity of A w.r.t B is:

$
\vec{V}_{A B}=\vec{V}_A-\vec{V}_B
$
$\vec{V}_{A B}, \vec{V}_A, \vec{V}_B$ all are in the same direction. (If $\vec{V}_A>\vec{V}_{B \text { ) }}$

And Relative velocity of B w.r.t A is

$\begin{aligned}
\vec{V}_{B A} & =\vec{V}_B-\vec{V}_A \\
\& \vec{V}_{A B} & =-\vec{V}_{B A}
\end{aligned}$

• When A & B are moving along with straight line in the opposite direction.

The relative velocity of A concerning B is.

$\begin{aligned}
& \vec{V}_{A B}=\vec{V}_A-\vec{V}_B \\
& V_{A B}=V_A+V_B
\end{aligned}$

• Relative Velocity when bodies moving at an angle $\theta$ to each other

Relative velocity of a body, A with respected body B

$
\begin{aligned}
V_{A B} & =\sqrt{V_A^2+V_B^2+2 V_A V_B \cos (180-\theta)} \\
& =\sqrt{V_A^2+V_B^2-2 V_A V_B \cos (\theta)}
\end{aligned}
$

Where,
$V_A=$ velocity of $A$
$V_B=$ velocity of $B$
$\theta=$ angle between $A$ and $B$

• $\text { If } \overrightarrow{V_{A B}} \text { makes an angle } \beta \text { with the direction of } \overrightarrow{V_A} \text {, then }$

$ \begin{aligned}
& \tan \beta=\frac{V_B \sin (180-\theta)}{V_A+V_B \cos (180-\theta)} \\
& =\frac{V_B \cdot \sin \theta}{V_A-V_B \cos \theta}
\end{aligned}$

• If two bodies are moving at right angles to each other

Relative Velocity of A concerning B is:

$V_{A B}=\sqrt{V_A^2+V_B^2}$

Examples of Relative Velocity

• Cars Overtaking: A faster car overtakes a slower car on the way. Where their velocity is the relative velocity, that is the speed difference.
• Boat in a River: A boat floats on it as well as sails on the surface of the water during a river’s current. The boat and the riverbank speed is the sum, of the speed of the boat and the speed of the running water stream.
• Walking on an Escalator: As you might have observed, if you try to walk on a moving escalator, your speed with regard to the ground enhances or diminishes the speed of the moving escalator depending on the direction you are moving.
• Trains Passing Each Other: In cases where two trains are going in opposite directions, then their relative velocity is the sum of each train's velocity.

Recommended Topic Video

Solved Example Based on Relative Velocity

Example 1: A train is moving at 50 km/h and a man is running at 20 km/h in a direction opposite to the direction of the train. The relative velocity of the train (in km/h ) concerning man is

1) 70

2)30

3)60

4)40

Solution:

When A & B are moving along with straight line in the opposite direction.

$
\begin{aligned}
& \vec{V}_A=\text { Velocity of object } \mathrm{A} . \\
& \vec{V}_B=\text { Velocity of object } \mathrm{B} \text {. }
\end{aligned}
$

The relative velocity of $A$ concerning $B$ is.
$
\vec{V}_{A B}=\vec{V}_A-\left(-\vec{V}_B\right)
$
$-\vec{V}_B$ is because of the opposite direction.
$
\vec{V}_{A B}=\vec{V}_A+\left(\vec{V}_B\right)
$

As per question
$
\overrightarrow{V_R}=V_T+V_M
$

= ( 50 + 20 ) km/h

= 70 km/h

Hence, the answer is option (1).

$V_{A B}=\sqrt{V_A^2+V_B^2+2 V_A V_B \cos (180-\theta)}$

Example 2: Person A is moving along east and B is moving along north. The relative velocity of A concerning B is :$(\left.V_A=10 \mathrm{~m} / \mathrm{s}, V_B=10 \sqrt{3} \mathrm{~m} / \mathrm{s}\right)$

1) 20 m/s along north

2) 20 m/s along south

3) 20 m/s along 120⁰ with east

4) None of the above

Solution:

$\begin{aligned}
& \overrightarrow{V_A}=\text { Velocity of object } A \text {. } \\
& \overrightarrow{V_B}=\text { Velocity of object } B .
\end{aligned}$

$\text { The relative velocity of } \mathrm{B} \text { wrt to } \mathrm{A} \text { is } V_{BA}$

$\begin{aligned}
& \overrightarrow{V_{B / A}}=\overrightarrow{V_B} \cdot \overrightarrow{V_A}=10 \sqrt{3} \hat{j}-10 \hat{\imath} \\
& \left|\overrightarrow{V_{B / A}}\right|=\sqrt{100+300}=20 \mathrm{~m} / \mathrm{s} \\
& \tan \theta=\frac{V_B}{V_A}=\frac{10 \sqrt{3}}{10}=\sqrt{3} \\
& \text { So } \theta=60^{\circ} \text { from west } \\
& \text { i.e } \theta=120^{\circ} \text { from east }
\end{aligned}$

Hence, the answer is option (3).

Related Topics:

• Distance and Displacement
• Speed And Velocity
• Boat River Problem
• Vector Addition And Vector Subtraction

Example 3: Rain is falling vertically downward with a speed of 4 km/h. A girl moves on a straight road with a velocity of 3km/h. The apparent speed (in m/s) of rain with respect to the girl is:

1) 5

2) 4

3) 3

4) 7

Solution :

$
\overrightarrow{V_{R / G}}=\overrightarrow{V_R}-\overrightarrow{V_G}
$
$\mathrm{V}_{\mathrm{R}}=$ Velocity of rain wrt ground, $\mathrm{V}_{\mathrm{G}}=$ Velocity of girl wrt ground
$
\left|\overrightarrow{V_{R / G}}\right|=\sqrt{V_R^2+V_G^2}=\sqrt{3^2+4^2}=5 \mathrm{~km} / \mathrm{h}
$

Hence, the answer is option (1).

Example 4: A particle A is moving along north with a speed of 3 m/s and another particle B is moving with a velocity of 4 m/s at 60^o with north, then the velocity of B as seen by A is

1) $5 \mathrm{~m} / \mathrm{s}$
2) $3.5 \mathrm{~m} / \mathrm{s}$
3) $\sqrt{13} \mathrm{~m} / \mathrm{s}$
4) $\sqrt{15} \mathrm{~m} / \mathrm{s}$

Solution:

The relative velocity of a body, A with respected body B when the two bodies moving at an angle $\theta$ is:

$\begin{aligned}
& V_{A B}=\sqrt{V_A^2+V_B^2+2 V_A V_B \cos (180-\theta)} \\
& =\sqrt{V_A^2+V_B^2-2 V_A V_B \cos (\theta)} \\
& \left|\vec{V}_{A B}\right|=\sqrt{V_A^2+V_B^2-2 V_A V_B \cdot \cos \theta} \\
& =\sqrt{3^2+4^2-2 \times 3 \times 4 \times \frac{1}{2}}=\sqrt{13} \mathrm{~m} / \mathrm{s} \\
&
\end{aligned}$

Hence, the answer is option (3).

Example 5: A particle A is moving along the x-axis and a particle B is moving along the y-axis. The speed of A is 6m/s and that of B is 8 m/s, then the velocity (in m/s) of A concerning B is:

1) 10

2) 12

3) 8

4) 14

Solution:

Relative Velocity of $\mathrm{A}$ with respect to $\mathrm{B}$ is
$
\begin{aligned}
& V_{A B}=\sqrt{V_A^2+V_B^2} \\
& V_{A B}=\sqrt{V_A^2+V_B^2}=\sqrt{8^2+6^2}=10 \mathrm{~m} / \mathrm{s}
\end{aligned}
$

Hence, the answer is option (1).