Resonance Column Method

The Resonance Column Method is a fascinating experimental technique used in physics to determine the speed of sound in air. This method involves creating standing waves in a column of air, typically within a cylindrical tube, by adjusting the length of the air column and observing the points where resonance occurs. In real life, the principles of resonance can be seen in musical instruments like flutes or organ pipes, where the length of the air column determines the pitch of the sound produced. Just as a musician adjusts the length of a flute to create different notes, the Resonance Column Method allows us to explore the relationship between the physical properties of a medium and the speed of sound through it. By understanding this concept, we can appreciate how sound travels through different environments, from the strings of a guitar to the echo in a canyon.

This Story also Contains

1. Resonance Column Method
2. Solved Examples Based on Resonance Column Method
3. Summary

Resonance Column Method

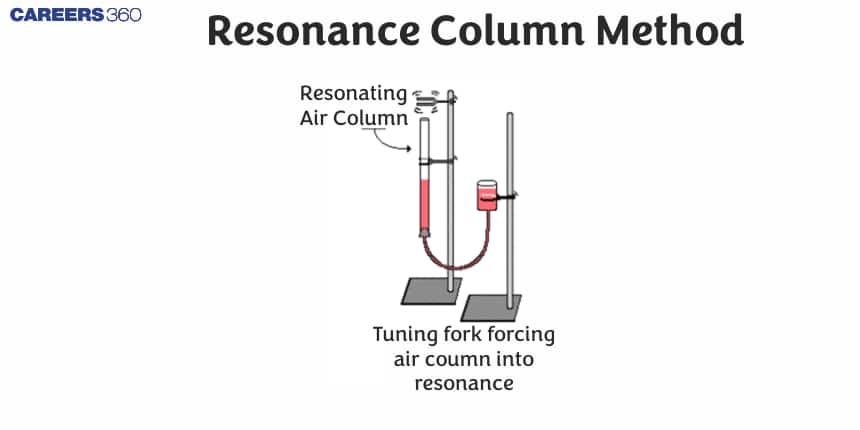
The Resonance Column Method is an important experimental technique in physics used to determine the speed of sound in air. This method involves using a vertical cylindrical tube partially filled with water, where sound waves are introduced at the open end. By adjusting the length of the air column above the water level, resonance occurs at specific points, allowing the measurement of the wavelength and, subsequently, the speed of sound.

In this, the equipment used is a resonance tube. This apparatus is used to determine the velocity of sound in air and to compare the frequency of two turning forks.

It is a closed organ pipe with a variable length of air column. When we brought a turning fork near it, its air column vibrated with the frequency of the fork. The length of the air column varied until the frequency of the fork and the air column became equal. When frequency becomes equal, the column resonates and the note becomes loud.

It is the full setup of the resonance tube. If a tuning fork of known frequency $n_o$ is struck on a rubber pad and brought near the open end. Because of this, the air column starts oscillating. This air column behaves as a closed organ pipe and the water level is a closed end. We decrease the water level gradually and as the water level reaches a position where there is a node of the corresponding stationary wave, in the air column, resonance takes place. At this place intensity of sound will be maximum.

Let at this position the length of the air column is $l_1$. By further decreasing water level again after some distance maximum intensity of sound is obtained where the node is obtained. Let this level be $l_2$.

If the length of the first and second resonance, then

$\begin{array}{rl}& l_1+e=\frac{\lambda }{4}\text{and}{l}_2+e=\frac{3\lambda }{4}\\ & \text{so,}\lambda =2(l_2-l_1)\end{array}$

Speed of sound in air at room temperature $v=n\lambda =2n(l_2-l_1)$

Also,

$\begin{array}{c}\frac{l_2+e}{l_1+e}=3\\ \Rightarrow l_2=3l_1+2e\end{array}$

So, the second resonance is obtained at a length more than thrice the length of the first resonance.

Recommended Topic Video

Solved Examples Based on Resonance Column Method

Example 1: In a resonance tube experiment when the tube is filled with water up to a height of 17.0 cm from the bottom, it resonates with a given tuning fork. When the water level is raised the next resonance with the same tuning fork occurs at a height of 24.5 cm. If the velocity of sound in air is $330\mathrm{m}/\mathrm{s}$, the tuning fork frequency is :

1) 2200 Hz
2) 550 Hz
3) 1100 Hz
4) 3300 Hz

Solution:

$\begin{array}{rl}& \mathrm{L}-{\mathrm{h}}_1=\mathrm{n}\frac{\lambda }{2}+\frac{\lambda }{4}\\ & \mathrm{L}-{\mathrm{h}}_2=(\mathrm{n}-1)\frac{\lambda }{2}+\frac{\lambda }{4}\\ & \Rightarrow \frac{\lambda }{2}={\mathrm{h}}_2-{\mathrm{h}}_1=24.5-17.0=7.5\mathrm{cm}\\ & \Rightarrow \lambda =15\mathrm{cm}\\ & \mathrm{u}=\mathrm{f}\lambda \\ & \mathrm{f}=2200\mathrm{Hz}\end{array}$

Hence, the answer is the option (1).

Example 2: The first overtone frequency of an open organ pipe is equal to the fundamental frequency of a closed organ pipe. If the length of the closed organ pipe is 20 cm. The length of the open organ pipe is __________cm.

1)80

2)60

3)70

4)100

Solution:

For open organ pipes,
${\mathrm{f}}_{\mathrm{n}}=\frac{\mathrm{nv}}{2\mathrm{l}}\to (1)$

For closed organ pipe
${\mathrm{f}}_{\mathrm{n}}=\frac{(2\mathrm{n}-1)\mathrm{v}}{4\mathrm{l}}\to (2)$

For the first overtone of an open organ pipe
$\begin{array}{rl}& \mathrm{n}=2\left(2^{\text{nd}}\text{mode}\right)\\ & {\mathrm{f}}_1=\frac{2\mathrm{v}}{2{\mathrm{l}}_1}\to \text{(3)}\end{array}$

Fundamental frequency of closed organ pipe, $n=1$
$\begin{array}{rl}& {\mathrm{f}}_2=\frac{\mathrm{v}}{4{\mathrm{l}}_2}\to (4)\\ & {\mathrm{f}}_1={\mathrm{f}}_2\text{(Given)}\\ & \frac{2\mathrm{v}}{2{\mathrm{l}}_1}=\frac{\mathrm{v}}{4{\mathrm{l}}_2}\\ & {\mathrm{l}}_1=4{\mathrm{l}}_2\\ & =4(20)\\ & =80\mathrm{cm}\end{array}$

The length of the open organ pipe is 80 cm.

Hence, the answer is the option (1).

Example 3: In an experiment to determine the velocity of sound in air at room temperature using a resonance tube, the first resonance is observed when the air column has a length of 20.0 cm for a tuning fork of frequency 400 Hz. The velocity of the sound at room temperature is $336{\mathrm{ms}}^{-1}$. The third resonance is observed when the air column has a length of ________cm

1) 104

2) 300

3) 750

4) 3456

Solution:

$\begin{array}{rl}& 400=\frac{\mathrm{V}}{4({\mathrm{L}}_1+\mathrm{e})}-(\mathrm{i})\\ & 400=\frac{5\mathrm{V}}{4({\mathrm{L}}_2+\mathrm{e})}-(\mathrm{ii})\\ & {\mathrm{L}}_1+\mathrm{e}=\frac{\lambda }{4}=21\mathrm{cm}\\ & {\mathrm{L}}_2+\mathrm{e}=\frac{5\lambda }{4}=105\mathrm{cm}\\ & \mathrm{e}=1\mathrm{cm},{\mathrm{L}}_2=104\mathrm{cm}\end{array}$

Hence, the answer is the option (1).

Example 4: A tuning fork is vibrating at 250 Hz The length of the shortest closed organ pipe that will resonate with the tuning fork will be _______cm. (Take the speed of sound in air as $340{\mathrm{ms}}^{-1}$)

1) 34cm

2) 35cm

3) 36cm

4) 33cm

Solution:

$f=250\mathrm{Hz}$

For the shortest closed organ pipe

$\begin{array}{rl}& l=\frac{\lambda }{4}\\ & \lambda =4l\end{array}$

At resonance,
$\begin{array}{rl}& f_{\text{organ pipe}}=f_{\text{tuning fork}}\\ & \frac{V}{\lambda }=250\\ & \frac{340}{4(l)}=250\\ & l=340\times {10}^{-3}\\ & l=0.34\mathrm{m}\\ & l=34\mathrm{cm}\end{array}$

Hence, the answer is the option (1).

Example 5: In Quicks tube was employed and a tuning fork of frequency 1328 Hz was used. Initially, it was on max intensity. Later when the slider tube was drawn by a distance of 12.5 cm, the intensity was found maximum for the first time. Find the speed of sound in the air

1) 332 m/s

2) 330 m/s

3) 336 m/s

4) 328 m/s

Solution:

Quinck's tube

This is an apparatus used to demonstrate the phenomena of interference and also to measure the velocity of sound in air.

wherein

$\begin{array}{rl}& x=\frac{\lambda }{2}\\ & V=2{\nu }_{0}x\\ & {\nu }_0=\text{frequency}\\ & \text{double path means}=25\mathrm{cm}\\ & \lambda =25\mathrm{cm}\\ & v=1328\times 25\mathrm{cm}=332\mathrm{m}/\mathrm{s}\end{array}$

Hence, the answer is the option (1).

Summary

The Resonance Column Method is a fundamental experimental technique in physics used to measure the speed of sound in air. By creating standing waves in a variable-length air column, this method demonstrates the principles of resonance, much like how musical instruments produce sound. It utilizes a cylindrical tube partially filled with water and a tuning fork to create resonance at specific air column lengths. The technique not only helps in determining the speed of sound but also in comparing the frequencies of different tuning forks. Through various examples, the method’s application is illustrated, emphasizing its role in understanding wave phenomena.