Scalars and Vectors - Definition, Examples, Types, FAQs

Q: Difference between scalar and vector quantity.

Scalar quantity: A scalar property is one that can only be described in terms of magnitude. Scalar can be used to describe a variety of quantities in physics. Distance, mass, temperature, speed, and energy are only a few examples. Vector quantity: Vector is a quantity that can be described in both the terms of magnitude and direction. A vector is a directed line segment in geometry. Certain quantities in physics can only be described using vectors. Force, velocity, displacement, position vector, acceleration, linear momentum, and rotational momentum are all examples.

Q: Define vector product.

The vector product is a vector with a magnitude equal to the product of the magnitudes of two vectors plus the sine of the angle between them, also known as the cross product of two vectors.

Q: How do you represent a vector quantity graphically?

A vector quantity is typically represented graphically as an arrow. The length of the arrow indicates the magnitude of the vector, and the direction the arrow points shows the vector's direction.

Q: Can a vector quantity ever be zero even if its components are non-zero?

Yes, a vector quantity can be zero even if its components are non-zero. This occurs when the components cancel each other out. For example, if you walk 3 meters north and then 3 meters south, your displacement (a vector quantity) is zero, even though you moved in both directions.

Q: What is the significance of unit vectors in vector representation?

Unit vectors are vectors with a magnitude of 1 and are used to indicate direction. They are significant because they allow us to express any vector as a combination of its components along standard directions (usually x, y, and z axes in 3D space).

Q: How does scalar multiplication affect a vector?

Scalar multiplication changes the magnitude of a vector but not its direction. Multiplying a vector by a positive scalar increases its magnitude, while multiplying by a negative scalar reverses its direction and may change its magnitude.

Q: What is the difference between vector addition and scalar addition?

Vector addition takes into account both magnitude and direction, often using methods like the parallelogram rule or tip-to-tail method. Scalar addition simply involves adding the numerical values of quantities with the same units.

Scalars and Vectors - Definition, Examples, Types, FAQs

Edited By Vishal kumar | Updated on Jul 02, 2025 04:35 PM IST

Vectors are fundamental elements in physics and mathematics, representing quantities that have both magnitude and direction. Unlike scalar quantities, which can be simply added or subtracted using basic arithmetic, vector operations require special consideration of their directional components. Understanding vector addition and subtraction is essential for accurately describing physical phenomena such as forces, velocities, and displacements.

This Story also Contains

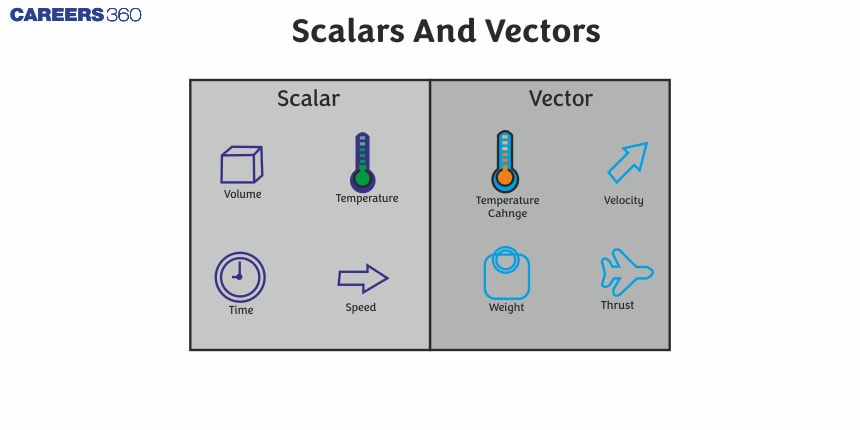
Physical Quantity:
What is Scalar quantity and give scalar quantity examples:
What is vector quantity and give vector quantity examples:
Different types of vector:
Solved Example Based on Scalar and Vector
Summary

Scalars and Vectors - Definition, Examples, Types, FAQs

This article delves into the methods for identifying vectors and scalers starting with the definition of scalers, vectors and different types of vectors and their properties, which belongs to the chapter kinematics, which is an important chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), one question has been asked on this concept directly and many indirectly in NEET as well.

Physical Quantity:

A physical quantity is a matter or system property that can be measured and quantified. At least two attributes are held by all physical quantities. The first is the numerical magnitude, and the second is the unit of measurement.

Types of physical quantities:

There are seven basic physical quantities.

Length, Mass, Time, Temperature, Current, luminous intensity, and amount of substances.

Some quantities in physics have simply magnitude, some have both magnitude and direction. It is fundamental to know the properties of vectors and scalars in order to understand these physical quantities.

What is Scalar quantity and give scalar quantity examples:

Scalar definition and Scalar meaning: A scalar property is one that can only be described in terms of magnitude. Scalars can be used to describe a variety of quantities in physics. Distance, mass, temperature, speed, and energy are only a few examples. A scalar value is a single value; a scalar number can never be negative because it just has magnitude and no direction.

For instance, consider the terms string number, variable, and column. In contrast to a set of values, a scalar value is a single value. Every point in space is represented mathematically as a scalar value.

A scalar is a field element that is used to define a vector space. Physical scalar fields can be thought of as a subset of more general fields like vector fields, spinor fields, and tensor fields, while scalars are usually thought of as special cases of multi-dimensional quantities like vectors and tensors.

Relativistic scalar: The variations between the outcomes of (four-component, two-component, or one-component “scalar”) relativistic quantum theoretical computations using a finite and infinite speed of light are known as relativistic effects. Electric charge, proper time and proper length space time intervals, and invariant mass are all scalar quantities in relativity.

The Higgs field is the only fundamental scalar quantum field that has been detected in nature. Scalar quantum fields, on the other hand, appear in many effective field theory models of physical processes.

Also read -

What is vector quantity and give vector quantity examples:

Vector definition and Vector quantity meaning: Vector is a quantity that can be described in both the terms of magnitude and direction. A vector is a directed line segment in geometry. Certain quantities in physics can only be described using vectors.

Force, velocity, displacement, position vector, acceleration, linear momentum, and rotational momentum are all examples.

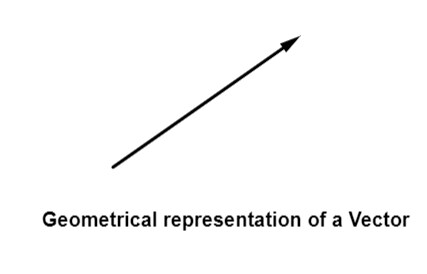
Geometrical representation of a vector

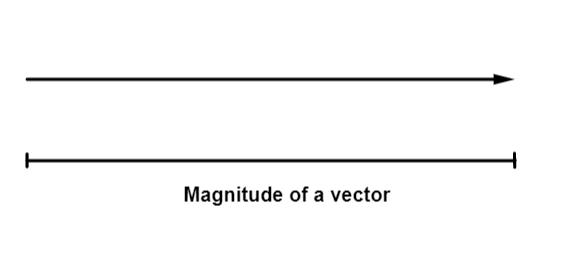
Magnitude of a vector:

The length of a vector determines its magnitude. The magnitude of a vector is sometimes referred to as the vector's norm. For a vector A, the magnitude or norm is denoted by A.

Magnitude of a vector

Related Topics Link,

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Different types of vector:

Equal vectors

a) Collinear vectors

i) Parallel vectors

ii) Anti-parallel vectors

Unit vector
Orthogonal unit vectors

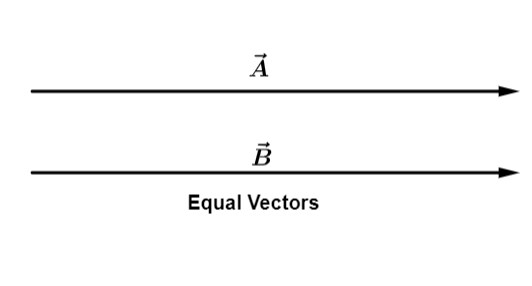
Equal vectors:

Two vectors A and B are said to be equal since it have equal magnitude as well as same direction along with represent the same physical quantity.

Equal vector

a) Collinear vectors:

Vectors that behave in the same direction are known as collinear vectors. The angle between them can be 0oor 180o

i) Parallel vectors:

The angle formed by two vectors A and B acting in same direction along same line is 0o.

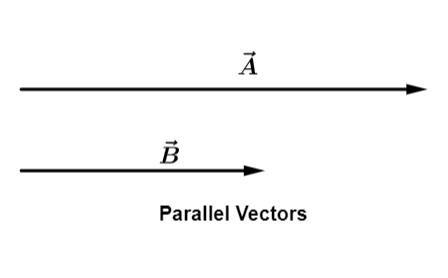
Parallel vectors

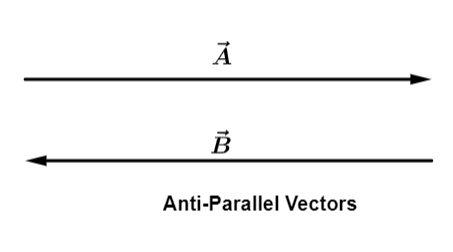
ii) Anti-parallel vectors:

When two vectors A and B are in opposite directions along same line, they are said to be antiparallel. The angle between them is then 180o.

Anti-parallel vectors

Unit vector:

A unit vector is a vector whose magnitude is divided by its length. The unit vector for A is denoted by A. It has a magnitude of one or unity. As a result, we can declare that the unit vector just provides the vector quantity's direction.

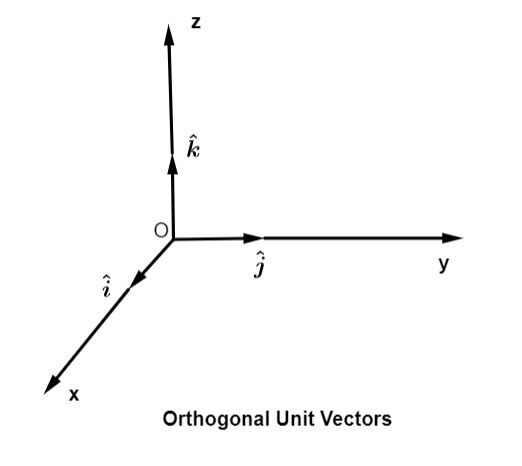
Orthogonal unit vectors:

i, j and k are examples of orthogonal vectors. Orthogonal vectors are two vectors that are perpendicular to each other.

Orthogonal unit vectors

Addition of vectors:

The approach of standard algebra cannot be used to add vectors since they have both magnitude and direction. As a result, vectors can be added geometrically or analytically using vector algebra methods. The triangular law of addition or parallelogram law of vectors approach is used to discover the sum or resultant of two vectors that are inclined to each other.

By triangular law of addition method,

Magnitude of resultant vector,

$R = \sqrt{A^{2} + B^{2} + 2 A B \cos θ}$

The direction of the resultant vector is given by:

$\tan α = \frac{B \sin θ}{A + B \cos θ}$

Subtraction of vectors:

Because vectors have both magnitude and direction, the approach of regular algebra cannot be used to subtract two vectors. As a result, this subtraction can be done analytically or geometrically.

The magnitude of the resultant vector,

$| A - B | = \sqrt{A^{2} + B^{2} - 2 A B \cos θ}$

The direction of the resultant vector is given by:

$\tan α = \frac{B \sin θ}{A - B \cos θ}$

Multiplication of vector by a scalar:

A vector A multiplied by a scalar results in another vector A. If is a positive number, then A is also in the direction of A. It is a negative number, then A is in the opposite direction to the vector A

Scalar product of two vectors:

Definition:

The scalar product, often known as the dot product of two vectors, is made up of vectors and the angle's cosine.

Thus, if there are two vectors A and B having an angle of between them, then their scalar product is defined as A . B=AB cosθ. Here, A and B are magnitudes of A and B.

Properties of scalar product:

Note: Here A, B and C are vectors.

The product quantity A . B is always a scalar. It is positive, when the angle between the vectors is acute i.e. <90o and it is negative if the angle between them is obtuse i.e. 90^o<<180^o
The scalar product is commutative i.e. A . B=B . A
The vectors obey distributive law i.e. A . (B+C)=A . B+A.C
The angle between the vectors =A.B/|AB|
The scalar product of two vectors will be maximum when cosθ=1 i.e. =0^o, when the vectors are parallel, (A . B)_max=AB
The scalar product of two vectors will be minimum, when cosθ=-1 i.e. =180^o, when the vectors are antiparallel, (A . B)_mi_n=-AB
The scalar product of a vector with itself is termed a self-dot product.
If two vectors A and B are perpendicular to each other, then their scalar product is A.B=0, because cos90^o=0. Then the vectors are said to be mutually orthogonal.

Also Read:

Vector product of two vectors:

Definition:

The vector product is a vector with a magnitude equal to the product of the magnitudes of two vectors plus the sine of the angle between them, also known as the cross product of two vectors. The product vector is perpendicular to the plane containing the two vectors, according to the right-hand screw rule or right-hand thumb rule.

Properties of vector product:

Note: Here A, B and C are vectors.

It is not commutative to take the vector product of two vectors. A × B=-[B ×A]
The magnitude of the vector product of two vectors will be the greatest, when sinθ=1 that is =90^o, When the vectors A and B are perpendicular to one another.

(A × B)_max=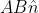 $AB\hat{n}$

The vector product of the two non-zero vectors will be minimum when sinθ=0 i.e. =0oor 180^o

(A × B)_min=0

i.e. If the vectors are parallel or antiparallel, the vector product of two non-zero vectors vanishes.

The null vector is the self-cross product, which is the product of a vector with itself. In physics, the null vector is simply referred to as zero.

Vector products are used to define a variety of quantities in physics. The vector products are used to construct physical quantities that represent rotational effects, such as torque and angular momentum.

Position vector:

A position vector is a scalar that represents the position of a particle in relation to some reference frame or coordinate system at any given time.

Solved Example Based on Scalar and Vector

Example: Which among the following is a scalar quantity?

1) Angular velocity

2) Displacement

3) (correct) Current

4) Area of a planar surface

Solution:

Scalars: Physical quantities can be described completely by their magnitude only but no particular direction. Physical quantities which are scalars Distance, speed, work, etc.

Angular velocity, displacement, and area of the planar surface is a vector quantity because it has a specific direction. Current is a scalar quantity.

Hence, the answer is the option (3).

Example 2: Which of the following is false about scalar quantity?

1) A scalar quantity has magnitude only

2) A scalar can be either positive or negative

3) A scalar quantity can never be negative

4) None of the above

Solution:

As we learned,

Scalars are positive, negative or zero (E.g., temperature, T = -2 Degree C).
Represented by alphabet only A, B, C.
These physical quantities follow normal algebraic rules of addition.

Hence, the answer is the option (3).

Example 3: Which of the following sets has all the vector quantity only?

1) Current, power, Force and velocity

2) Force, torque, moment of inertia, velocity

3) Acceleration, velocity, torque, momentum

4) Speed, displacement, velocity, Force

Solution:

Vectors -Physical quantities can be described by their magnitude and directions.

E.g. Displacement, force, velocity, etc. are vectors. And current, power, moment of inertia, and speed are scalar quantities.

Hence, the answer is the option (3).

Q 4. Which of the following is not a type of vector?

1) Equal vector

2) Collinear vector

3) Co-initial vector

4) Special Vector

Solution:

Types of vectors

There are four types of vectors.

1- Equal vectors

2- Negative vectors

3- Collinear vectors

4- Co-initial vectors

Hence, the answer is the option (4).

Q 5. Two vectors are said to be equal if

1) The magnitude of the two vectors is the same.

2) The direction of two vectors is the same

3) Both magnitude and direction are the same

4) none of the above

Solution:

Equal vectors: Two vectors are said to be equal if they have equal magnitude and the same directions.

Hence, the answer is the option (3).

Summary

In physics, scalar and vector are the physical quantities in the natural world. Scalars are physical quantities that simply have a size or a numerical value (magnitude). You can determine the quantity of something using a scalar.

Also check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. Difference between scalar and vector quantity.

Scalar quantity:

A scalar property is one that can only be described in terms of magnitude.
Scalar can be used to describe a variety of quantities in physics.
Distance, mass, temperature, speed, and energy are only a few examples.

Vector quantity:

Vector is a quantity that can be described in both the terms of magnitude and direction.
A vector is a directed line segment in geometry. Certain quantities in physics can only be described using vectors.
Force, velocity, displacement, position vector, acceleration, linear momentum, and rotational momentum are all examples.

2. What are the different types of vector?

Different types of vector:

Equal vectors

a) Collinear vectors

i) Parallel vectors

ii) Anti-parallel vectors

Unit vector
Orthogonal unit vectors

3. Define unit vector.

4. Define scalar or dot product.

The scalar product, often known as the dot product of two vectors, is made up of vectors and the angle's cosine.

5. Define vector product.

The vector product is a vector with a magnitude equal to the product of the magnitudes of two vectors plus the sine of the angle between them, also known as the cross product of two vectors.

6. How do you represent a vector quantity graphically?

A vector quantity is typically represented graphically as an arrow. The length of the arrow indicates the magnitude of the vector, and the direction the arrow points shows the vector's direction.

7. Can a vector quantity ever be zero even if its components are non-zero?

Yes, a vector quantity can be zero even if its components are non-zero. This occurs when the components cancel each other out. For example, if you walk 3 meters north and then 3 meters south, your displacement (a vector quantity) is zero, even though you moved in both directions.

8. What is the significance of unit vectors in vector representation?

Unit vectors are vectors with a magnitude of 1 and are used to indicate direction. They are significant because they allow us to express any vector as a combination of its components along standard directions (usually x, y, and z axes in 3D space).

9. How does scalar multiplication affect a vector?

Scalar multiplication changes the magnitude of a vector but not its direction. Multiplying a vector by a positive scalar increases its magnitude, while multiplying by a negative scalar reverses its direction and may change its magnitude.

10. What is the difference between vector addition and scalar addition?

Vector addition takes into account both magnitude and direction, often using methods like the parallelogram rule or tip-to-tail method. Scalar addition simply involves adding the numerical values of quantities with the same units.

11. How do scalars and vectors behave differently under coordinate transformations?

Scalars remain unchanged under coordinate transformations because they only have magnitude. Vectors, however, may change their component values under coordinate transformations while maintaining their overall magnitude and direction in space.

12. What is the physical meaning of vector multiplication?

Vector multiplication can have different physical meanings depending on the type of multiplication. The dot product often represents work done or power, while the cross product can represent torque or angular momentum. These operations help describe complex physical interactions.

13. Can you add or subtract scalars and vectors?

No, you cannot directly add or subtract scalars and vectors because they are fundamentally different types of quantities. Scalars can only be added to or subtracted from other scalars, while vectors can only be added to or subtracted from other vectors.

14. What is the difference between a free vector and a bound vector?

A free vector can be moved anywhere in space without changing its meaning, as long as its magnitude and direction are preserved. A bound vector, also called a position vector, has a specific starting point that is significant to its meaning, typically the origin of the coordinate system.

15. How does the concept of vectors apply to circular motion?

In circular motion, vectors are crucial for describing quantities like velocity and acceleration. The velocity vector is always tangent to the circle, while the acceleration vector points towards the center of the circle (centripetal acceleration). The changing direction of these vectors explains the circular path.

16. Can you add two scalar quantities with different units?

No, you cannot add scalar quantities with different units. Scalar addition is only possible for quantities with the same units. For example, you can add two distances, but you cannot add distance and time directly.

17. What is the physical significance of a negative scalar quantity?

A negative scalar quantity often indicates a direction opposite to what is considered positive in the context of the problem. For example, negative acceleration might mean deceleration, or negative temperature in Celsius indicates below freezing.

18. Can a quantity be both scalar and vector depending on the context?

No, a quantity is inherently either scalar or vector. However, related quantities might be scalar or vector. For example, speed (scalar) and velocity (vector) are related but distinct quantities describing motion.

19. What is the difference between distance and displacement?

Distance is a scalar quantity that measures the total length of the path traveled by an object. Displacement is a vector quantity that measures the straight-line distance and direction from the starting point to the ending point, regardless of the path taken.

20. How does the addition of a scalar to a vector differ from scalar multiplication of a vector?

Adding a scalar to a vector is not a valid operation, as they are different types of quantities. Scalar multiplication of a vector, however, is valid and results in a new vector with changed magnitude and possibly reversed direction, but maintaining the same line of action.

21. What is the fundamental difference between a scalar and a vector quantity?

A scalar quantity has only magnitude, while a vector quantity has both magnitude and direction. For example, speed is a scalar quantity, while velocity is a vector quantity.

22. What is the difference between speed and velocity?

Speed is a scalar quantity that measures how fast an object is moving, regardless of direction. Velocity is a vector quantity that measures both how fast an object is moving and in what direction it is traveling.

23. What is the importance of vectors in describing motion?

Vectors are crucial in describing motion because they allow us to represent both the magnitude and direction of physical quantities like velocity, acceleration, and force. This complete description is essential for accurately predicting and analyzing the motion of objects.

24. Can two vectors with different magnitudes and directions ever be equal?

No, two vectors are considered equal only if they have the same magnitude and direction. Vectors with different magnitudes or directions are not equal, even if they might produce the same effect in some specific scenarios.

25. How does the dot product of two vectors differ from their cross product?

The dot product of two vectors results in a scalar quantity, representing how much the vectors are aligned with each other. The cross product, on the other hand, results in a vector perpendicular to both original vectors, representing the area of the parallelogram formed by them.

26. How do you determine if two vectors are perpendicular?

Two vectors are perpendicular if their dot product equals zero. This means that the cosine of the angle between them is zero, which occurs when the angle is 90 degrees.

27. How do you find the angle between two vectors?

The angle between two vectors can be found using the dot product formula. If a and b are two vectors, the angle θ between them is given by: cos(θ) = (a · b) / (|a| |b|), where |a| and |b| are the magnitudes of the vectors.

28. Can you subtract vectors? If so, how?

Yes, you can subtract vectors. Vector subtraction is equivalent to adding the negative of a vector. Graphically, this means reversing the direction of the vector being subtracted and then adding it to the other vector using the tip-to-tail method.

29. What is a null vector?

A null vector, also known as a zero vector, is a vector with zero magnitude. It has no specific direction and is often represented as a point. The null vector is the result of adding a vector to its opposite.

30. How do you find the magnitude of a vector?

The magnitude of a vector is calculated using the Pythagorean theorem. For a 2D vector with components (x, y), the magnitude is √(x² + y²). For a 3D vector (x, y, z), it's √(x² + y² + z²).

31. What is meant by the term 'vector resolution'?

Vector resolution is the process of breaking down a vector into its components along different axes. Typically, a vector is resolved into perpendicular components, such as horizontal and vertical components in a 2D plane.

32. What is a position vector?

A position vector is a vector that represents the position of a point in space relative to a chosen origin. It extends from the origin to the point in question, providing both the distance and direction from the origin to that point.

33. What is the physical significance of the direction of a vector?

The direction of a vector indicates the orientation in which the quantity acts or points. For example, the direction of a velocity vector shows which way an object is moving, while the direction of a force vector indicates which way the force is pushing or pulling.

34. Can you have negative vectors?

The term "negative vector" is not typically used. However, a vector can point in the opposite direction to what is considered positive. This is often represented by a negative sign in front of the vector or its components.

35. What is the importance of frame of reference when dealing with vectors?

The frame of reference is crucial when dealing with vectors because vector quantities like velocity and displacement are measured relative to a specific point or system. Changing the frame of reference can alter the observed magnitude and direction of these vectors.

36. What is a unit vector and why is it useful?

A unit vector is a vector with a magnitude of 1. It's useful because it allows us to specify direction without concern for magnitude. Unit vectors are often used as a basis for describing other vectors, making calculations and representations simpler.

37. How does the concept of vectors apply to forces?

Forces are vector quantities because they have both magnitude (strength) and direction. This allows us to accurately represent how forces act on objects, combine multiple forces using vector addition, and resolve forces into components for analysis.

38. What is the difference between collinear and parallel vectors?

Collinear vectors lie on the same line or are extensions of the same line, pointing either in the same or opposite directions. Parallel vectors have the same direction but may not lie on the same line. All collinear vectors are parallel, but not all parallel vectors are collinear.

39. How do you determine if two vectors are equal?

Two vectors are equal if and only if they have the same magnitude and direction. This means their components must be identical in all dimensions. Graphically, equal vectors would be represented by arrows of the same length pointing in the same direction.

40. What is the significance of vector decomposition in problem-solving?

Vector decomposition, or resolving a vector into its components, is crucial in problem-solving as it allows us to analyze complex motions or forces along simpler, often perpendicular directions. This simplifies calculations and helps in understanding the effects of vectors in different dimensions.

41. What is the importance of the commutative property in vector addition?

The commutative property in vector addition states that A + B = B + A, where A and B are vectors. This is important because it means the order in which we add vectors doesn't affect the result, simplifying many calculations and allowing flexibility in problem-solving approaches.

42. How do you interpret negative scalar quantities in physics?

Negative scalar quantities in physics often indicate a direction or change opposite to what is considered positive in the given context. For example, negative work means energy is being removed from a system, while negative acceleration means an object is slowing down if it was initially moving in the positive direction.

43. What is the physical significance of the magnitude of a vector?

The magnitude of a vector represents the size or strength of the quantity it describes, without regard to direction. For example, the magnitude of a velocity vector is the speed of the object, while the magnitude of a force vector is the strength of the force.

44. How do you determine if a physical quantity is a scalar or a vector?

To determine if a physical quantity is a scalar or vector, consider whether direction is necessary to fully describe it. If the quantity can be completely described by a single number and its units, it's a scalar. If it requires both a magnitude and a direction for a complete description, it's a vector.

45. What is the role of vectors in describing rotational motion?

Vectors play a crucial role in describing rotational motion. Angular velocity and angular acceleration are vector quantities, with their directions determined by the right-hand rule. Torque, which causes rotational acceleration, is also a vector quantity derived from the cross product of force and position vectors.

46. How does the concept of relative motion relate to vectors?

Relative motion is inherently related to vectors because it involves the difference between velocity vectors. When describing the motion of one object relative to another, we subtract the velocity vector of the reference object from the velocity vector of the object of interest.

47. What is the significance of the triangle law of vector addition?

The triangle law of vector addition is a graphical method for adding two vectors. It states that when two vectors are represented as two sides of a triangle taken in order, the resultant vector is represented by the third side of the triangle taken in the reverse order. This law provides a visual understanding of vector addition.

48. How do you interpret the result of a dot product between two vectors?

The dot product of two vectors results in a scalar quantity that represents how much the vectors are aligned with each other. A positive dot product means the vectors point in generally the same direction, a negative dot product means they point in generally opposite directions, and a zero dot product means they are perpendicular.

49. What is the difference between a vector field and a scalar field?

A scalar field assigns a scalar value to each point in space, such as a temperature distribution. A vector field assigns a vector to each point in space, such as a velocity field in fluid dynamics. Vector fields contain more information as they specify both magnitude and direction at each point.

50. How does the concept of vectors apply to electromagnetic fields?

Electromagnetic fields are described using vectors. The electric field (E) and magnetic field (B) are both vector quantities, having both magnitude and direction at each point in space. This vector nature is crucial for understanding how these fields interact with charged particles and with each other.

51. What is the physical interpretation of the cross product of two vectors?

The cross product of two vectors results in a vector perpendicular to both original vectors, with a magnitude equal to the area of the parallelogram formed by the two vectors. Physically, this can represent quantities like torque (cross product of force and position vectors) or angular momentum (cross product of position and linear momentum vectors).

52. How do you determine the direction of a resultant vector in 3D space?

The direction of a resultant vector in 3D space is determined by its components along the x, y, and z axes. If R is the resultant vector with components Rx, Ry, and Rz, its direction can be described by two angles: the azimuthal angle in the xy-plane (θ = tan^(-1)(Ry/Rx)) and the polar angle from the z-axis (φ = cos^(-1)(Rz/|R|)).

53. What is the significance of the parallelogram law of vector addition?

The parallelogram law of vector addition states that when two vectors are represented as adjacent sides of a parallelogram, their sum is represented by the diagonal of the parallelogram from their common point. This law provides a geometric interpretation of vector addition and is particularly useful in force diagrams.

54. How does the concept of vectors apply to quantum mechanics?

In quantum mechanics, vectors play a crucial role in describing the state of a system. The state vector, often denoted as |ψ⟩, is a vector in a complex vector space that contains all the information about the quantum system. Operators, which represent observable quantities, act on these state vectors.

55. What is the importance of understanding both scalar and vector quantities in physics?

Understanding both scalar and vector quantities is crucial in physics because it allows for a complete description of physical phenomena. Scalars provide magnitude information, while vectors provide both magnitude and direction. This distinction is essential for accurately analyzing and predicting the behavior of physical systems, from simple motions to complex field interactions.