Series RC Circuit

A Series RC circuit consists of a resistor (R) and a capacitor (C) connected in series, forming a fundamental component in electrical and electronic systems. When an AC voltage is applied, the circuit demonstrates unique behaviours in terms of charging and discharging the capacitor, as well as impedance. These characteristics are pivotal in various practical applications such as filtering signals, shaping waveforms, and timing circuits. In everyday life, series RC circuits are found in devices like audio equipment, where they help manage signal frequencies, and in-camera flashes, where they control the charging time of the flash capacitor. In this article, we will understand the dynamics of a Series RC circuit is essential for designing and optimizing electronic devices and systems.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Series RC Circuit
2. Important Points
3. Solved Examples Based on Series RC Circuit
4. Example 1: The susceptance of a circuit is
5. Summary

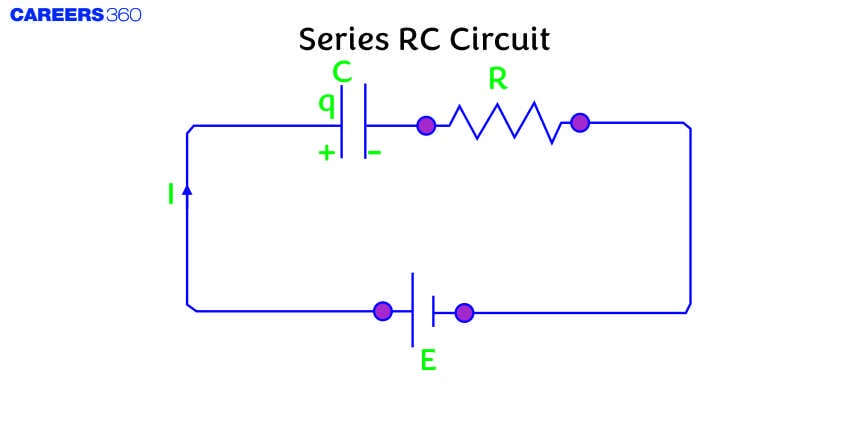
Series RC Circuit

A Series RC circuit is a simple electrical circuit that comprises a resistor (R) and a capacitor (C) connected in series with each other. This type of circuit is widely used in various electronic applications due to its ability to store and release energy, filter signals, and create time delays.

The above figure shows a circuit containing a resistor and capacitor connected in series through a sinusoidal voltage source voltage which is given by

$V=V_0 \sin (\omega t+\varphi)$

Now, in this case, the voltage across the resistor is V_R=IR

And, the voltage across the capacitor is

$V_c=\frac{I}{\omega C}$

As we have studied in the previous concept the V_R is in phase with current I and V_C lags behind I by a phase angle $90^{\circ}$

The above figure is the phase diagram of this case. So, the V is the resultant of $V_R$ and $V_C$. So we can write

$
\begin{aligned}
V & =\sqrt{V_R^2+V_C^2} \\
& =i \sqrt{R^2+\frac{1}{\omega^2 C^2}} \\
& =i Z
\end{aligned}
$
where,
$
\begin{gathered}
Z=\sqrt{R^2+\frac{1}{\omega^2 C^2}} \\
i=\frac{V}{Z}=\frac{V}{\sqrt{R^2+X_c^2}}=\frac{V}{\sqrt{R^2+\frac{1}{4 \pi^2 \nu^2 c^2}}}
\end{gathered}
$

Here, Z is the impedance of this circuit.

Now, from the phasors diagram, we can see that the applied voltage lags behind the current by a phase angle φ given by

Important Points

1. Capacitive susceptance $\left(S_C\right)$

Capacitive susceptance, denoted as B_C, is a measure of how easily an AC circuit with a capacitor can pass alternating current. It is the imaginary part of the admittance (Y) in an AC circuit, analogous to how resistance is the real part of the impedance. While impedance (Z) opposes the flow of current, susceptance facilitates it. In a capacitive circuit, susceptance is positive and is given by the reciprocal of capacitive reactance (X_C).

$\begin{aligned} & S_C=\frac{1}{X_c}=\omega C \\ & \omega C=2 \pi \nu C\end{aligned}$

2. Power factor

Power factor is a key parameter in electrical engineering that measures the efficiency of power usage in an AC electrical system. It is defined as the ratio of real power (P) to apparent power (S), where:

$
\text { Ratio }=\frac{\text { True Power }}{\text { Apprent power }}
$

So,
$
\cos \phi=\frac{R}{\sqrt{R^2+X_c^2}}
$

Recommended Topic Video

Solved Examples Based on Series RC Circuit

Example 1: The susceptance of a circuit is

1) $\frac{1}{R}$
2) $\frac{1}{Z}$
3) $\frac{1}{X}$
4) None

Solution:

Susceptance is a measure of how easy it is for alternating current to pass through a capacitance or an inductance. Susceptance is the imaginary part of admittance, whose real part is conductance, which is the inverse of resistance. So conductance, Susceptance, or Admittance, all have the same unit ohm^-1

Susceptance (S) -The reciprocal of reactance.

$S=\frac{1}{X}$

Hence, the answer is the option (3).

Example 2: Calculate the susceptance (S) in a given circuit.

1) $\frac{1}{\pi}$
2) $\frac{2}{\pi}$
3) $\pi$
4) $2 \pi

Solution:

Capacitive susceptance S_C

$\begin{aligned} & S_C=\frac{1}{X_c}=\omega L \\ & \omega L=2 \pi \nu C \\ & \text { Susceptance } S=\frac{1}{\text { rectance }}=\frac{1}{X_C} \\ & \begin{aligned} \therefore S & =\omega C \\ & =(2 \pi \times 50) \times 10^{-2} \\ & =\pi\end{aligned}\end{aligned}$

Hence, the answer is the option (3).

Example 3: For the LCR circuit, shown here, the current is observed to lead to the applied voltage. An additional capacitor C', when joined with the capacitor C present in the circuit, makes the power factor of the circuit unity. The capacitor C', must have been connected in :

1) series with C and has a magnitude $\frac{1-\omega^2 L C}{\omega^2 L}$
2) series with C and has a magnitude $\frac{C}{\left(\omega^2 L C-1\right)}$
3) parallel with C and has a magnitude $\frac{C}{\left(\omega^2 L C-1\right)}$
4) parallel with C and has a magnitude $\frac{1-\omega^2 L C}{\omega^2 L}$

Solution:

Power factor

The ratio of resistance and impedance $(\cos \phi)$.
After inserting $c /$ both become equal since
$
\cos \phi=\frac{R}{Z}=1
$
or $R^2=R^2+\left(X_L-X_C\right)^2$
$
=>X_L=X_C------2
$

This implies must reduced
This will happen when C is increased.
$\therefore C^{\prime}$ must be inserted in parallel to $C$.
$
\begin{aligned}
& \therefore \omega L=\frac{1}{\omega\left(C+C^{\prime}\right)} \\
& \text { or } C+C^{\prime}=\frac{1}{\omega^2 L \text { or }} C^{\prime}=\frac{1}{W^2 L}-C \\
& \text { or } C^{\prime}=\frac{1-\omega^2 L C}{\omega^2 L}
\end{aligned}
$

Hence, the answer is the option (4).

Example 4: Calculate the power factor for a given circuit

1) 0.012

2) 0.24

3) 0.028

4) 0.16

Solution:

Power factor

$
\cos \phi=\frac{R}{Z}
$
wherein
$
\begin{aligned}
& R \rightarrow \text { resistance } \\
& Z \rightarrow \text { impedance }
\end{aligned}
$

Power factor
$
\cos \phi=\frac{R}{Z}
$

In the given circuit

$\begin{aligned} & R=0.1 \Omega \\ & Z=\sqrt{R^2+\left(X_L-X_C\right)^2} \\ & X_L=\omega L=(2 \pi \times 50) \times 10^{-2}=\pi \\ & X_C=\frac{1}{\omega C}=\frac{1}{100 \pi \times 10^{-2}}=\frac{1}{\pi} \\ & Z=\sqrt{(0.1)^2+\left(\pi-\frac{1}{\pi}\right)^2}=8 \Omega \\ & \quad \Rightarrow \cos \phi=\frac{0.1}{8}=0.012\end{aligned}$

Hence, the answer is the option (1).

Example 5: Power factor is defined as the ratio of

$\begin{aligned} & \text { 1) } \frac{\text { Apparent Power }}{\text { True Power }} \\ & \text { 2) } \frac{\text { Instantaneous Power }}{\text { Apparent Power }} \\ & \text { 3) } \frac{\text { Instantaneous Power }}{\text { True Power }} \\ & \text { 4) } \frac{\text { True Power }}{\text { Apparent Power }}\end{aligned}$

Solution:

Power factor

$\begin{aligned} & \text { Ratio }=\frac{\text { True Power }}{\text { Apparent power }} \\ & \text { Power factor }=\frac{\text { True Power }}{\text { Apparent power }}\end{aligned}$

Hence, the answer is option (4).

Summary

A Series RC circuit, consisting of a resistor and a capacitor in series, is fundamental in various electronic applications due to its ability to filter signals, store and release energy, and create time delays. Key concepts include capacitive susceptance, which measures how easily an AC circuit with a capacitor passes alternating current, and power factor, which indicates the efficiency of power usage in an AC system. Understanding these principles helps in designing and optimizing electronic devices and systems, ensuring efficient power usage and performance.