Shear Modulus Elastic Moduli - Definition, Difference, FAQs

Edited By Team Careers360 | Updated on Jul 02, 2025 04:35 PM IST

What is the modulus of rigidity?

Elastic Shear modulus and elastic modulus: Moduli is a unit of modulus of rigidity of measurement for mechanical characteristics of solids. Young's modulus and bulk modulus are two other types of elastic moduli. Allow us to assist you in comprehending shear modulus and elastic modulus. The modulus of rigidity is also known as the shear modulus and elastic modulus of elasticity. Shear modulus and elastic modulus, also known as Modulus of rigidity, is the ratio of shear stress to shear strain. G is frequently used, but S or μ can also be used.

This Story also Contains

What is the modulus of rigidity?
What are elastic moduli?
What is Shear modulus and elastic modulus?
Difference between Modulus of rigidity and Modulus of Elasticity

Shear Modulus Elastic Moduli - Definition, Difference, FAQs

What are elastic moduli?

Elastic Moduli: An external force or load is necessary to modify the form or size of a body. Different materials with the same cross-section and length will deform differently when subjected to the same force. Knowledge of elastic properties of materials such as modulus of rigidity of steel, concrete, and others is crucial when constructing a structure since the elastic behaviour of materials plays an important part in the design. It's also used in the design of bridges, vehicles, ropeways, and other structures. A material with zero shear modulus and elastic modulus is one possible definition of a fluid.

A rigid body is an element with a distinct shape and form. All of the objects and shapes that we see around us are not totally rigid. These shapes can be bent, stretched, or compressed when an external force is applied. These shapes tend to distort when an external force is applied. The internal force that acts per unit area and is applied to restore the previous shape is known as stress. The ratio of the change in dimension caused to the original dimension of the body is characterized as a strain. The modulus of elasticity is the recognized relationship between stress and strain.

Also read -

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

What is Shear modulus and elastic modulus?

One of the measures of solids' mechanical properties is the shear modulus and elastic modulus of elasticity. Young's modulus and bulk modulus are two more elastomeric moduli.

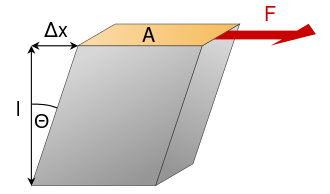
Shear modulus

A shear modulus and elastic modulus is used to describe a tiny deformation of a material caused by adding less shearing force and the ability of the material to restore to its previous state. However, the enormous sharing force is not suitable since it causes permanent deformations in the object.

Related Topics,

The dimensional modulus of rigidity formula for Shear modulus and elastic modulus is $M^1 L^{-1} T^{-2}$
The sign G is used to represent it.
It can be used to explain how a material resists transverse deformations, but only for tiny deformations that can be reversed. Large shearing pressures induce permanent deformations, which is why this is the case (no longer elastic body).

Material	values for shear modulus and elastic modulus (at room temperature)
Diamond	478.0
Modulus of rigidity of steel	79.3
Iron	52.5
Aluminium	25.5
Polyethylene	0.117
Copper	44.7
Titanium	41.4
Glass	26.2
Wood	4

NCERT Physics Notes:

Elastic Constants Relation

Young's Modulus, Bulk Modulus, as well as Shear modulus, and elastic modulus, are special formulations of Hooke's law, which asserts that strain experienced by corresponding stress applied is proportional to that stress in elastic material. As a result, the following equation can be used to represent the relationship between elastic constants:

$2 G(1+\nu)=E=3 K(1-2 \nu)$

Where,

The Shear modulus and elastic modulus are denoted by the letter G.

The Young's Modulus is denoted by the letter E.

The Bulk Modulus is K, while Poisson's Ratio is υ.

Difference between Modulus of rigidity and Modulus of Elasticity

Elasticity Modulus vs. Rigidity Modulus

The modulus of elasticity is defined as forces acting on the surface that are normal to it, whereas the modulus of rigidity is defined as the ratio of forces acting on the surface that are parallel to it laterally. The deformation for the modulus of elasticity is linear, but the deformation for the modulus of rigidity is circular. Only elastic deformations are affected by the modulus of elasticity, whereas non-elastic and elastic deformations are affected by the modulus of rigidity.

The object in the deforming force is either shortened or lengthened, depending on the modulus of elasticity; on the other hand, one of the object's surfaces is displaced relative to another surface, depending on the modulus of rigidity. The modulus of elasticity always exceeds the modulus of rigidity; the only exceptions are "auxetic" materials with negative Poisson's ratios, which are rare.

Also, check-

Frequently Asked Questions (FAQs)

1. What is elastic shear modulus and elastic modulus, and what does it mean?

The shear modulus and elastic modulus is a measure of a material's ability to resist transverse deformations and is only useful as an indicator of elastic behaviour for modest deformations after which the material can return to its original shape. Flow and permanent deformation or fractures are caused by large shearing pressures.

2. What is the SI unit of elasticity modulus?

The ratio of longitudinal stress and longitudinal strain is known as the modulus of elasticity. Because the strain has no unit, it will be represented by the stress unit. The Pascal is the SI unit for this modulus (Pa).

3. Is the modulus of rigidity of steel or aluminium more elastic?

Aluminium has a modulus of elasticity of 70 GPA, while the modulus of rigidity of steel has a modulus of 190–210 GPA. As a result of its higher Young modulus of elasticity, the modulus of rigidity of steel is more elastic than aluminium. As a result, aluminium has a higher rigidity than the modulus of rigidity of steel and is also more brittle.

4. What are the different kinds of elastic moduli?

Young's modulus, Shear modulus and elastic modulus, and Bulk modulus are the three forms of elastic moduli that exist.

5. How does the shear modulus differ from other elastic moduli?

The shear modulus specifically relates to a material's resistance to shear deformation, while other elastic moduli describe different types of deformation. For example, Young's modulus relates to tensile or compressive deformation, and the bulk modulus relates to volumetric deformation under uniform pressure.

6. Why is the shear modulus important in engineering and materials science?

The shear modulus is crucial for understanding how materials behave under various loading conditions. It helps engineers design structures that can withstand shear forces, such as bridges, buildings, and mechanical components. It's also important in predicting material failure and selecting appropriate materials for specific applications.

7. How does the shear modulus relate to a material's stiffness?

The shear modulus is directly related to a material's stiffness in response to shear forces. A higher shear modulus indicates greater stiffness and resistance to shear deformation. Materials with high shear moduli, like steel, are less likely to deform under shear stress compared to materials with low shear moduli, like rubber.

8. How is the shear modulus related to other elastic constants?

For isotropic materials, the shear modulus (G) is related to Young's modulus (E) and Poisson's ratio (ν) by the equation: G = E / [2(1 + ν)]. This relationship allows engineers to calculate one modulus if the others are known, providing a comprehensive understanding of a material's elastic properties.

9. What's the difference between isotropic and anisotropic materials in terms of shear modulus?

For isotropic materials, the shear modulus is the same in all directions. Anisotropic materials, however, have different shear moduli depending on the direction of applied stress. This difference is important in understanding how materials like wood or certain composites behave under various loading conditions.

10. What happens to the shear modulus near a material's melting point?

As a material approaches its melting point, its shear modulus typically decreases rapidly. This is because the material's structure becomes less rigid and more fluid-like, reducing its ability to resist shear deformation. At the melting point, the shear modulus effectively becomes zero as the material transitions to a liquid state.

11. What's the relationship between a material's shear modulus and its ability to transmit shear waves?

The shear modulus is directly related to a material's ability to transmit shear waves. The speed of shear waves (vs) in a material is given by vs = √(G/ρ), where G is the shear modulus and ρ is the density. Materials with higher shear moduli transmit shear waves faster, which is important in seismology and non-destructive testing.

12. What role does the shear modulus play in the phenomenon of buckling?

The shear modulus plays a significant role in buckling, especially for short columns or in the local buckling of thin-walled structures. While Euler buckling primarily depends on Young's modulus, shear deformation becomes important for shorter columns. The shear modulus affects the critical buckling load and the mode of failure, particularly in composite materials and sandwich structures.

13. What is the significance of the shear modulus in earthquake engineering?

The shear modulus is crucial in earthquake engineering because:

14. What is the relationship between a material's shear modulus and its ability to store elastic energy?

The shear modulus is directly related to a material's ability to store elastic energy under shear deformation. The elastic strain energy per unit volume (U) stored in a material under pure shear is given by U = τ²/(2G), where τ is the shear stress and G is the shear modulus. Materials with higher shear moduli can store more elastic energy for a given shear strain, which is important in applications like springs and energy-absorbing structures.

15. What is the shear modulus?

The shear modulus, also known as the modulus of rigidity, is a measure of a material's resistance to shear deformation. It quantifies how much a material resists changing shape when subjected to a shear stress (a force applied parallel to one of its surfaces while the opposite surface is fixed).

16. What is the mathematical definition of shear modulus?

The shear modulus (G) is defined as the ratio of shear stress (τ) to shear strain (γ): G = τ / γ. It represents the slope of the stress-strain curve in the elastic region for shear deformation.

17. Can you explain shear stress and shear strain in simple terms?

Shear stress is the force per unit area applied parallel to a surface, causing layers to slide past each other. Shear strain is the resulting deformation, measured as the angle of distortion. Imagine pushing the top of a deck of cards while holding the bottom still – that's shear.

18. Can the shear modulus be negative?

No, the shear modulus cannot be negative for stable materials. A negative shear modulus would imply that a material becomes less deformed as more stress is applied, which violates the principles of classical mechanics and material stability.

19. How does temperature affect the shear modulus?

Generally, the shear modulus decreases as temperature increases. This is because higher temperatures increase atomic vibrations and weaken interatomic bonds, making the material less resistant to shear deformation. The relationship between temperature and shear modulus is important in applications involving varying thermal conditions.

20. How does the shear modulus relate to a material's Poisson's ratio?

The shear modulus (G) is related to Poisson's ratio (ν) and Young's modulus (E) through the equation: G = E / [2(1 + ν)]. This relationship shows that:

21. How does the concept of shear modulus apply to fluids?

Fluids (liquids and gases) do not have a shear modulus in the same sense as solids. They cannot sustain a shear stress in static equilibrium. Instead, fluids are characterized by their viscosity, which describes their resistance to flow under applied stress. The concept of shear modulus is only applicable to solids or very viscous fluids over extremely short time scales.

22. What is the significance of the shear modulus in the study of material plasticity?

The shear modulus is significant in plasticity because:

23. What role does the shear modulus play in the phenomenon of acoustic metamaterials?

In acoustic metamaterials, the shear modulus is crucial because:

24. What role does the shear modulus play in the design of damping systems?

The shear modulus is important in damping system design because:

25. How is the shear modulus measured experimentally?

The shear modulus can be measured through various methods, including:

26. How does porosity affect a material's shear modulus?

Porosity generally decreases a material's shear modulus. As the volume fraction of pores increases, there's less solid material to resist shear deformation, leading to a lower overall shear modulus. The relationship is often non-linear, with small amounts of porosity having a disproportionately large effect on the shear modulus.

27. How does the shear modulus of a material change near absolute zero temperature?

As temperature approaches absolute zero:

28. How does the shear modulus of a material change during phase transformations?

During phase transformations:

29. How does the crystal structure of a material influence its shear modulus?

The crystal structure significantly affects a material's shear modulus. Materials with strong, directional bonds (like covalent or ionic bonds) tend to have higher shear moduli. The arrangement of atoms and the nature of their bonding determine how easily atomic planes can slide past each other under shear stress, directly influencing the shear modulus.

30. Why do some materials have a high Young's modulus but a low shear modulus?

This can occur in materials with anisotropic properties, where the resistance to deformation varies with direction. For example, certain composites might resist stretching (high Young's modulus) but be relatively weak against shearing forces (low shear modulus). This difference arises from the material's internal structure and the orientation of its reinforcing elements.

31. How does the shear modulus of metals compare to that of polymers?

Metals generally have much higher shear moduli than polymers. This is due to the strong metallic bonding in metals, which resists deformation more effectively than the weaker intermolecular forces in polymers. For example, steel might have a shear modulus around 80 GPa, while many polymers have shear moduli below 1 GPa.

32. Can a material's shear modulus change over time?

Yes, a material's shear modulus can change over time due to various factors:

33. How does work hardening affect a material's shear modulus?

Work hardening, or strain hardening, primarily affects a material's yield strength and ultimate strength, but it has minimal effect on the shear modulus. The shear modulus is an elastic property that describes behavior before yielding occurs. Work hardening changes the plastic behavior of a material but generally doesn't significantly alter its elastic properties, including the shear modulus.

34. Can you explain the concept of the complex shear modulus?

The complex shear modulus is used to describe the viscoelastic behavior of materials, particularly polymers. It consists of two parts:

35. How does the shear modulus of composite materials differ from that of their individual components?

The shear modulus of composite materials is often different from a simple average of its components' moduli. It depends on:

36. How does the concept of shear modulus apply to nanomaterials?

In nanomaterials, the concept of shear modulus becomes more complex:

37. What is the importance of the shear modulus in the study of material fatigue?

The shear modulus is important in fatigue studies because:

38. How does the presence of defects in a crystal structure affect its shear modulus?

Defects in a crystal structure can affect the shear modulus in several ways:

39. What is the relationship between a material's shear modulus and its fracture toughness?

The shear modulus and fracture toughness are related in several ways: