Shearing Stress - Definition, Meaning, Units, Formula, FAQs

Edited By Team Careers360 | Updated on Jul 02, 2025 05:06 PM IST

The internal resistance induced in a material per unit cross-sectional area when subjected to an external load is known as stress. Shear or shear stress in mechanics is the force generated due to the sliding of the one layer of object over the other. In simple term shear stress meaning or what is shear is the wearing of the material due to tangential forces applied per unit area. It is well known fact that when the load is applied on the any object it undergoes the deformation.

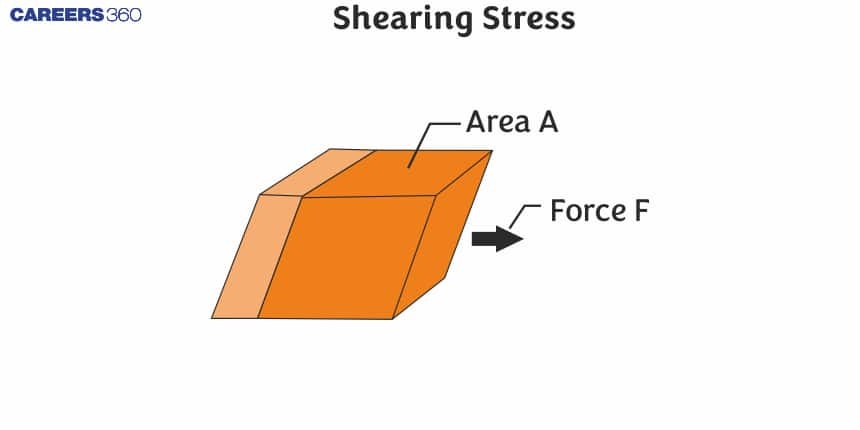
Shearing Stress - Definition, Meaning, Units, Formula, FAQs

When the force applied is in the direction of the plane of the object, the deformation of the object is along that plane. Due to this force object experiences the stress called as the shear stress or tangential stress. Shear stress induces the shear strain in material. Shear stress is denoted by Greek letter τ (tau). Its magnitude is calculated as the internal resistance (shear force) divided by the area resisting the shear force. The shear force definition is that the force that produces the tangential wear or tangential deformation in material is called as the shear force.

Shear stress definition?

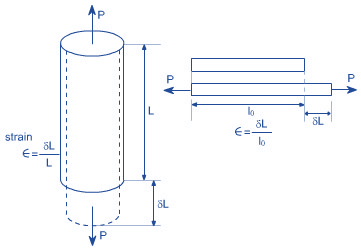
When a load is applied directly to the bar, the length of the bar (L) changes . The strain generated when the original length of the bar is L Changes by dLs and the ratio of the change in length to the original length is call as strain: Strain is thus a measure of material deformation and is a dimensionless quantity. That is, there are no units. It is simply the ratio of two quantities with the same unit.

1651125056625

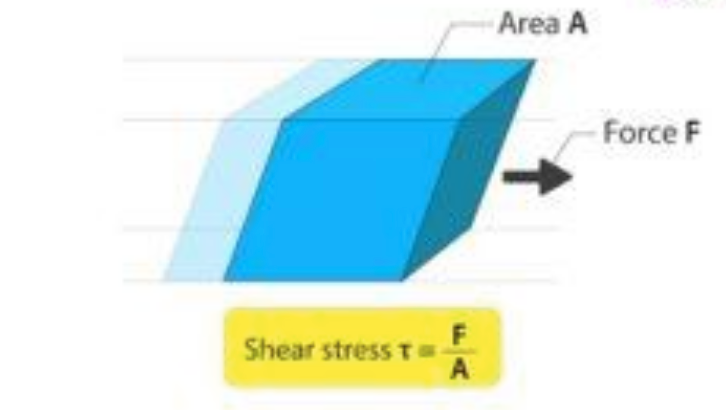
Shear Stress =Shear Force/Cross-Section Area

τ=F/A

It is also called shear force formula

Strain ϵ= δL/L Shear strain formula

Above equation is shear stress formula. Shear stress units or Shear stress unit is N/m²

Shear strain unit- dimensionless

Different Units of the Shear Stress

System of units	Stress units
Fundamental units	Kg.m-1.s-2
SI (derived units)	N/m2
SI (derived units)	Pa or pascal
SI (mm)(derived units)	M.Pa or N/(mm)2
US unit (ft)	lbf/ft2
US unit (inch)	Psi (lbf/inch2)

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Also read -

what is shear strain?

In simple term shear strain produces angle change in objects.

This shear deformation or slip can be defined as a change in right angles Or the angle of strain is called shear strain. Shear strain is measured in radians, so it is dimensionless, that is, it has no units.

Shear deformation is calculated as the displacement from the objects unique position of the surface in direct contact with the applied shear stress.

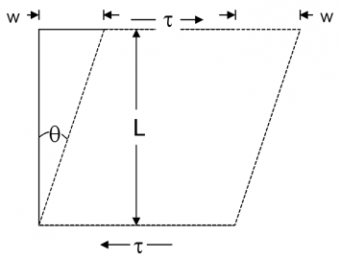
Shear strain

ϒ=wL = tanθ≈θ

Shearing Strain in Real Life

The second you awaken and move slowly at the mattress to get out of the mattress, until you move returned to sleep. Almost each example of the everyday pastime contains shear stress.

Some of such real-lifestyles situations are indexed below-

All types of Slicing and Cutting (Cutting fruits, vegetables, paper, cloth, tree etc)
Painting, Brushing, Applying creams/soaps/lotion/ointment etc. While Chewing meals among the teeth’s.
While strolling or strolling whilst our feet push floor returned to transport forward.
When a transferring automobile begins offevolved or stops, The floor of the seat revel in the shear stress.
When water flows River beds revel in shear stress.
Sometimes due to shear strain erosion may be noticed.
On the phone monitors whilst sliding.
While making ready Indian bread like Dosa, Roti, Pizza base etc.
Polishing the floor. Writing on blackboard with chalk piece On sliding etc.

Related Topics Link,

Material properties in shear – shear stress modulus

The relationship between shear stress and shear strain, and also between normal stress and axial deformation, is determined by experiments in labs.. Experiments show the linear characteristics of materials within elastic limit, the stress / strain ratio is determined by the expression:
τ= Gϒ
where G is the “modulus of shear “of the material. Note that shear modulus is in units of force per unit area (for example, lb / in² = psi and N / m² = Pa). The shear properties of linear elastic materials are closely related, in particular, the following relationship can be derived:
G = E /2(1+ v)
Here, E is Young's modulus and ν is the Poisson's ratio.

Stresses on Axially Loaded Members

Consider the stresses in an axially loaded bar with a cross-sectional area A. Here we will cut the bar perpendicular to the bar axis as shown below.

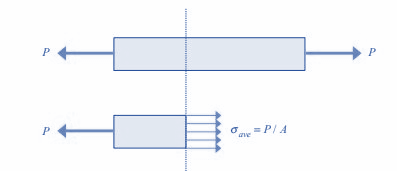
Stresses on Axially Loaded Members

Considering load P is acting on entire bar of length L , then it can be written as: σave = P / A where σave is average stress over the bar. In addition, due to the axial load perpendicular to the cross-section, the shear stress on the section is zero. Suppose we instead draw a line that goes through the bar at an angle θ, as shown in the following figure.

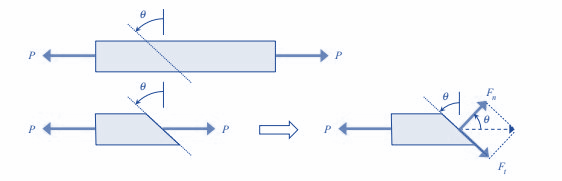
Shear stress

As a result of this cut, we see two important outcomes. First is that, the axial produced load has both normal and tangential part of the force on the cut face of:

Fn = Pcosθ

Ft = Psinθ

Other is that, the area of the cross section over which these resultant components act takes on the bigger value of area:

Ac = A/cosθ

With this, the part of the forces of stress normal and tangent to the cut can be written as :

σ= Fn/ Ac =Pcosθ A /cosθ = P/A cos² θ = P/2A(1+ cos2θ )

τ=Ft/Ac = P sinθ A /Cosθ = P/ACosθ Sinθ =P/2A Sin2θ

From this we see that the direction of the section of the element affects the values of the normal stress and shear stress components. In addition, we see that axial loads can create both shear and normal stress components. (Note that the highest shear stress occurs for the cut at θ = 45 °, where τ = P / 2A).

Also read :

Principal stresses and strains

The main planes are those planes within the material, so the resulting stresses through them are perfectly normal stresses or planes through which no shear stresses occur.
The principal stresses are the stresses that act on the principal planes.
The plane carrying the maximum normal stress is called the main principal plane and the stress acting on it is called the main principal stress.
The plane that bears a minimum normal stress is called the minor principal plane and the stress acting on it is called the minor principal stress.

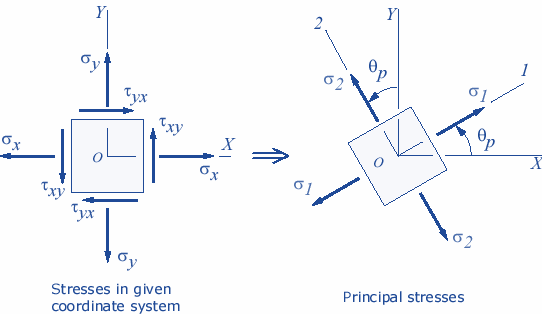
Principal stresses and strains

The angle ϴp where the shear stress τ_xy becomes zero.

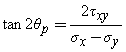
The angle ϴp can be defined in the principal directions where the only stresses are perpendicular stresses. These stresses generated at these angle are called principal stresses and they are found from the original stresses (expressed in the x,y,z directions) via. Below is the principle stress formula or principal stress formula:

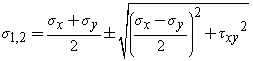
Another angle ϴs where the maximum shear stress occurs called as the maximum shear stress angle. This is found by finding the maximum of the shear stress transformation equation, and solving for ϴs. The result is,

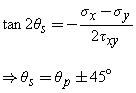
From above we can say that, the optimum shear stress is equal to half the difference between the two principal stresses,

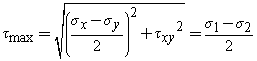
Maximum shear stress transformation can be illustrated as

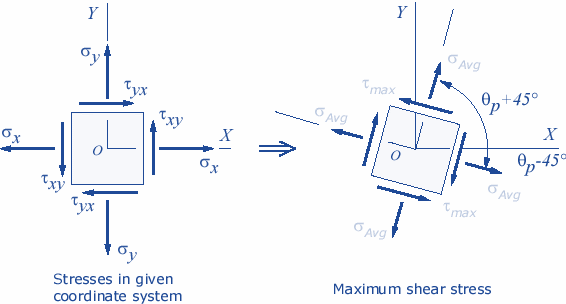
Maximum shear stress transformation

NCERT Physics Notes:

Shear Stresses in Fluids

Shear stresses in Newtonian fluids, a fluid at rest cannot resist shear (ideal fluids). Under the influence of force, it continuously deforms, no matter how small they may be. Resistance to shear forces in a fluid occurs only when the fluid is in motion. This implies the key difference between liquid and solid. For solids, the resistance to shear strain depends on the strain itself, i.e. the shear stress τ is depends on rate of shear strain γ. For liquids, shear stress is a function of strain rate dγ/dt. The property of a fluid to resist the development of shear strain is called viscosity.

The shape of the relationship between shear stress and strain rate depends on a fluid, and most common fluids obey Newton's law of viscosity, which states that shear stress is proportional to with strain rate:

τ =µ dγ/dt

Such a fluid is called a Newtonian fluid. The scaling factor µ is known as the dynamic viscosity and its value depends on the particular fluid. The dynamic viscosity divided by the density is called kinematic viscosity

ν = µ/ ρ

Also check-

Frequently Asked Questions (FAQs)

1. What is the unit of stress?

The unit of the stress is N/m2. It is defined as the internal resisting force per unit area.

2. What is strain?

Strain is the dimensional less quantity. It is defined as the ratio of the change in dimension to the original dimensions.

3. What is unit of the strain?

Strain is the ratio of two same quantities hence it is dimensionless.

4. What is Newton’s law of viscosity?

Newton’s law of viscosity gives the relationship between the shear stress and strain rate in fluids.

τ =µ dγ/dt

Where τ is shear stress and dγdt is rate of shear strain and µ is viscosity.

5. Write the formula for stress and strain?

Stress = Internal resisting force/crosssectional area

Strain = Change in dimension after deformation/Original Dimension

6. Define shear/ write shear definition.

The occurrence of shear strain is called shear.

7. What is shearing stress?

Shearing stress is the internal force acting parallel to the surface of a material when an external force is applied tangentially. It causes the layers of the material to slide over each other, resulting in deformation.

8. How does shearing stress differ from normal stress?

Shearing stress acts parallel to the surface of a material, while normal stress acts perpendicular to the surface. Shearing stress causes sliding deformation, whereas normal stress causes compression or tension.

9. What are the units of shearing stress?

The units of shearing stress are the same as those for pressure: Pascal (Pa) in the SI system, or pounds per square inch (psi) in the imperial system.

10. What is the formula for calculating shearing stress?

The formula for shearing stress is τ = F / A, where τ (tau) is the shearing stress, F is the force applied parallel to the surface, and A is the area over which the force is applied.

11. Can shearing stress exist without an external force?

No, shearing stress requires an external force applied tangentially to the surface of the material. Without an external force, there would be no internal forces causing the layers to slide.

12. What is shear strain, and how does it relate to shearing stress?

Shear strain is the deformation of a material resulting from shearing stress. It is measured as the angle of deformation and is directly proportional to shearing stress within the elastic limit of the material.

13. Why is understanding shearing stress important in engineering?

Understanding shearing stress is crucial in engineering for designing structures and components that can withstand various forces. It helps in predicting material behavior, preventing failures, and optimizing designs for strength and durability.

14. Can shearing stress cause material failure?

Yes, if the shearing stress exceeds the shear strength of the material, it can cause failure. This can result in deformation, cracking, or complete separation of the material along the plane of shear.

15. How does shearing stress relate to shear modulus?

Shear modulus (G) is a measure of a material's resistance to shearing deformation. It is defined as the ratio of shearing stress to shear strain: G = τ / γ, where τ is shearing stress and γ is shear strain.

16. How does shearing stress affect different materials?

Different materials respond to shearing stress differently based on their properties. Ductile materials may deform plastically under shear, while brittle materials might fracture. The response also depends on the magnitude of the stress and the material's shear strength.

17. What is the maximum shearing stress theory?

The maximum shearing stress theory, also known as Tresca's theory, states that yielding in a material begins when the maximum shearing stress in the material equals the shearing stress at yielding in a simple tension test.

18. How does grain structure in metals affect their response to shearing stress?

The grain structure of metals significantly influences their response to shearing stress. Finer grain structures generally provide greater resistance to shear deformation, while coarser grains may allow for easier slip along grain boundaries.

19. How does the principle of superposition apply to shearing stress?

The principle of superposition states that the total shearing stress in a material is the sum of individual shearing stresses caused by different loads, provided the material remains in the elastic range and deformations are small.

20. How does shearing stress contribute to the phenomenon of buckling in structures?

While buckling is primarily associated with compressive stress, shearing stress can play a significant role, especially in thin-walled structures. It can contribute to local buckling and affect the overall stability of the structure.

21. What is the difference between shearing stress and shear force?

Shearing stress is the internal force per unit area acting parallel to the surface, while shear force is the total force causing the shearing effect. Shearing stress is derived from the shear force divided by the area over which it acts.

22. How is shearing stress distributed in a beam?

In a beam, shearing stress is not uniformly distributed. It is typically zero at the top and bottom surfaces and reaches its maximum at the neutral axis. The distribution depends on the cross-sectional shape of the beam.

23. What is the relationship between shearing stress and bending moment in a beam?

Shearing stress in a beam is related to the rate of change of bending moment along the beam's length. The shear force, which causes shearing stress, is equal to the derivative of the bending moment with respect to the beam's length.

24. How does the cross-sectional area affect shearing stress?

The cross-sectional area is inversely proportional to shearing stress. For a given force, increasing the cross-sectional area decreases the shearing stress, while decreasing the area increases the stress.

25. How does temperature affect shearing stress in materials?

Temperature can significantly affect a material's response to shearing stress. Higher temperatures generally reduce a material's shear strength, making it more susceptible to deformation or failure under shearing stress.

26. What is the difference between elastic and plastic shear deformation?

Elastic shear deformation is reversible

27. How is shearing stress related to torsion?

Torsion creates shearing stress in a material. When a shaft is twisted, the shearing stress is distributed circularly around the shaft's cross-section, with the maximum stress occurring at the outer surface.

28. What is the significance of the yield point in relation to shearing stress?

The yield point is the stress level at which a material begins to deform plastically. For shearing stress, it represents the point beyond which the material will not return to its original shape when the stress is removed.

29. How does Poisson's ratio relate to shearing stress?

Poisson's ratio, which describes the ratio of transverse strain to axial strain, is related to shearing stress through the relationship between elastic constants. It affects how a material deforms under shear and other types of stress.

30. What is shear flow, and how is it related to shearing stress?

Shear flow is the shear force per unit length along a cross-section. It is related to shearing stress by the thickness of the material: shear flow divided by thickness equals shearing stress.

31. How does anisotropy affect shearing stress in materials?

Anisotropic materials have different properties in different directions. This means their response to shearing stress can vary depending on the direction of the applied force, leading to complex stress distributions and deformations.

32. What is the role of shearing stress in fluid mechanics?

In fluid mechanics, shearing stress is crucial in understanding fluid flow, especially for viscous fluids. It affects the velocity gradient in the fluid and is key to concepts like boundary layers and drag forces.

33. How does shearing stress contribute to fatigue failure?

Cyclic shearing stress can lead to fatigue failure in materials. Repeated application of shearing stress, even below the yield point, can cause microscopic cracks to form and propagate, eventually leading to material failure.

34. What is the relationship between shearing stress and Von Mises stress?

Von Mises stress is a combined stress metric that includes shearing stress components. It is used to predict yielding of materials under complex loading conditions and considers the contributions of normal and shearing stresses.

35. What is the importance of shearing stress in geotechnical engineering?

In geotechnical engineering, understanding shearing stress is crucial for analyzing soil stability, designing foundations, and predicting landslides. It helps in determining the shear strength of soils and their behavior under various loading conditions.

36. How does work hardening affect a material's response to shearing stress?

Work hardening increases a material's resistance to further deformation. As a material undergoes plastic deformation due to shearing stress, it becomes harder and more resistant to additional shearing, increasing its yield strength.

37. What is the relationship between shearing stress and shear viscosity in fluids?

Shear viscosity is the ratio of shearing stress to shear rate in a fluid. It describes a fluid's resistance to flow under shearing stress. Higher viscosity fluids require more shearing stress to achieve the same shear rate as lower viscosity fluids.

38. What is the significance of the shear center in beam theory?

The shear center is the point in a beam's cross-section through which a transverse force must act to produce no twisting. Understanding its location is crucial for analyzing and designing beams subject to shearing forces.

39. How does shearing stress contribute to the formation of slip bands in crystals?

Shearing stress can cause dislocations to move along slip planes in crystal structures. When many dislocations move along the same plane, they form visible slip bands, which are evidence of plastic deformation at the microscopic level.

40. What is the role of shearing stress in composite materials?

In composite materials, shearing stress is crucial in determining the strength of the interface between different components. It affects how loads are transferred between fibers and matrix, influencing the overall strength and failure modes of the composite.

41. How does shearing stress relate to the concept of shear lag in structural mechanics?

Shear lag describes the non-uniform stress distribution in wide flanges or plates. Shearing stress plays a key role in this phenomenon, as it transfers load from highly stressed regions to less stressed areas, affecting the overall stress distribution.

42. What is the importance of shearing stress in understanding earthquake mechanics?

Shearing stress is fundamental in earthquake mechanics. It builds up along fault lines due to tectonic movements and, when it exceeds the frictional resistance, causes sudden slips that result in earthquakes.

43. How does shearing stress contribute to the phenomenon of creep in materials?

Creep, the time-dependent deformation of materials under constant stress, can be influenced by shearing stress. Long-term exposure to shearing stress, even at levels below the yield strength, can cause gradual deformation in materials, especially at elevated temperatures.

44. What is the relationship between shearing stress and the strength of adhesive bonds?

The strength of adhesive bonds is often limited by their resistance to shearing stress. The shear strength of an adhesive bond is a critical factor in determining its overall effectiveness and durability in joining materials.

45. How does shearing stress affect the behavior of non-Newtonian fluids?

Non-Newtonian fluids exhibit complex responses to shearing stress. Their viscosity can change with the applied shear rate, leading to behaviors like shear thinning or shear thickening, which are not observed in Newtonian fluids.

46. What is the role of shearing stress in the process of metal forming?

Shearing stress is crucial in metal forming processes like forging, extrusion, and rolling. It causes plastic deformation of the metal, allowing it to be shaped into desired forms. Understanding shearing stress is key to optimizing these processes.

47. What is the significance of residual shearing stress in materials?

Residual shearing stress is stress that remains in a material after the external load is removed. It can significantly affect a material's properties and behavior, potentially leading to unexpected deformations or failures if not properly accounted for.

48. How does shearing stress relate to the concept of stress concentration?

Stress concentration occurs where there are abrupt changes in geometry, like holes or notches. These areas can experience significantly higher local shearing stresses compared to the average stress in the material, potentially leading to failure.

49. What is the importance of understanding shearing stress in biomechanics?

In biomechanics, shearing stress is crucial for understanding the behavior of biological tissues and structures. It plays a role in phenomena like blood flow dynamics, joint mechanics, and the response of tissues to mechanical loads.

50. How does shearing stress affect the properties of polymers?

Shearing stress can significantly influence polymer behavior. It can cause alignment of polymer chains, affecting properties like viscosity and strength. In some cases, it can lead to shear-induced crystallization or degradation of the polymer structure.

51. What is the relationship between shearing stress and friction?

Friction is closely related to shearing stress at the interface between two surfaces. The maximum static friction force is proportional to the normal force, with the coefficient of friction representing the ratio of shearing stress to normal stress at impending motion.

52. How does shearing stress contribute to the phenomenon of wear in materials?

Shearing stress plays a significant role in various wear mechanisms. It can cause surface fatigue, delamination, and abrasive wear by inducing local plastic deformation and material removal at contact points between surfaces.

53. What is the importance of shearing stress in the design of bolted joints?

In bolted joints, shearing stress is a critical consideration. The shear strength of the bolt material and the shearing stress at the interface between joined parts are key factors in determining the overall strength and reliability of the joint.

54. How does shearing stress affect the behavior of granular materials?

In granular materials like sand or powders, shearing stress influences the packing and flow behavior. It can cause dilatancy (volume increase under shear) or compaction, depending on the initial state and the magnitude of the stress.

55. What is the role of shearing stress in the formation of geological structures like folds and faults?

Shearing stress is fundamental in the formation of geological structures. It contributes to the bending and folding of rock layers, the development of fault planes, and the overall deformation of the Earth's crust over geological time scales.

56. How does shearing stress relate to the concept of yield surfaces in plasticity theory?

In plasticity theory, yield surfaces define the combination of stresses at which a material begins to yield. Shearing stress is a key component in many yield criteria, such as the von Mises and Tresca yield surfaces, which are used to predict material behavior under complex loading conditions.