Simple Harmonic Motion (S.H.M.) And Its Equation

Periodic motion characterises all simple harmonic motions. It moves back and forth between its extreme and mean positions, oscillating. The oscillating object experiences the restoring force throughout the oscillation. This restoring force is equivalent to the displacement from the object's mean position but has a direction that is opposite to that of the displacement.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Periodic Motion
2. General Equation of SHM
3. Differential equation of SHM:-
4. Graph of acceleration V/s time
5. Solved Examples Based on Simple Harmonic Motion (S.H.M.) And Its Equation
6. Summary
7. Frequently Asked Questions (FAQs):

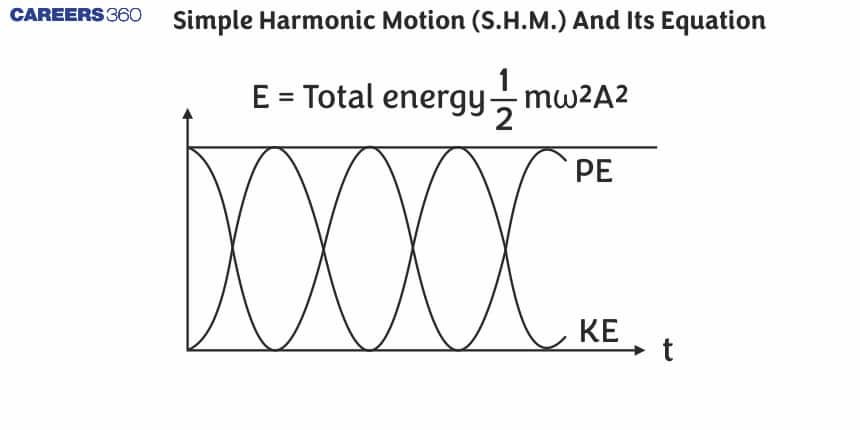
In this article, we will discuss the main concepts of Simple Harmonic Motion, as well as find its main formulas and discuss their use in different physical situations. At the same time, it helps them appreciate that S.H.M. is not just about passing exams but very beautiful and everywhere in nature. This topic falls under the broader category of Oscillations and Waves, which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, VITEEE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), more than thirty-five questions have been asked on this concept. and 3-4 questions in NEET from this concept.

Periodic Motion

Periodic motion is also called harmonic motion. Simple harmonic motion is the simplest form of oscillatory motion in which the particle oscillates on a straight line and the restoring force is always directed towards the mean position and its magnitude at any instant is directly proportional to the displacement of the particle from the mean position at that instant i.e. Restoring force α Displacement of the particle from the mean position.

$F=-kx\text{, where}\mathrm{x}\text{is measured from the mean position}$

Note: All oscillations are not simple harmonic motions but all simple harmonic motions are oscillatory motions.

Let’s understand SHM with the help of the spring block system:

Suppose we stretch the spring to the extreme position and then release it from there.

Here we can see that acceleration is always directed towards the mean position.

$\text{And}F=-kx$

$\text{Also,}a=\frac{F}{m}\Rightarrow a=-\frac{k}{m}x\Rightarrow a=-{\omega }^{2}x;\text{where}{\omega }^2\text{is a positive constant and}$

$\omega =\sqrt{\frac{k}{m}}\Rightarrow k=m{\omega }^2$

where k is a force or spring constant.

• v=0 at extreme position

• v=max at mean position

• a=0 at mean position

• $a=\text{max at extreme position, i.e., at}x=\pm A,a=\pm {\omega }^{2}A$

• $\text{Magnitude of maximum acceleration,}\left|a_{max}\right|={\omega }^{2}A$

As we know, $a=-{\omega }^{2}x$
$\Rightarrow \frac{dv}{dt}=-{\omega }^{2}x\Rightarrow v\frac{dv}{dx}=-{\omega }^{2}x\Rightarrow vdv=-{\omega }^{2}xdx$

Let the particle is released from an extreme position, i.e., at x=+A, v=0 and it becomes v when the displacement becomes x.

On integrating both sides of the above equation, we get:

$\begin{array}{rl}& {\int }_0^{v}vdv={\int }_A^x-{\omega }^{2}xdx\\ & \Rightarrow {\left[\frac{v^2}{2}\right]}_0^v=-{\omega }^2{\left[\frac{x^2}{2}\right]}_A^x\\ & \Rightarrow v^2-0=-{\omega }^2(x^2-A^2)\\ & \Rightarrow v^2={\omega }^2(A^2-x^2)\\ & \Rightarrow v=\pm \omega \sqrt{(A^2-x^2)}\\ & \text{At}x=0,v_{max}=\pm \omega A\end{array}$

Note:

As the relation between velocity (v) and position (x) in SHM is given by-

$v=\pm \omega \sqrt{(A^2-x^2)}$

This can be rearranged as

$\begin{array}{rl}& v^2={\omega }^2(A^2-x^2)\\ \Rightarrow & v^2={\omega }^2{A}^2-{\omega }^2{x}^2\\ \Rightarrow & v^2+{\omega }^2{x}^2={\omega }^2{A}^2\\ \Rightarrow & \frac{v^2}{{\omega }^2{A}^2}+\frac{x^2}{A^2}=1\end{array}$

This shows that the velocity-position graph is an ellipse (as shown in the below figure)

where,

Major axis=2A

and Minor axis =$2\omega A$

General Equation of SHM

1. For Displacement:

$x=\text{ASin}(wt+\varphi );\text{where}\varphi \text{is initial phase or epoch and}(\omega t+\varphi )\text{is called as phase.}$

Various displacement equations:-

(1) $x=$ ASinwt $\Rightarrow$ when particle starts from mean position towards right.
(2) $x=-$ ASinwt $\Rightarrow$ when particle starts from mean position towards left.
(3) $x=$ ACoswt $\Rightarrow$ when particle starts from right extreme position towards left
(4) $x=-$ ACoswt $\Rightarrow$ when particle starts from left extreme position towards Right.

2. For Velocity (v):

$\begin{array}{rl}x& =A\mathrm{Sin}(\omega t+\varphi )\\ \Rightarrow v& =\frac{dx}{dt}=A\omega \mathrm{Cos}(\omega t+\varphi )=A\omega \mathrm{Sin}(\omega t+\varphi +\frac{\pi }{2})\end{array}$

3. For Acceleration:

$\begin{array}{rl}x& =A\mathrm{Sin}(\omega t+\varphi )\\ \Rightarrow v& =\frac{dx}{dt}=A\omega \mathrm{Cos}(\omega t+\varphi )=A\omega \mathrm{Sin}(\omega t+\varphi +\frac{\pi }{2})\\ \Rightarrow a& =\frac{dv}{dt}=-A{\omega }^2\mathrm{Sin}(\omega t+\varphi )=A{\omega }^2\mathrm{Sin}(\omega t+\varphi +\pi )=-{\omega }^{2}x\end{array}$

So here we can see that the phase difference between x and v is $\frac{\pi }{2}$

similarly, the phase difference between v and a is $\frac{\pi }{2}$

similarly, the phase difference between a and x is $\pi$

Differential equation of SHM:-

$\begin{array}{rl}& \frac{dv}{dt}=-{\omega }^{2}x\\ & \Rightarrow \frac{d}{dt}\left(\frac{dx}{dt}\right)=-{\omega }^{2}x\\ & \Rightarrow \frac{d^{2}x}{d{t}^2}+{\omega }^{2}x=0\end{array}$

If the motion of any particle satisfies this equation then that particle will do SHM.

• Different graphs in SHM

$\text{For}x=a\mathrm{Sin}(\omega t)$

The Graph of Displacement v/s Time is Given as:

Graph of Velocity V/s Time

$v=a\omega \mathrm{Cos}(\omega t)$

Graph of acceleration V/s time

$\text{acceleration}=-a{\omega }^2\mathrm{Sin}(\omega t)$

Recommended Topic Video

Solved Examples Based on Simple Harmonic Motion (S.H.M.) And Its Equation

Example 1: A particle is moving with constant angular velocity along the circumference of a circle. Which of the following statements is true

1) The particle so moving executes SHM

2) The projection of the particle on any one of the tangents executes S.H.M

3) The projection of the particle on any one of the diameters executes SHM

4) None of the above

Solution:

Simple Harmonic Motion

It is a special case of the oscillatory motion of a vibrating particle in which the acceleration at any position is directly proportional to the displacement from the mean position & it is directed towards the mean position.

wherein

$\overrightarrow{a}\alpha -\overrightarrow{x}$

The projection of the particle on any of the diameters executes SHM

Hence, the answer is option (3).

Example 2: The motion which is not simple harmonic is

1) Vertical oscillations of a spring

2) Motion of a simple pendulum

3) Motion of a planet around the Sun

4) Vertical oscillation of a wooden plank floating in a liquid

Solution:

Simple Harmonic Motion

It is a special case of the oscillatory motion of a vibrating particle in which the acceleration at any position is directly proportional to the displacement from the mean position & it is directed towards the mean position.

wherein

$\overrightarrow{a}\alpha -\overrightarrow{x}$

The motion of a planet around the sun is a periodic motion but not a simple harmonic motion. All other given motions are examples of simple harmonic motion.

Example 3: If a simple harmonic motion is represented by $\frac{d^{2}x}{d{t}^2}+\alpha x=0$ its time period is:

1) $2\pi \alpha$
2) $2\pi \sqrt{\alpha }$
3) $2\pi /\alpha$
4) $2\pi /\sqrt{\alpha }$

Solution:

Equation of S.H.M.

$\begin{array}{rl}& a=-\frac{d^{2}x}{d{t}^2}=-w^{2}x\\ & w=\sqrt{\frac{k}{m}}\end{array}$
wherein
$x=A\sin (wt+\delta )$

The standard differential equation of SHM is

$\frac{d^{2}x}{d{t}^2}+{\omega }^{2}x=0$

The given equation is- $\frac{d^{2}x}{d{t}^2}+\alpha x=0$
$\begin{array}{rl}& \therefore {\omega }^2=\alpha \\ & \text{or}\omega =\sqrt{\alpha }\\ & \therefore T=\frac{2\pi }{\omega }=\frac{2\pi }{\sqrt{\alpha }}\end{array}$

Hence, the answer is the option (4).

Example 4: A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time.

1) at the highest position of the platform

2) at the mean position of the platform

3) for an amplitude of $\frac{g}{{\omega }^2}$
4) or an amplitude of $\frac{g^2}{{\omega }^2}$

Solution:

Equation of S.H.M. -

$\begin{array}{rl}& a=\frac{d^{2}x}{d{t}^2}=-w^{2}x\\ & w=\sqrt{\frac{k}{m}}\end{array}$
wherein
$x=A\sin (wt+\delta )$

In vertical simple harmonic motion, maximum acceleration $\left(A{\omega }^2\right)$ and so the maximum force $\left(mA{\omega }^2\right)$ will be at extreme positions. At the highest position, the force will be towards the mean position and so it will be downwards. At the lowest position, the force will be towards the mean position and so it will be upwards This is opposite to the weight direction of the coin.

1. At the lowest position-

$\mathrm{N}-\mathrm{mg}=\mathrm{ma}$
$\begin{array}{rl}& \Rightarrow \mathrm{N}=\mathrm{mg}+\mathrm{ma}\\ & \because N\ne 0\end{array}$

Case 2. At the highest position-

mg-N=ma

N=ma-mg

For loss of contact, N=

ma=mg

$\begin{array}{r}a=g\Rightarrow w^{2}x=g\\ \Rightarrow x=\frac{g}{w^2}\end{array}$

At the highest position $x=x_{max}=A$

Loss of contact will occur for amplitude $A=\frac{g}{w^2}$ at the highest point of the platform.

The coin will leave contact at any point when the acceleration of the platform is more than ′g′ and in the same direction of ′g′. At the highest point, both of the conditions are satisfied.

Hence, the answer is the option(3).

Example 5: The displacement of a particle varies according to the relation $x=4(\cos \pi t+\sin \pi t)$. The amplitude of the particle is $n\sqrt{2}$. find ' $n$ '.

1) 4

2) 2

3) 3

4) 8

Solution:

Equation of S.H.M.-

$\begin{array}{rl}& a=-\frac{d^{2}x}{d{t}^2}=-w^{2}x\\ & x=A\sin (wt+\delta )\\ & :x=4(\cos \pi t+\sin \pi t)\\ & =4\times \sqrt{2}[\frac{1}{\sqrt{2}}\cos \pi t+\frac{1}{\sqrt{2}}\sin \pi t]\\ & \text{or}x=4\sqrt{2}[\sin \frac{\pi }{4}\cos \pi t+\cos \frac{\pi }{4}\sin \pi t]\\ & =4\sqrt{2}\sin (\pi t+\frac{\pi }{4})\end{array}$

Hence amplitude $=4\sqrt{2}$

Hence, the answer is option (1).

Summary

Simple harmonic motion is characterized by the fact that if the particle is displaced from the equilibrium point, then acceleration will be proportional to displacement. This motion shows oscillatory nature and we can see various types of oscillations around us always.

Frequently Asked Questions (FAQs):

Q 1: The restoring force of SHM is maximum when the particle

Ans: Simple Harmonic Motion - It is a special case of the oscillatory motion of a vibrating particle in which the acceleration at any position is directly proportional to the displacement from the mean position & it is directed towards the mean position.

Q 2: What is constant in SHM?

Ans: An Oscillation is a special type of periodic motion in which a particle moves to and fro about a fixed point called the mean position of the particle.

Q 3: Which of the following is a necessary and sufficient condition for SHM?

Ans: Mean Position: A position during oscillation where the particle is at the equilibrium position, i.e. net force on the particle at this position is zero.

wherein Force acting on particles always points towards the mean position.

Q 4: Give the example of periodic motion.

Ans: Circular motion with uniform speed.

Q 5: What is Osillation?

Ans: An Oscillation is a special type of periodic motion in which a particle moves to and fro about a fixed point called the mean position of the particle.