Spring Force

Spring is a tool used daily by many of us and its inertia is frequently neglected by assuming it is massless. When a spring is compressed or extended by an external force, a restoring force is generated. This force is usually proportional to the compression or elongation (for small displacements). The spring force F is written as F = – k x where x is the displacement and k is the force constant. The negative sign denotes that the force is opposite to the displacement from the unstretched state.

This Story also Contains

1. What is Spring force?
2. Combination of Spring
3. Solved Examples Based on Spring Force
4. Summary

In this article, we will cover the concept of spring force. This topic falls under the broader category of laws of motion, which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), almost five questions have been asked on this concept. And for NEET one question was asked from this concept.

Let's read this entire article to gain an in-depth understanding of spring force.

What is Spring force?

The spring force is the restorative force exerted by a spring when stretched or compressed. It is proportional to the displacement from its relaxed length, but in the opposite direction.

Spring force is given by

$F_{s p}=-k \Delta x$

where,

F_sp = spring force

k = spring constant

Δx = net elongation or compression in the spring

Force at every point in a massless spring remains the same, so we can solve questions of spring by considering it as string and spring force as tension.

Spring Constant

$k \alpha \frac{1}{l}$

Where, k=spring constant

l=length of spring

Combination of Spring

There are mainly two types of combinations of spring which are listed below:

• Series Combination

$\frac{1}{k_{e q}}=\frac{1}{k_1}+\frac{1}{k_2}$

• Parallel Combination

$k_{e q}=k_1+k_2$

For More Information On Spring Force, Watch The Below Video:

Solved Examples Based on Spring Force

Example 1: A spring hanging from the ceiling of an elevator has a spring constant of 60N/m and a block attached to the other end with a mass of 5kg. If the elevator is accelerating upward at a rate of 3m/s2 and the spring is in equilibrium, what is the displacement of the spring? (in meters)

1) 1.08

2) 0.67

3) 2.24

4) 1.54

Solution:

Spring force is given by

$F_{s p}=-k \Delta x$

where,

F_sp=spring force

k= spring constant

Δx=net elongation or compression in the spring

By using this concept, let us solve this problem -

Since the displacement of the spring is at equilibrium, we can write:

$F_{\text {net }}=0$

There are three forces we can account for spring force, gravitational force, and the additional force resulting from the acceleration of the elevator. If we assume that forces pointing upward are positive, we can write:

$F_{\text {spring }}-F_g-F_e=0$

Substituting expressions for each force, we get:

$k x-m g-m a=0$

Rearrange to solve for displacement:

$x=\frac{m(g+a)}{k}=\frac{5(10+3)}{60}=1.08 \mathrm{~m}$

Hence, the answer is option (1).

Example 2: Consider the following system:

Both springs have a constant of 25N/m and the block is motionless. If the bottom spring is compressed 0.4m past its equilibrium and the block has a mass of 3kg, how far is the top spring stretched past its equilibrium? (answer in meters)

1) 0.8

2) 0.4

3) 0.6

4) 1

Solution :

By using this combination of spring concepts, let us solve this problem -

Since the block is motionless, we know that our forces will cancel out:

$\therefore F_{\text {net }}=0$

There are three forces in play: one from each spring, as well as the force of gravity. If we assume that forces pointing up are positive, we can write:

$F_{\text {spring.top }}+F_{\text {spring.bot }}-m g=0$

Plugging in expressions for each spring force, we get:

$k x_{\text {top }}+k x_{b o t}-m g=0$

Rearranging for the displacement of the top spring, we get:

$x_{\text {top }}=\frac{m g-k x_{b o t}}{k}=\frac{(3 k g)\left(10 m / s^2\right)-(25 \mathrm{~N} / \mathrm{m})(0.4 \mathrm{~m})}{25 \mathrm{~N} / \mathrm{m}}=0.8 \mathrm{~m}$

Hence, the answer is option (4).

Example 3: A Particle of mass 0.3 kg is attached to an ideal spring of spring constant $k=15 \mathrm{~N} / \mathrm{m}$, What will be the acceleration (in $\mathrm{m} / \mathrm{s}^2$ ) of the particle if it is released from a position when the elongation of the spring is 20 cm.

1) 10

2) 5

3) 3

4) 15

Solution :

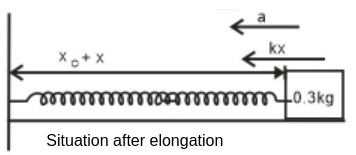
Given,
$
\begin{aligned}
& k=15 \mathrm{~N} / \mathrm{m}^2 \\
& \Delta x=20 \mathrm{~cm}=0.2 \mathrm{~m}
\end{aligned}
$

Spring force, $(F)=k \Delta x$
$
F=15 \times 0.2=3 N \ldots(1)
$

From Newton's 2nd Law-
$
\begin{aligned}
& F_{\text {net }}=m a \\
& \Rightarrow F=m a=0.3 a \ldots
\end{aligned}
$

From equation (1) and (2), We get
$
\begin{aligned}
0.3 a & =3 \\
\Rightarrow a & =10 \mathrm{~m} / \mathrm{s}^2
\end{aligned}
$

Hence, the answer is option (1).

Example 4: A spring whose unstretched length is I has a force constant $k$. The spring is cut into two pieces of unstretched lengths $l_1$ and $l_2$ where, $l_1=n l_2$ and n is an integer. The ratio $k_1 / k_2$ of the corresponding force constants, $k_1$ and $k_2$ will be:
1) $n$
2) $\frac{1}{n^2}$
3) $\frac{1}{n}$
4) $n^2$

Solution:

$\begin{aligned} & \text { Here, } \mathrm{I}_1+\mathrm{I}_2=\mathrm{I} \text { and } \mathrm{I}_1=\mathrm{nl}_2 \\ & k_1 l_1=k_2 l_2=k l \\ & \frac{k_1}{k_2}=\frac{l_2}{l_1}=\frac{l_2}{n l_2}=\frac{1}{n} \quad\left(l_1=n l_2\right)\end{aligned}$

Hence, the answer is option (3).

Example 5: A particle of mass $m$ is fixed to one end of a light spring having force constant k and unstretched length l . The other end is fixed. The system is given an angular speed $\omega$ about the fixed end of the spring such that it rotates in a circle in gravity-free space. Then the stretch in the spring is :

1) $\frac{m l \omega^2}{k-\omega m}$
2) $\frac{m l \omega^2}{k-m \omega^2}$
3) $\frac{m l \omega^2}{k+m \omega^2}$
4) $\frac{m l \omega^2}{k+m \omega}$

Solution:

As natural lentgh=1
Let elongation $=\mathrm{x}$
Mass $m$ is moving with angular velocity $\omega$ in a radius $r$
where $r=l+x$
Due to elongation x spring force is given by $F_s=K x$
And $F_C=m \omega^2 r=m \omega^2(l+x)$
as $F_C=F_s$
So
$
\begin{aligned}
& K x=m \omega^2(l+x) \\
\Rightarrow & x=\frac{m \omega^2 l}{K-m \omega^2}
\end{aligned}
$

Hence, the answer is option (2).

Summary

This article concludes with brief interesting information about the spring force, spring force formula, and combination of springs. It also discusses the examples of spring force used in everyday life for smoothing the working of the equipment. It also discusses the derivation of the combination of springs. This article tried to give a better understanding of the concept of spring force and an example of spring with clarity in an elaborate manner.