Standing Wave On A String

Standing waves on a string are fascinating phenomena observed when waves travelling in opposite directions on the string interfere, creating stationary patterns of oscillation. Imagine plucking a guitar string—the resulting vibration produces specific notes due to the formation of standing waves. These waves occur when the frequency of vibration matches the natural frequencies of the string, leading to points of maximum and minimum motion, known as antinodes and nodes, respectively. In real life, standing waves are not just limited to musical instruments; they are also seen in bridges, tall buildings, and even in everyday objects like swings, where certain conditions create stable oscillatory patterns.

This Story also Contains

1. What are Standing Waves?
2. What are Nodes and Antinodes?
3. Standing Wave in a String Fixed at Both Ends
4. Standing Wave in a String Fixed at One End
5. Solved Examples Based on Standing Wave on A String
6. Summary

What are Standing Waves?

When two sets of progressive waves of the same type (both longitudinal or both transverse) having the same amplitude and same time period or frequency or wavelength travelling along the same straight line with the same speed in opposite directions superimpose, a new set of waves are formed. These are called stationary waves.

Some of the Characteristics of Standing Waves

(1) In this the disturbance is confined to a particular region between the starting point and the reflecting point of the wave.
(2) In this there is no forward motion of the disturbance from one particle to the adjoining particle and so on, beyond this particular region.
(3) The total energy in stationary waves is twice the energy of each incident and reflected wave. But there is no flow or transfer of energy along the stationary wave.
(4) Points in a standing wave, which are permanently at rest. These are called nodes. The distance between two consecutive nodes is $\frac{\lambda }{2}$

(5) The Points on the standing wave having maximum amplitude are known as antinodes. The distance between two consecutive antinodes is also $\frac{\lambda }{2}$
(6) All the particles execute simple harmonic motion about their mean position (except those at nodes) within the same time period.

Note - In standing waves, if the amplitude of component waves is not equal. The resultant amplitude at nodes will not be zero. It will be a minimum. Because of this, some energy will pass across nodes and waves will be partially standing.

Let us take an example to understand and derive the equation of standing wave

Let us take a string and when a string is under tension and set into vibration, transverse harmonic waves propagate along its length. If the length of the string is fixed, reflected waves will also exist. These incident and reflected waves will superimpose to produce transverse stationary waves in a string

Incident wave $y_1=a\sin \frac{2\pi }{\lambda }(vt+x)$
Reflected wave $y_2=a\sin \frac{2\pi }{\lambda }[(vt-x)+\pi ]=-a\sin \frac{2\pi }{\lambda }(vt-x)$

Now we can apply the principle of superposition to this and get

$y=y_1+y_2=2a\cos \frac{2\pi vt}{\lambda }\sin \frac{2\pi x}{\lambda }$

So, $y=(2A\sin kx)\cos \omega t$
So, it can be written as - $y=R\cos \omega t$...... (1) where, $R=2A\sin kx\dots \dots$ (2)

Equation (1) and (2) shows that after the superposition of the two waves, the medium particle executes SHM with the same frequency and amplitude. Thus on the superposition of two waves travelling in opposite directions, the resulting interference pattern will form Stationary waves.

What are Nodes and Antinodes?

Nodes and antinodes are key concepts in the study of standing waves, which are waves that appear to be stationary rather than travelling through a medium.

• Nodes are points along a standing wave where the wave has minimal or no displacement. At these points, the destructive interference between the two opposing waves results in zero amplitude, meaning the medium (like a string or air) does not move at all at these locations. Nodes are evenly spaced along the wave and are crucial in defining the wave's structure.

• Antinodes, on the other hand, are points where the wave reaches its maximum displacement. At these locations, the constructive interference of the waves results in the maximum amplitude, causing the medium to oscillate with the greatest intensity. Antinodes are also evenly spaced, appearing midway between nodes.

Points in a standing wave, which are permanently at rest. These are called nodes. The Points on the standing wave having maximum amplitude is known as antinodes.

For nodes

From equation (2) we can say that $-kx=n\pi$

So, $x=\frac{n\pi }{k}=\frac{n\pi }{\frac{2\pi }{\lambda }}=\frac{n\lambda }{2}$

So, at the point where $x=0,\frac{\lambda }{2},\lambda \dots$ displacement is zero

For antinodes

From equation (2) we can say that $kx=(2n+1)\frac{\pi }{2}$

So, $x=(2n+1)\frac{\lambda }{4}$

So, again using equation (2) $y=\pm 2A$

Thus at the point at which $x=\frac{\lambda }{4},\frac{3\lambda }{4},\frac{5\lambda }{4}\dots ..$, displacemnet is maximum $(\pm 2A)$

Standing Wave in a String Fixed at Both Ends

As we know a string is said to vibrate if it vibrates according to the given equation

$y=(2A\sin kx)\cos \omega t$

From this equation, for a point to be a node,

$x=\frac{n\lambda }{2}$, where $n=0,1,2,3,\dots$.

In this, the string is fixed at both ends, so these ends are nodes. So, for $x=0$ and for $x=L$ (which will be a node). So, it can be written as

$L=\frac{n\lambda }{2}$, or, $\lambda =\frac{2L}{n}$ where $n=1,2,3,\dots$

So, the corresponding frequencies will be

$f=\frac{v}{\lambda }=n\left(\frac{v}{2L}\right)$, where $n=1,2,3\dots$

here, $v$ = speed of travelling waves on the string

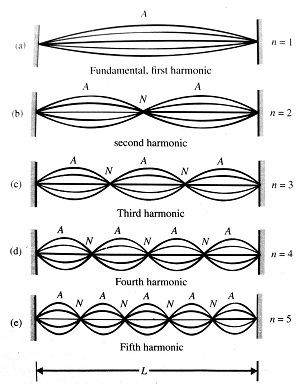
In the above figure we can see that by putting the values of 'n', we are getting different frequencies. For example

1. for $n=1,f=\frac{v}{2L}$ and it is called fundamental frequency or first harmonic.

The corresponding mode is called the fundamental mode of vibration.

2. If $n=2,f_1=2\left(\frac{v}{2L}\right)=\frac{v}{L}$
This second harmonic or first overtone and $f_1=2f$

Similar to this, we can increase the value of 'n' and we get the respective harmonic and overtone.

Now, the velocity of the wave in the string is given by

$\nu =\sqrt{\frac{T}{\mu }}$

So the natural frequency can be written as$f_n=\frac{n}{2L}\sqrt{\frac{T}{\mu }};n=1,2,3,\dots$

Standing Wave in a String Fixed at One End

In this case, one end is fixed and the other end is free. In the fundamental mode, the free end is an antinode, the length of the string

$L=\frac{\lambda }{4}$

So, in the next mode

$L=\frac{3\lambda }{4}$

So, in general, we can write the equation

$L=\frac{n\lambda }{4},n=1,3,5\dots$

From this, we can write the resonance frequency

$f_n=n\frac{v}{4L}=n{f}_1;n=1,3,5,\dots$

where, $f_{1=}=\frac{v}{4L}$ (Fundamental frequency)

Solved Examples Based on Standing Wave on A String

Example 1: In stationary wave

1) Strain is maximum at nodes

2) Strain is maximum at antinodes

3) Strain is minimum at nodes

4) amplitude is zero at all points

Solution:

Standing wave

Two identical waves travel in opposite directions in the same medium and combine to form a stationary ave

At nodes pressure changes so, strain is maximum

Hence, the answer is the option (1).

Example 2: The phase difference between the two particles situated on both sides of a node is

1) $0^\circ$

2) $90^\circ$

3) $180^\circ$

4) $360^\circ$

Solution:

Standing wave

Two identical waves travel in opposite directions in the same medium and combine to form a stationary wave.

All the particles vibrating in a given loop are in the same phase and particles in two consecutive loops are in opposite phases to each other.

So two particles situated on both the sides of node will be in opposite phases of vibration since they correspond to different but consecutive loops

Hence, the answer is the option (3).

Example 3: Equation $y=0.15\sin 5x\cos 300t$ describes a stationary wave. The wavelength of a stationary wave is

1) 1.256

2) 0

3) 2.512

4) 0.62

Solution:

Equation of stationary waves

$\begin{array}{rl}& y_1=A\sin (kx-\omega t)\\ & y_2=A\sin (kx+\omega t)\end{array}$

wherein

Resultant wave

$y=(2A\sin kx\cdot \cos \omega t)$

Compared with the standard equation
$\frac{2\pi }{\lambda }=5\Rightarrow \lambda =\frac{6.28}{5}=1.256\mathrm{m}$

Hence, the answer is the option (1).

Example 4: Equation $y=5\sin \frac{\pi x}{3}\cos 40\pi t$ is given. Find the separation (in cm) between two adjacent node

1) 3

2) 1.5

3) 6

4) 4

Solution:

$\begin{array}{rl}& y_1=A\sin (kx-\omega t)\\ & y_2=A\sin (kx+\omega t)\end{array}$
wherein
Resultant wave
$y=(2A\sin kx\cdot \cos \omega t)$

From comparison
$\begin{array}{rl}& \frac{2\pi X}{\lambda }=\frac{\pi X}{3}\\ \Rightarrow & \lambda =6\end{array}$
so distance is $\frac{\lambda }{2}=3\mathrm{cm}$

Hence, the answer is the option (3).

Example 5: If you step up the seventh harmonic on a string fixed at both ends, how many nodes and antinodes are set up in it

1) 8, 7

2) 7, 7

3) 8, 9

4) 9, 8

Solution:

A node in a standing wave

The position at which the amplitude of oscillation has zero value is called node.

wherein

At nodes

$\begin{array}{rl}& \sin kx=0\\ & kx=0,\pi ,2\pi \dots \dots n\pi \end{array}$
7th harmonic means 7 loops
In one loop [ 2nodes, 1 antinodes]
so in 7 loop
8 nodes and 7 antinodes will be there

Hence, the answer is the option (1).

Summary

Standing waves on a string occurs when two identical waves travel in opposite directions and interfere, creating stationary patterns with nodes (points of no displacement) and antinodes (points of maximum displacement). These waves are characterized by the absence of energy transfer along the wave and the formation of specific harmonic frequencies. Understanding these principles helps explain phenomena in various physical systems, including musical instruments and structural vibrations.