Sticking Of A Block With Accelerated Cart

When driving on a level road, most drivers assume that their vehicles will maintain control and stability. However, skidding, a situation where a vehicle loses traction and slides uncontrollably, can occur even on flat surfaces. Skidding is often caused by factors such as sudden braking, sharp turns, or wet and slippery road conditions. In real life, skidding can lead to dangerous situations, especially if the driver panics or is unprepared. For example, a driver may suddenly brake to avoid a pedestrian, but if the road is wet, the vehicle might skid and lose control, potentially leading to an accident. Understanding the causes and prevention of skidding is crucial for safe driving.

Skidding of Vehicle on a Level Road

While solving with the help of the concept of pseudo-force.

When a cart moves with some acceleration toward the right then a pseudo force (ma) acts on the block toward the left.

This force (ma) is an action force by a block on the cart.

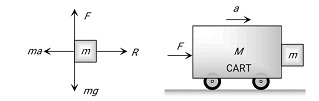
Now block will remain static w.r.t.cart. If friction force = μ_R ≥ mg

For equilibrium condition
$
\begin{aligned}
& \mu m a \geq m g \\
& a \geq \frac{g}{\mu} \\
& \mathrm{R}=\mathrm{ma} \\
& \therefore \quad a_{\min }=\frac{g}{\mu}
\end{aligned}
$
So, minimum force is applied on the cart so that the block will remain static w.r.t.cart.

$
F_{\min }=(M+m) \frac{g}{\mu}
$

where
$F_{\text {min }}=$ Minimum force
$a_{\text {min }}=$ minimum acceleration cart

M, m are masses of the cart and block respectively

Recommended Topic Video

Solved Examples Based on Skidding of Vehicle on A Level Road

Example 1: As shown here, in the figure, a cart C with mass M moves with acceleration 'b'. If the coefficient of friction between block A having mass m and the cart is μ, then, the acceleration of the cart and block system is independent of:

1) g

2) M

3) m

4) Both b) and c)

Solution:

If the cart is accelerated with 'b'

Pseudo force on the mass $F=m \times b=m \cdot b$
The force of friction $=\mu \mathrm{N}$
For horizontal equilibrium $\mathrm{F}=\mathrm{N}$
$f=\mu \mathrm{mb}$
The block will not fall as long as $\mathrm{f} \geq \mathrm{mg}$
$\mu \mathrm{mb} \geq \mathrm{mg}$
$\mathrm{b} \geq \mathrm{g} / \mu$

Hence, the answer is the option (4).

Example 2: As shown here, in the figure, cart C moving with acceleration 'b'. If the coefficient of friction between block A and the cart is $\mu$ then what is the maximum value of 'b' so that block A does not fall?

1) $\mu g$
2) $\mu^2 g$
3) $\frac{g}{\mu} $
4) None of these

Solution:

Sticking of a Block With Accelerated Cart

While solving with the help of the concept of pseudo-force.

When a cart moves with some acceleration toward the right then a pseudo force (ma) acts on the block toward the left.

This force (ma) is an action force by a block on the cart.

Now block will remain static w.r.t. block. If friction force= μR≥mg

For equilibrium condition

$\begin{aligned} & \mu m a \geq m g \\ & a \geq \frac{g}{\mu} \\ & \mathrm{R}=\mathrm{ma} \\ & \therefore \quad a_{\min }=\frac{g}{\mu} \\ & \quad F_{\min }=(M+m) \frac{g}{\mu}\end{aligned}$

Pseudo force (ma) acts on block towards the left
$
\begin{aligned}
& F_{\min }=\text { Minimum force } \\
& a_{\min }=\text { minimum acceleration cart }
\end{aligned}
$

$\mathrm{M}, \mathrm{m}$ are masses of the cart and block respectively
So, by using this concept -
Force acting on block $A$

$
W=f_L=m g=\mu(m b) \Rightarrow b=\frac{g}{\mu}
$

Hence, the answer is the option (3)

Summary

Skidding on a level road occurs when a vehicle loses traction, often due to sudden braking, sharp turns, or slippery conditions. The concept of pseudo-force helps explain this phenomenon, as it accounts for the forces acting on a block (or vehicle) when there is acceleration. By considering the minimum force and acceleration needed to prevent skidding, one can understand the relationship between friction, mass, and motion, helping to predict and prevent such incidents.