Surface Tension - Definition, Examples, Formula, Unit, Dimension, FAQs

Surface tension is the tendency of fluid surfaces to shrink into the minimum surface area possible. Have you noticed when you fill a glass up to the brim with water, you can still add a few more drops till it spills out? Or have you ever broken a thermometer and observed how the fallen mercury behaves? All these happen due to the surface tension of the surface. Let us understand the concept, surface tension definition along with its SI unit, formula and examples.

This concept is the part of properties of solids and liquids which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, VITEEE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of three questions have been asked on this concept. And for NEET one questions were asked from this concept.

Surface Tension

Surface tension is the elastic tendency of a fluid surface which makes it acquire the least surface area.

If we draw an imaginary line on the free surface of the liquid as shown in the below figure.

Then Surface tension of a liquid is measured by the force acting per unit length on either side of an imaginary line.

So Surface tension of a liquid is given by

$T=\frac{F}{l}$

Where:
F→ force
l→ imaginary length

The direction of this force is perpendicular to the line and tangential to the free surface of the liquid.

It depends only on the nature of the liquid and is independent of the area of the surface or length of the imaginary line considered.

• It is a scalar quantity.

Unit of Surface Tension

• Force is measured in newtons ( N ).
• Length is measured in meters (m).

$$
T=\frac{\mathrm{N}}{\mathrm{~m}}=\mathrm{N} / \mathrm{m}
$$
SI Unit: $\mathrm{N} / \mathrm{m}$.

• Dimensional Formula: $[T]=M T^{-2}$.

Example- Raindrops are spherical in shape because each drop tends to acquire minimum surface area due to surface tension, and for a given volume, the surface area of the sphere is minimum.

The surface tension of liquid decreases with the rise in temperature.

For More Information On Surface Tension, Watch The Below Video:

Solved Example Based On Surface Tension

Example 1: A drop of liquid of density ρ is floating half immersed in a liquid of density σ and surface tension 7.5×10−4Nem−1. The radius of drop-in will be :
(g=10 ms−2)

1) 15(2ρ−σ) 2) 15(ρ−σ) 3) 32(ρ−σ) 4) 320(2ρ−σ)

Solution:

B+T(2πR)=mgσ×2πR33 g+(2πR)=ϱ×2πR33 gσR2 g3+T=ϱR2 g37.5×10−2=R2 g3(ϱ−σ)R=32(ρ−σ)

Hence, the answer is option (3).

Example 2: A spherical soap bubble of radius 3 cm is formed inside another spherical soap bubble of radius 6 cm. If the internal pressure of the smaller bubble of radius 3 cm in the above system is equal to the internal pressure of another single soap bubble of radius r cm. The value of r is___________.

1) 2

2) 4

3) 3

4) 1

Solution:

Pi−P=4 Tr1P−Po=4 Tr2Pi−Po=4 Tr1+4 Tr2→(1)

Pi−Po=4 Tr→(2) From eq. (1) and (2) 4tr=4 Tr1+4 Tr2 (Given) 1r=1r1+1r2=13+16=918r=2 cm

Hence, the answer is option (1).

Example 3: A thin liquid film formed between a U- U-shaped wire and a light slider supports a weight of 1.5 10^-2 N ( see figure) The length of the slider is 30 cm and its weight is negligible. The surface tension of the liquid film is:

1) 0.0125 Nm^-1

2) 0.1 Nm^-1

3) 0.05 Nm^-1

4) 0.025 Nm^-1

Solution:

The force due to the surface tension will balance the weight.

2TL=wT=w2L

Substituting the given values, we get
T=1.5×10−2 N2×30×10−2 m=0.025Nm−1

Hence, the answer is option (4).

Example 4: On heating water, bubbles being formed at the bottom of the vessel detach and rise. Take the bubbles to be spheres of radius R and making a circular contact of radius r with the bottom of the vessel. If r << R, and the surface tension of water is T, value of r just before bubbles detach is :(density of water is )

1) R22pwg3T
2) R2pwg6T
3) R2pwgT
4) R23pwgT

Solution:

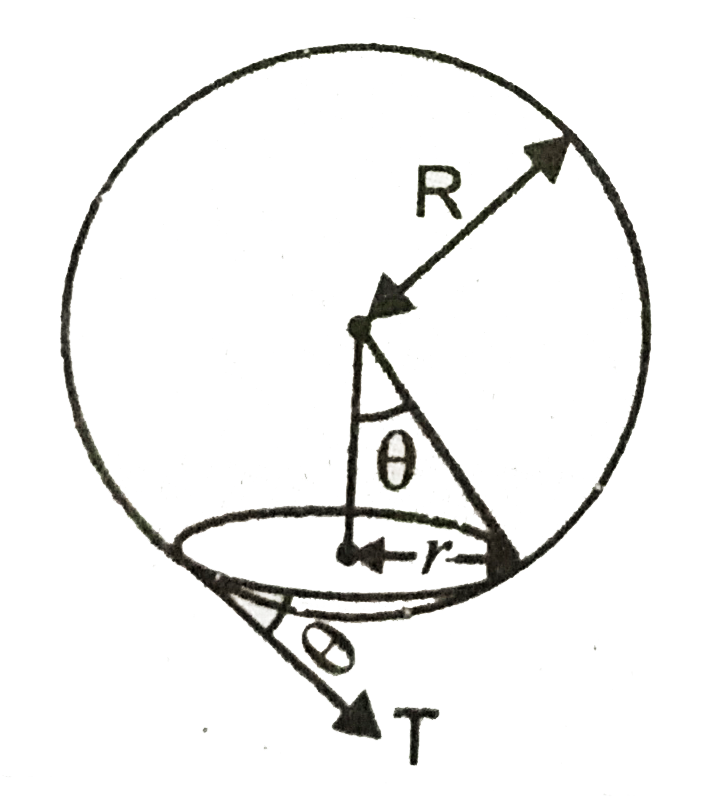
Here T is the surface tension and we know that surface tension,

T=Fl=F=Tl=T(2πr),

where F is the force due to surface tension and its vertical component will be T(2πr)Sinθ. .

Now The bubble will detach, if Buoyant force ≥ vertical component of surface tension force, so for the bubble to just detach:-

vertical component of surface tension force=buoyant force(or upthrust)

T(2πr)Sinθ=Vρwg⇒T(2πr)rR=43πR3ρwg⇒r2=2R4ρwg3T⇒r=R22ρwg3T

Hence, the answer is option (1).

Example 5: A soap bubble, blown by a mechanical pump at the mouth of a tube, increases in volume, with time, at a constant rate. The graph that correctly depicts the time dependence of pressure inside the bubble is given by :

1)

2)

3)

4) none of these

Solution:

Pressure Difference in Water Droplet -

$\Delta P=\frac{2 T}{R}$

wherein:

T- Surface tension

R- Radius

$V=c t^{4 / 3}=\frac{4}{3} \pi R^3$

$
R=K t^{1 / 3}
$
$
P=P_0+\frac{4 T}{K t^{1 / 3}}
$
$
P=P_0+C t^{-1 / 3}
$

Hence, the answer is option (4).