Thermal Expansion

Thermal expansion is a fundamental concept in physics that describes how the dimensions of a material change in response to temperature variations. When a substance is heated, its particles gain energy and move more vigorously, causing the material to expand. Conversely, cooling a substance results in contraction. This phenomenon plays a crucial role in various real-life applications, from the design of bridges and railways to everyday items like thermometers and metal lids on jars. Engineers must account for thermal expansion to prevent structural damage, while simple household tasks, such as loosening a tight metal lid by running it under hot water, also rely on this principle. Understanding thermal expansion helps us design safer, more efficient structures and solve practical problems in our daily lives.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Thermal Expansion
2. Effects of Thermal Expansion on Solids
3. Solved Examples Based on Thermal Expansion
4. Summary

Thermal Expansion

Thermal expansion is the tendency of a material to change its shape, area, and volume in response to a change in temperature. So, if there is any change in temperature every material has a tendency to change its dimension and the amount of change depends on the type of material.

Thermal expansion is minimum in the case of solids but maximum in the case of gases because the intermolecular force is maximum in solids but minimum in gases.

So, solids can expand in one dimension, two dimensions and three dimensions while liquids and gases usually suffer change in volume only.

Thermal expansion is basically of three types

Linear Expansion

When a solid is heated and its length increases, then the expansion is called linear expansion.

Let us take a specimen of length L₀. There are two scenarios, the first is before heating and the second image shows after heating. So,

(i) Change in the length of the specimen is $\Delta L=L_o \alpha \Delta T$ (Here, $L=$ Original length, $\Delta T=$ Temperature change)
(ii) The final length of the specimen is $L=L_o(1+\alpha \Delta T)$
(iii) Co-efficient of linear expansion $\alpha=\frac{\Delta L}{L_0 \Delta T}$
(iv) Unit of $\alpha$ is ${ }^{\circ} \mathrm{C}^{-1}$ or $K^{-1}$. It's dimension is $\left[\theta^{-1}\right]$

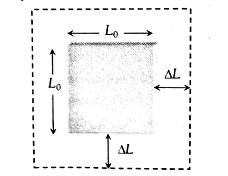
Superficial (Areal) Expansion:

When the temperature of a 2-dimensional specimen is changed, its area changes, then the expansion is called superficial or areal expansion.

(i) Change in area is $\Delta A=A_o \beta \Delta T$
( $A=$ Original area, $\Delta T=$ Temperature change)
(ii) Final area $A=A_o(1+\beta \Delta T)$
(iii) Co-efficient of superficial expansion $\beta=\frac{\Delta A}{A_0 \Delta T}$
(iv) Unit of $\beta$ is ${ }^{\circ} \mathrm{C}$ or $K$.

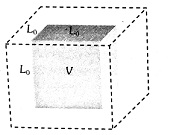
Volume or Cubical Expansion:

When a 3-dimensional solid is heated and its volume increases, then the expansion is called volume or cubical expansion.

Now there is one relation between the $\alpha, \beta$ and $\gamma$, which can be written as

$\alpha=\frac{\beta}{2}=\frac{\gamma}{3} \Rightarrow \alpha: \beta: \gamma=1: 2: 3$

Hence, for the same rise in temperature

Percentage change in area = 2 times the percentage change in length.
Percentage change in volume = 3 times the percentage change in length.

Effects of Thermal Expansion on Solids

Thermal stress in a rod which is rigidly fixed: When a rod is rigidly fixed at ends such as to prevent expansion or contraction when its temperature is increased or decreased. Due to preventing its thermal expansion or contraction, compressive or tensile stress is developed in it. As the rod tries to expand or contract, then it applies a reaction force on the rigid support. If the change in temperature of a rod of length L is $\Delta \theta$ then

Thermal strain $=\frac{\Delta L}{L}=\alpha \Delta \theta \quad\left[\right.$ As $\left.\alpha=\frac{\Delta L}{L} \times \frac{1}{\Delta \theta}\right]$

If we know the strain then with the help of Hooke's law, we can find the stress also. If we know the stress, then we can find the force by multiplying the cross-sectional area with stress. Both stress and force can be written as -

So, Thermal stress $=Y \alpha \Delta \theta$ or, Force on the supports $F=Y A \alpha \Delta \theta$

Recommended Topic Video

Solved Examples Based on Thermal Expansion

Example 1: Superficial expansion refers to

1) Expansion in area

2) Expansion in volume

3) Expansion in length

4) All of the above

Solution:

Superficial Expansion

When the temperature of a 2D object is changed its area changes. Called superficial expansion.

wherein

Hence, the answer is the option (1).

Example 2: The Coefficient of volume expansion of solid is x times the coefficient of superficial expansion then x is

1) 1.5

2) 2

3) 2.5

4) 3

Solution:

Relation between (alpha, beta & gamma)

$\begin{aligned} & \alpha=\frac{\beta}{2}=\frac{\gamma}{3} \\ & \alpha: \beta: \gamma \\ & 1: 2: 3 \\ & \gamma=\frac{3}{2} \beta=1.5 \beta \\ & x=1.5\end{aligned}$

Hence, the answer is the option (1).

Example 3: A solid metal ball has a spherical cavity. If the ball is heated the volume of the cavity will

1) Increase

2) Descrese

3) Remains unaffected

4) Remains unaffected but the shape of the cavity will change

Solution:

Volume/Cubical Expansion

When a solid is heated and its volume increases then the expansion is called volume or cubical expansion.

herein

Expansion of the cavity will take place.

Hence, the answer is the option (1).

Example 4: Each side of a box made of a metal sheet in cubic shape is 'a' at room temperature 'T', and the coefficient of linear expansion of the metal sheet is $' \alpha$ '. The metal sheet is heated uniformly, by a small temperature $\Delta T$, so that its new temperature is $T+\Delta T$. Calculate the increase in the volume of the metal box.

1) $4 \pi a^3 \alpha \Delta T$
2) $4 a^3 \alpha \Delta T$
3) $\frac{4}{3} \pi a^3 \alpha \Delta T$
4) $3 a^3 \alpha \Delta T$

Solution:

When a 3-dimensional solid is heated and its volume increases, then the expansion is called volume or cubical expansion.

Increase in the volume of metal box $=\Delta \mathrm{V}=\mathrm{V} \gamma \Delta \mathrm{T}$
Where V is the original volume

$
\begin{aligned}
& \because \gamma=3 \alpha \\
& \therefore \Delta \mathrm{V}=\mathrm{V}(3 \alpha) \Delta \mathrm{T} \\
& \Delta \mathrm{V}=3 \mathrm{a}^3 \alpha \Delta \mathrm{T}
\end{aligned}
$

Hence, the answer is the option (4).

Example 5: Uniform pressure P is exerted on all sides of a solid cube at temperature t°C. By what amount should the temperature be raised in order to bring the volume back to what it had been before the pressure was applied? (α= linear expansivity, ß= Bulk modulus)

1) $\frac{P \alpha}{\beta}$
2) $\frac{3 P \alpha}{\beta}$
3) $\frac{P}{\alpha \beta}$
4) $\frac{P}{3 \alpha \beta}$

Solution:

$\begin{array}{r}\left.\left(\frac{\Delta V}{V}\right)_1=r_{\Delta t}=3 \alpha(\Delta t)\left(\frac{\Delta V}{V}\right)_2=\frac{P V}{\beta}\right)_1=\left(\frac{\Delta V}{V}\right)_2 \text { or } 3 \alpha(\Delta t)=\frac{P}{\beta} \\ \therefore \Delta t=\frac{P}{3 \alpha \beta}\end{array}$

Hence, the answer is the option (4).

Summary

Thermal expansion occurs when a material rises in temperature and subsequently increases in size. The reason for this lies in the fact that the particles of the material move more and spread out when getting hotter. Thermal expansion can occur in any matter—solids, liquids, and gases—but is most observed in the solid state, such as metals. It is therefore a dilation that engineers and designers of bridges, buildings, and railways must account for, lest some support might give way and cause a catastrophe. For instance, rail gaps and expansion joints in bridges permit materials to expand safely and contract without dangerous stress. Designing for thermal expansion thus organs an element of safety into a wide variety of ordinary objects and large-scale architecture and infrastructure.