Thermo Couple

A thermocouple is a simple yet powerful device used to measure temperature, which works on the principle of the Seebeck effect. It consists of two different metal wires joined at one end, forming a junction that generates a voltage when exposed to a temperature difference. This voltage is then used to determine the temperature at the junction. Thermocouples are widely used in various industries, from monitoring the temperature in furnaces to ensuring the correct functioning of home appliances like ovens and water heaters. In our daily lives, thermocouples play a critical role in maintaining safety and efficiency, such as in the engines of cars, where they help regulate fuel combustion by measuring exhaust gas temperatures. Their ability to operate in extreme environments makes thermocouples indispensable in both industrial and household settings. In this article, we will discuss the concept of thermocouples, the Seeback Effect, neutral temperatures and solved examples for better understanding.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. What is a Thermocouple?
2. What is the Seeback Effect?
3. Neutral Temperature
4. Solved Examples Based on Thermo Couple
5. Summary

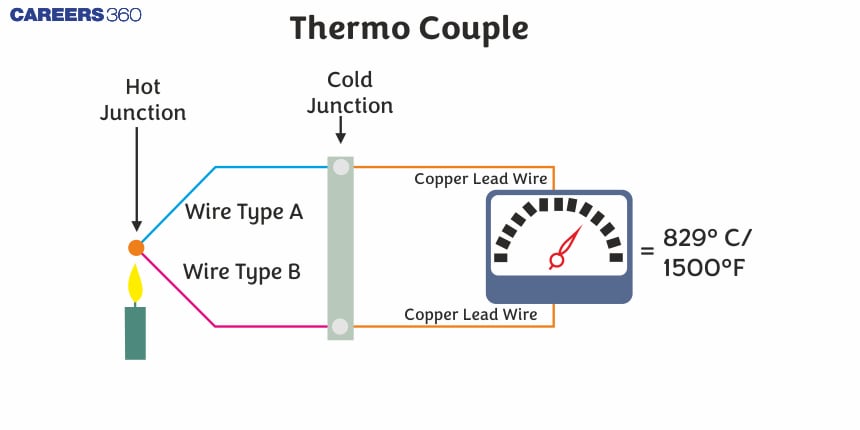
What is a Thermocouple?

Two wires of different metals are connected at two points to form two junctions. This thermoelectric device used to measure the temperature is called a thermocouple. If one junction of the thermocouple is at lower temperature and the other is at a higher temperature then a current starts flowing through the thermocouple.

What is the Seeback Effect?

According to this when the two junctions of a thermocouple are kept and maintained at different temperatures, then a current starts flowing through the loop made by conductors known as thermo-electric current. Because of this potential differences will develop between the junctions which are called thermoelectric emf which is of the order of a few micro-volts per degree temperature difference.

Seebeck arranged different metals in the decreasing order of their electron density. A few metals forming the series are as below.

Sb, Fe, Cd, Zn, Ag, Au, Cr, Sn, Pb, Hg, Mn, Cu, Pt, Co, Ni, Bi

Neutral Temperature

Neutral temperature, in the context of a thermocouple, refers to the specific temperature at which the net electromotive force (EMF) generated by the thermocouple is zero, despite the two junctions being at different temperatures. This occurs because the thermoelectric effects of the two different metals cancel each other out at this particular temperature.

Keeping the temperature of the cold junction constant and increasing the temperature of the hot junction, the emf increases and becomes maximum at a particular temperature. This temperature of the hot junction is called neutral temperature$\left(\theta_n\right)$. If the temperature is further increased the thermal emf starts decreasing and at a particular temperature, thermal emf becomes zero. If the temperature is further increased the thermal emf starts reversing. The temperature of the hot junction at which the thermal emf starts reversing is known as inversion temperature $\left(\theta_i\right)$

$\begin{aligned} & \theta_n=\frac{\theta_i+\theta_c}{2} \\ & \theta_n=\text { Neutral Temperature } \\ & \theta_i=\text { Inversion Temperature } \\ & \theta_c=\text { Cold Temperature }\end{aligned}$

Thermoelectric emf is given by the equation

$E=\alpha t+\frac{1}{2} \beta t^2$

where $\alpha$ and $\beta$ are thermo electric constant ( t = temperature of the hot junction).

For E to be maximum at t=t_n, we will differentiate the Electric field with respect to the temperature of the hot junction and we get

$\frac{d E}{d t}=0$ i.e. $\alpha+\beta t_n=0 \Rightarrow t_n=-\frac{\alpha}{\beta}$

If the temperature of the hot junction increases beyond the neutral temperature, then there is a decrease in the thermo emf and at a particular temperature it becomes zero, if heat is supplied further, the direction of emf is reversed. This temperature of the hot junction is called the temperature of inversion (t_i).

$t_n=\frac{t_i+t_c}{2}$

Here, t_c is the temperature of the cold junction.

We can understand better through video.

Solved Examples Based on Thermo Couple

Example 1: The thermo emf of a thermocouple varies with the temperature $\theta$ of the hot junction as $E=a \theta+b \theta^2$ in volt where the ratio a/b is 700°C. If the cold junction is kept at 0°C, then the neutral temperature is

1) 700°C

2) 350°C

3) 1400°C

4) no neutral temperature is possible for this thermocouple.

Solution:

Thermocouple

Current flow across the cold function from the later occurring metal in the series to the one occurring earlier in the thermoelectric series and reverse at the not junction.

$
\begin{aligned}
E & =a \Theta+b \Theta^2 \\
\frac{d E}{d \Theta} & =a+2 b \Theta \quad\left(\frac{a}{b}=700^{\circ} c\right)
\end{aligned}
$

At neutral temperature
$
\begin{aligned}
& \frac{d E}{d \Theta}=0 \\
& 0=a+2 b \Theta_n \\
& \Rightarrow \Theta_n=\frac{-a}{2 b} \\
& \Theta_n=\frac{-1}{2} \times(700) \\
& =-350^{\circ} \mathrm{c}
\end{aligned}
$

Neutral temperature is calculated to be $-350^{\circ} \mathrm{C}$ i.e. no neutral temperature is possible in this thermocouple.

Hence, the answer is the option (4).

Example 2: For a thermocouple, the neutral temperature is 270^o C and the temperature of its cold junction is 20^o C. If there is no deflection in the galvanometer, the temperature (in ) of the hot junction should be

1) 520

2) 540

3) 210

4) 209

Solution:

If the temperature of the hot junction increases beyond the neutral temperature, then there is a decrease in the thermo emf, and at a particular temperature it becomes zero, if heat is supplied further, the direction of emf is reversed. This temperature of the hot junction is called the temperature of inversion (t_i).

$
t_n=\frac{t_i+t_c}{2}
$

When there is no deflection, then this temperature is called inversion temperature. It is given by the relation $\theta_n=\frac{\theta_i+\theta_c}{2}$ Where $\theta_c$ is temperature of cold junction $=20^{\circ} \mathrm{C}$ and neutral

Here, t_c is the temperature of the cold junction.

temperature $\theta_n=270^{\circ} \mathrm{C} \therefore \theta_i=2 \theta_n-\theta_c=540-20=520^{\circ} \mathrm{C}$

Hence, the answer is the option (1).

Example 3: If $\theta_i$ is the inversion temperature, $\theta_n$ is the neutral temperature, $\theta_c$ is the temperature of the cold junction, then

1) $\theta_i+\theta_c=\theta_n$
2) $\theta_i-\theta_c=2 \theta_n$
3) $\frac{\theta_i+\theta_c}{2}=\theta_n$
4) $\theta_c-\theta_i=2 \theta_n$

Solution:

$\begin{aligned} & \theta_c+\theta_i=2 \theta_n \\ & \Rightarrow \theta_n=\frac{\theta_c+\theta_i}{2}\end{aligned}$

Hence, the answer is the option (3).

Example 4:A thermocouple is made from two metals, antimony and bismuth. If one junction of the couple is kept hot and the other is kept cold then, an electric current will

1) flow from antimony to bismuth at the cold junction

2) flow from antimony to bismuth at the hot junction

3) flow from bismuth to antimony at the cold junction

4) not flow through the thermocouple.

Solution:

At cold junction, current flows from Antimony to Bismuth (because current flows from metal occurring later in the series to metal occurring earlier in the thermoelectric series).

Hence, the answer is the option (1).

Summary

Thermocouples are essential devices for measuring temperature, operating on the Seebeck effect, where different metal junctions generate an electromotive force (EMF) when exposed to temperature differences. Key concepts include the neutral temperature, where EMF is zero, and the inversion temperature, where EMF reverses direction. Understanding these principles is crucial for accurate temperature measurement in various applications, from industrial processes to everyday appliances.