To Determine Resistance Of A Galvanometer By Half-deflection Method And To Find Its Figure Of Merit

Determining the resistance of a galvanometer using the half-deflection method is an essential experiment in understanding the fundamentals of electrical measurements. The half-deflection method involves adjusting the known resistance in the circuit until the galvanometer needle deflects to half its initial full-scale value. This method provides an accurate measurement of the internal resistance of the galvanometer and helps in calculating its figure of merit, which indicates the sensitivity of the device. In real life, this experiment is crucial for designing and calibrating precise measuring instruments used in various fields such as electrical engineering, medical diagnostics (like ECG machines), and scientific research.

This Story also Contains

1. Aim To determine the resistance of a galvanometer by the half-deflection method and to find its figure of merit.
2. Apparatus Required
3. Theory
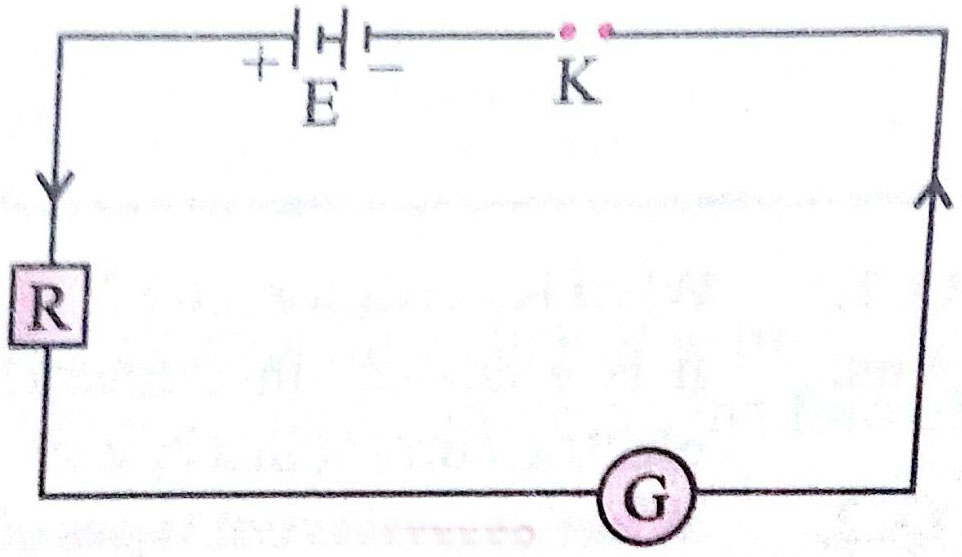
4. Circuit Diagram
5. Procedure
6. Calculations
7. Viva Voce Questions and Answers
8. Solved Examples Based on Determining the Resistance of A Galvanometer By the Half-deflection Method And Find Its Figure Of Merit
9. Summary

Aim
To determine the resistance of a galvanometer by the half-deflection method and to find its figure of merit.

Apparatus Required

• A Weston-type galvanometer
• A voltmeter,
• A battery or battery eliminator
• Two resistance boxes $(10,000 \Omega$, and $200 \Omega)$
• Two one-way keys, a rheostat, and a screw gauge.
• A meter scale
• An ammeter of the given range
• Connecting wires and a piece of sandpaper.

Theory

(i) The resistance of the given galvanometer as found by the half-deflection method
$
G=\frac{R \cdot S}{R-S} \ldots \ldots (1)
$

where R is the resistance connected in series with the galvanometer and S is the shunt resistance.

(ii) The figure of merit

$k=\frac{E}{(R+G) \theta} \ldots$ (2)

where E is the e.m.f. of the cell and $\theta$ is the deflection produced with resistance R

(iii) The maximum current that can pass through the galvanometer,
$
i_g=n k \ldots
$
where n is the total number of divisions on the galvanometer scale on either side of zero.

Circuit Diagram

Procedure

(a) The resistance of a galvanometer by half deflection method

1. Make the connections accordingly as shown in the circuit diagram.

2. See that all plugs of the resistance boxes are tight.

3. Take out the high resistance (say $2000 \Omega$ ) from the resistance box R and insert the key K₁ only.

4. Adjust the value of R so that deflection is maximum, even in number and within the scale.

5. Note the deflection. Let it be $\theta$.

6. Insert the key also and without changing the value of R, adjust the value of S, such that deflection in the galvanometer reduces to exactly half the value obtained in step 5 i.e.$\frac{\theta}{2}

7. Note the value of resistance S

8. Repeat steps 4 to 7 three times taking out different values of R and adjusting S every time.

(b) Figure of Merit

9. Take one cell of the battery (battery eliminator) and find its E.M.F. by a voltmeter by connecting + ve of the voltmeter with +ve of the cell and-ve of the voltmeter with-ve of the cell. Let it be E.
10. Make connections as in the circuit diagram.

11. Adjust the value of R to obtain a certain deflection of 0 (say 30 divisions) when the circuit is closed.
12. Note the values of resistance R and deflection $\theta$.
13. Now change the value of R and note the galvanometer deflection again.

14. Repeat steps 9 to 13 with both cells of the battery with different voltages like 2,4,6,8 volts from the battery eliminator.
15. Find the figure of merit k using the formula.

Calculations

Calculation for G

1. Calculate G using

$G=\frac{R \cdot S}{R-S}$

2. Calculate the mean value of G

Calculation for k

1. Calculate k using

$k=\frac{E}{(R+G) \theta}$

2. Calculate the mean value of k

Result
1. The resistance of the given galvanometer $=\ldots \Omega$
2. The figure of merit of the given galvanometer = ..... Ampere per division.

Viva Voce Questions and Answers

Question: What is a Galvanometer?

Answer: A galvanometer is a device used to detect small electric currents in a circuit. It operates on the principle of the torque experienced by a current-carrying coil in a magnetic field.

Question: Define the Figure of Merit of a Galvanometer.

Answer: The figure of merit of a galvanometer (denoted by K) is the current required to produce a deflection of one scale division in the galvanometer. It is expressed in ampere per division (A/division) and is given by the formula:

$K=\frac{I}{\theta}$

Question: Why is the method called the Half Deflection Method?

Answer: The method is called the half deflection method because it involves adjusting a shunt resistance SSS such that the deflection in the galvanometer is reduced to half of its initial value. This ensures that the current divides equally between the shunt and the galvanometer, allowing for precise calculations of the internal resistance and current sensitivity.

Solved Examples Based on Determining the Resistance of A Galvanometer By the Half-deflection Method And Find Its Figure Of Merit

Example 1: To find the resistance of a galvanometer by the half deflection method the following circuit is used with resistances $R_1=9970 \Omega, R_2=30 \Omega$ and $R_3=0 \Omega$. The deflection in the galvanometer is d. With $R_3=107 \Omega$ the deflection changed to $\frac{d}{2}$. The galvanometer resistance is approximately

1) $107 \Omega$
2) $137 \Omega$
3) $\frac{107}{2} \Omega$
4) $77 \Omega$

Solution:

At initial condition, $\mathrm{R}_3=0$
Equivalent resistance of $R_2 \& R_3=30 \Omega$

When $R_3=107 \Omega \& R_2=30 \Omega$, then equivalent resistance should be $30 / 2$

$
=15 \Omega
$

this will be when equivalent resistance $R(\mathrm{~g}), R 3$ will be parallel to $R 2$, we get resistance of $15 \Omega$

$
\begin{aligned}
& \text { Let } R g-R 3=R(e q) \\
& 1 / R 2+1 / R(e q)=1 / 30+1 / 30=1 / 15 \\
& R(e q)=30 \Omega \\
& \therefore R 3-R g=30 \\
& \therefore 107-R g=30 \\
& \therefore R g=77 \Omega
\end{aligned}
$

Hence, the answer is the option (1).

Example 2: What is meant by the figure of merit of a galvanometer?

1) Current required to produce unit deflection on the galvanometer

2) Maximum deflection on the galvanometer

3) Voltage required to produce unit deflection on the galvanometer

4) None of these

Solution:

To find the figure of merit of a galvanometer

$
K=\frac{1}{\theta}\left(\frac{E}{R+G}\right)
$

wherein
$K=$ Figure of merit
$\theta=$ deflection angle
$\mathrm{E}=$ battery
$\mathrm{R}=$ Resistance
$\mathrm{G}=$ Galvanometer Resistance

The figure merit of the galvanometer is currently required to produce unit deflection on the galvanometer.

Hence, the answer is the option (1).

Example 3: In a circuit designed to find the resistance of a galvanometer using the half-deflection method, a 6 V battery and a high resistance of $11 \mathrm{k} \Omega$ are connected. The figure of merit of the galvanometer is $60 \mu \mathrm{~A} /$ division. When no shunt resistance is connected, the galvanometer shows a deflection of $\theta=9$ divisions due to the current in the circuit. Determine the value of the shunt resistance (in $\Omega$ ) required to reduce the deflection to $\theta / 2$.

1) 110

2) 220

3) 55

4) 0

Solution:
$
\begin{aligned}
& I=9 \times 60 \mu A \\
& \frac{6}{11000+G}=540 \times 10^{-6} \\
& G=\frac{1000}{9} \\
& G=\frac{R S}{R-S} \\
& \frac{1000}{9}=\frac{11000 S}{11000-S}
\end{aligned}
$
This gives $\mathrm{S}=110 \Omega$

Hence, the answer is the option (1).

Example 4: You are given a galvanometer with a full-scale deflection of 40 divisions for a current of 1.5 mA. The shunt resistor used in conjunction with the galvanometer has a known resistance of 8.0 Ω. Using the half-deflection method, determine the resistance and figure of merit (sensitivity) of the galvanometer.

1) 0.007 A/Div

2) 170 A/Div

3) 200 A/Div

4) 20 A/Div

Solution:

Given data:
$
\begin{aligned}
& \mathrm{I}_{\mathrm{fsd}}=1.5 \mathrm{~mA} \\
& \mathrm{~N}=40 \text { divisions } \\
& \mathrm{R}_{\mathrm{sh}}=8.0 \Omega
\end{aligned}
$
Step 1: Calculate the half-scale deflection current ( $\left.1_{\text {hsd }}\right)$ :
Using the relation between currents and deflections:

$
\frac{I_{\mathrm{fsd}}}{N}=\frac{I_{\mathrm{hsd}}}{\frac{N}{2}}
$
Substituting the given values:

$
\frac{1.5 \mathrm{~mA}}{40}=\frac{I_{h s d}}{20}
$
Solving for Ihsd:

$
I_{h s d}=\frac{1.5 m A}{40} \times 20=0.75 m A
$

Step 2: Calculate the resistance (R) of the galvanometer: Using Ohm’s law:
$
R=\frac{V}{I_{h s d}}
$
The total current passing through the circuit is the sum of the galvanometer current and the shunt current:

$
I_{\text {total }}=I_{\text {galvanometer }}+I_{\text {shunt }}
$
Since the shunt resistor is chosen such that most of the current flows through it, Itotal can be approximated as $\mathrm{I}_{\text {shunt: }}$

$
I_{\text {total }} \approx I_{\text {shunt }}=\frac{I_{f s d} \times R_{\text {sh }}}{R_{s h}+R}
$
Solving for R:

$
R=\frac{I_{f s d} \times R_{s h}}{I_{\text {total }}-I_{\text {Shunt }}}
$
Substituting the values:

$
R=\frac{(1.5 \mathrm{~mA}) \times(8.0 \Omega)}{0.0015 \mathrm{~A}-\frac{1.5 \mathrm{~mA} \times 8.0 \Omega}{R}}
$
Solving this quadratic equation for $R$ gives two possible solutions. We choose the physically meaningful one:

$
R \approx 12.42 \Omega
$
Step 3: Calculate the figure of merit (M):

The figure of merit (sensitivity) is given by the formula:
$
M=\frac{I_{\mathrm{hsd}} \times R}{I_{\text {fdd }} \times N}
$
Substituting the values:

$
M=\frac{(0.75 \mathrm{~mA}) \times(12.42 \Omega)}{(1.5 \mathrm{~mA}) \times 40}
$
Simplifying:

$
M \approx 0.007 \mathrm{~A} / \mathrm{Div}
$

The resistance of the galvanometer is approximately 12.42 Ω, and the figure of merit (sensitivity) is approximately 0.007 A/Div.

Hence, the answer is the option (1).

Example 5: You are conducting an experiment where you need to measure very small currents accurately. You have a galvanometer with a full-scale deflection of 50 divisions for a current of 1.0 mA. The internal resistance of the galvanometer is 20 Ω. To achieve higher sensitivity, you decide to use a shunt resistor. Determine the shunt resistance required to achieve a half-scale deflection for a current of 0.2 mA.

1) 160Ω

2) 170Ω

3) 200Ω

4) 20Ω

Solution:

Given data:
$
\begin{aligned}
& \mathrm{I}_{\text {fsd }}=1.0 \mathrm{~mA} \\
& \mathrm{~N}=50 \text { divisions } \\
& \underline{I}_{\text {hsd }}=0.2 \mathrm{~mA} \\
& R_{\text {internal }}=20 \Omega
\end{aligned}
$
Step 1: Calculate the shunt current (Ishunt):
Using the relation between currents and deflections:

$
\begin{aligned}
& \frac{I_{\mathrm{fsd}}}{N}=\frac{I_{\mathrm{hsd}}}{\frac{N}{2}} \\
& \text { Solving for } I_{\text {shunt }}= \\
& I \text { shunt }=\left(\frac{1.0 \mathrm{~mA}}{50}\right) \times \frac{50}{2}=0.5 \mathrm{~mA}
\end{aligned}
$

Step 2: Calculate the total current through the shunt resistor (I_total):

The total current passing through the circuit is the sum of the galvanometer current and the shunt current:
$
I_{\text {total }}=I_{\text {galvanometer }}+I_{\text {shunt }}
$
Solving for $\mathrm{I}_{\text {galvanometer: }}$

$
I_{\text {galvanometer }}=I_{\text {total }}-I_{\text {shunt }}
$
Substituting the given values:

$
\mathrm{I}_{\text {galvanometer }}=1.0 \mathrm{~mA}-0.5 \mathrm{~mA}=0.5 \mathrm{~mA}
$

Step 3: Calculate the voltage drop across the shunt resistor (V_shunt):

Using Ohm’s law:

$\begin{aligned} & V_{\text {shunt }}=I_{\text {shunt }} \times R_{\text {shunt }} \\ & \text { Solving for } \mathrm{R}_{\text {shunt: }} \\ & R_{\text {shunt }}=\frac{V_{\text {shunt }}}{I_{\text {shunt }}} \\ & \text { Substituting } V_{\text {shunt }}=I_{\text {total }} \times R_{\text {internal }}: \\ & \qquad R_{\text {shunt }}=\frac{I_{\text {total }} \times R_{\text {internal }}}{I_{\text {shunt }}} \\ & \text { Substitutingthevalues : } R_{\text {shunt }}=\frac{0.5 \mathrm{~mA} \times 20 \Omega}{0.5 \mathrm{~mA}}=20 \Omega\end{aligned}$

To achieve a half-scale deflection for a current of 0.2 mA, a shunt resistor with a resistance of 20 Ω is required.

Hence, the answer is the option (4).

Summary

In order to find out how much resistance a galvanometer has, one should make use of the half-deflection approach. A known high resistor is then connected in series with the galvanometer and also with a source of voltage. A deviation must be created on this circuit so as to cause deflection of the galvanometer. Then, adding shunt resistance will bring about a change in it such that half of its initial value occurs this time around; hence you can calculate the galvanometer’s own resistance values. On the other hand, the current flowing through the measuring instrument here is what gives meaning to the figure of merit, which indicates the amount needed for one full-scale deflection.