To Find The Mass Of A Given Body Using A Metre Scale By Principle Of Moments

For a system in equilibrium, the principle demands that the total moments in a clockwise direction should equal those in counter-clockwise directions. If you balance such a scale on its pivot using a meter stick as if it were a force multiplier or lever arm you can unravel the mass of an unknown object. By placing an object whose mass is unknown on one side of the meter stick and balancing it by adding a known mass on the other side, we can work out what is the unknown mass.

The principle of moments is very important. It shows us how we can get the weight of any object using a meter rule. If we make the moment of force about the pivot point equal on both sides, we will weigh our object accurately by taking advantage of the state of balance. This is very important especially when it comes to applying physics in real-life situations since it guarantees that experimental arrangements are accurate. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of one question has been asked on this concept.

Aim

To determine the mass of a given body using a metre scale by the principle of moments.

Apparatus

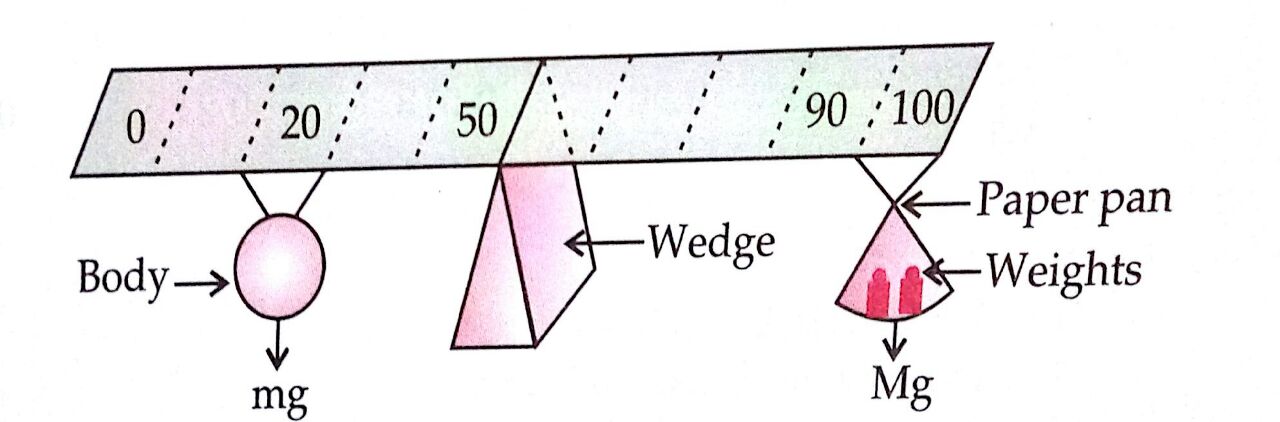
A metre scale, a broad heavy wedge with a sharp edge, a weight box, a body of unknown mass.

Theory

If m and M are the mass of the body and the mass of the weight used and a and A are the distances of their loops from wedge. Then, power (mass) arm =a, weight arm =A
From the principle of moments m.g.a=M.g.A

$m=M \frac{A}{a}$

m = mass of body

M is the mass of the weight

A is the distance from the wedge

Calculation

Mean mass, $\quad m=\frac{m_1+m_2+m_3}{3} \mathrm{~g}=\ldots \mathrm{g}$
It will be found that $\quad M_1=M_2=M_3=m$ in all cases.

Procedure

1. Arrange the meter scale in a horizontal position by supporting it at the 50 cm mark at the sharp edge of the broad heavy wedge.

2. Take a loop thread.

3. Suspended the given body whose mass is to be determined by the loop thread at a fixed mark on the left of the wedge.

4. Suspend a paper pan on the right side of the wedge.

5. Put some known weight in the pan.

Result
The unknown mass of the body, $\mathrm{m}=\ldots \mathrm{g}$.

Precautions

1. The wedge should be broad and heavy with a sharp edge.
2. The metre scale should have uniform mass distribution.
3. Threads used for loops should be thin, light and strong

Solved Examples Based on Find The Mass of a Given Body Using a Metre Scale by Principle of Moments

Example 1: The wedge is kept below the 60 cm mark on the meter scale known masses of 1 kg and 2 kg is hung at the 20 cm and 30 cm mark respectively. Where will a 4 kg mass be hung on the meter scale to balance it? (in cm)

1) 85

2) 90

3) 70

4) 75

Solution:

To find the mass of a given body using a metre scale by the principle of moments

As we learn

To find the mass of a given body using a metre scale by the principle of moments

$m=M \frac{A}{a}$

Calculation

$m=\frac{m_1+m_2+m_3}{3}$

m = mean mass

At equilibrium, net moment = 0

$\begin{aligned} & \Rightarrow 1 \mathrm{~kg} \times 40 \mathrm{~cm}+2 \mathrm{~kg} \times 30 \mathrm{~cm}=4 \mathrm{~kg} x \\ & x=25 \mathrm{~cm} \text { (from wedge) }\end{aligned}$

Distance from end = 85 cm

Hence, the answer is the option (1).

Example 2: A metre scale is balanced on a knife edge at its centre. When two coins, each of mass 10 g are put on top of the other at the 10.0 cm mark the scale is found to be balanced at the 40.0 cm mark. The mass of the metre scale is found to be $\mathrm{x} \times 10^{-2} \mathrm{~kg}$. The value of x is $\qquad$ .

1) 6

2) 8

3) 7

4) 5

Solution:

Let the mass of the metre scale \&
Coin be $M$ and $m$ respectively.
For a scale to be balanced, $\Sigma \mathrm{F}=0$ and $\Sigma \tau=0$
$R$ is the reaction force on a knife edge

$
\begin{aligned}
& \Sigma \mathrm{F}=0 \\
& \mathrm{R}=2 \mathrm{mg}+\mathrm{Mg} \\
& \Sigma \tau=0
\end{aligned}
$

about knife edge

$
\begin{aligned}
& (2 \mathrm{mg})(30)(\leftarrow)+\mathrm{Mg} \times 10(\rightarrow)=0 \\
& \mathrm{~m}=\frac{\mathrm{M}}{6} \Rightarrow \mathrm{M}=6 \mathrm{M} \\
& \quad=609 \\
& \mathrm{M}=6 \times 10^{-2} \mathrm{~kg} \\
& \therefore \mathrm{x}=6
\end{aligned}
$

Hence, the answer is the option (1).

Example 3: A meter scale with a least count of 0.1 cm is used to measure the length of an object. The zero of the scale coincides with one end of the object. The measured length is found to be 37.8 cm. Determine the actual length of the object, considering the zero error.

1) 40 cm

2) 37.8 cm

3) 45 cm

4) 37.8 mm

Solution:

Given:

Least count of meter scale L = 0.1 cm

The measured length of the object L_measured = 37.8 cm

Step 1: Determine the zero error (E_zero) of the meter scale. Since the zero of the scale coincides with one end of the object, E_zero = 0 cm.

Step 2: Calculate the actual length (L_actual) of the object using the corrected length:

L_actual = L_measured - E_zero

L_actual = 37.8 cm - 0 cm

Step 3: Calculate L_actual:

L_actual = 37.8 cm

The actual length of the object is 37.8 cm.

Hence, the answer is the option (2).

Example 4: An experiment is conducted to measure the length of a metal rod using a meter scale. The reading on the meter scale at the left end is 5 cm, and the reading at the right end is 21 cm. Determine the length of the metal rod.

1) 16 mm

2) 160 cm

3) 160 mm

4) 1.6 cm

Solution:

Given values:

Reading at the left end (L) = 5 cm

Reading at the right end (R) = 21 cm

The length of the metal rod (D) can be calculated by subtracting the reading at the left end from the reading at the right end:

D = R - L

Calculate the length of the metal rod:

D = 21 cm - 5 cm = 16 cm

The length of the metal rod is 16 cm.

The length of the metal rod is calculated to be 16 cm or 160 mm.

Hence, the answer is the option (3).

Example 5: A torque metre is calibrated to reference standards with the mass, length and also with time, each will have 15% accuracy, after this calibration, measured torque with this torque meter, we will have net accuracy is

1) 78%

2) 76%

3) 75%

4) 80%

Solution:

As torque

$\begin{aligned} & =m L^2 T-2 \\ \frac{\Delta \tau}{\tau} & =\frac{\Delta m}{m}+\frac{2 \Delta L}{L}+2 \frac{\Delta T}{T}\end{aligned}$

$\begin{array}{r}\frac{\Delta \tau}{\tau} \times 100=15+2 \times 15+2 \times 15 \\ =15+30+30 \\ =75 \%\end{array}$

Hence, the answer is the option (3).

Summary

In order to determine the magnitude of a body located at an unknown distance, one uses a meter rule in conformity with the moment's principle. Here, one end is brought into equilibrium with the body, while another known quantity constitutes the other in terms of weight distribution or placement. If we were to consider balance, it would mean that when the object from one direction exerts a force (or pulls), there is another force acting upon it from the other direction to keep everything stable and ensure no topple-over.