Torque On An Electric Dipole In A Uniform Electric Field

Introduction

An electric dipole consists of two equal and opposite charges separated by a small distance. When placed in a uniform electric field, the dipole experiences a force on each charge, but since the forces are equal and opposite, they create a torque instead of causing linear motion. This torque tends to align the dipole with the direction of the electric field. The strength of the torque depends on the magnitude of the dipole moment, the strength of the electric field, and the angle between the dipole moment and the field. This concept helps explain how molecules behave in electric fields and is fundamental in understanding polarization effects.

Net Force

When a dipole is kept in a uniform electric field. The net force experienced by the dipole is zero as shown in the below figure.

$
\text { l.e } F_{n e t}=0
$

Hence dipole will not make any linear motion.

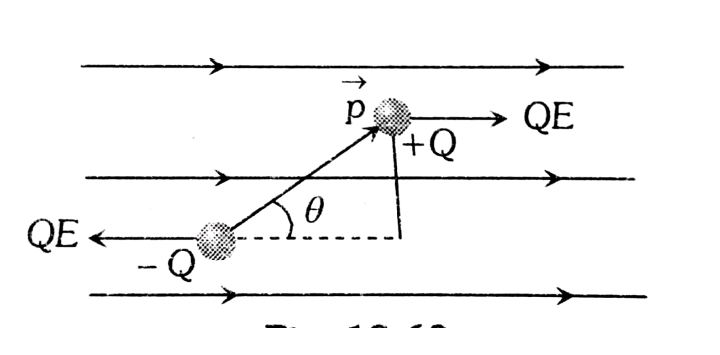
Torque on dipole

Net torque about the centre of the dipole is given as $\tau=Q E d \sin \theta$
Using $P=Q d_{\text {we get }} \tau=P E \sin \theta$
So $\vec{\tau}=\vec{P} \times \vec{E}$
- The direction of the torque is normal to the plane containing dipole moment $P$ and electric field $E$ and is governed by the right-hand screw rule.
- If Dipole is parallel to E the torque is Zero. I.e $\Theta=0^{\circ} \quad \tau=0$ (This is the position of stable equilibrium of dipole)

• - Torque is maximum when Dipole is perpendicular to E. I.e $\Theta=\frac{\pi}{2} \quad \tau=P E=$ maximum torque

Oscillation of dipole -If a dipole experiencing a torque in an electric field is allowed to rotate, then it will rotate to align itself to the Electric field. But when it reaches along the direction of E the torque becomes zero. But due to inertia, it overshoots this equilibrium condition and then starts oscillating about this mean position.

The time period of this oscillation is given as

$T=2 \pi \sqrt{\frac{I}{P E}}$

where I= moment of inertia of dipole about the axis passing through its centre and perpendicular to its length.

Dipole in Non-Uniform Electric Field- In case the Electric field is non-uniform, the magnitude of the force on +q and –q will be different. So $F_{(}$net $) \neq 0$ and At the same time due to a couple of forces acting, a torque will also be acting on it.

Recommended Topic Video

Some Solved Examples

Example 1:An electric dipole is placed at an angle of 30^o to a non- ­uniform electric field. The dipole will experience

1)a torque only

2)a translational force only in the direction of the field

3)a translational force only in a direction normal to the direction of the field

4) a torque as well as a translational force.

Solution:

Torque Experienced by the dipole -

$
\begin{aligned}
& \vec{\tau}=\vec{p} \times \vec{E} \\
& \tau=p E \sin \Theta
\end{aligned}
$
The force experienced by dipole placed in a non-uniform Electric field
The potential energy of the dipole placed in the Electric field

$
U=-p E \cos \theta \therefore F=-\frac{d U}{d x}=-p \cos \theta \frac{d E}{d x}
$
In a non-uniform electric field, the dipole will experience a torque as well as a translational force.
Example 2: The torque acting on a dipole of the moment $\vec{p}$ in an electric field $\vec{E}$ is
1) $\vec{p} \cdot \vec{E}$
2) $\vec{p} \times \vec{E}$
3)zero
4) $\vec{E} \times \vec{p}$

Solution:

As we have learned

Torque Experienced by the dipole -

$
\begin{aligned}
& \vec{\tau}=\vec{P} \times \vec{E} \\
& \vec{\tau}=P E \sin \Theta \\
& \Theta=0^{\circ} \quad \tau=0
\end{aligned}
$
$
\Theta=\frac{\pi}{2} \quad \tau=\text { max }^m
$

- wherein

torque is vector product of dipole moment and electric field

Example 3: An electric dipole when placed in a uniform electric field $E$ will have minimum potential energy, if the positive direction of dipole moment makes the following angle with $E$
1) $\pi$
2) $\pi / 2$
3) zero
4)$^{3 \pi / 2} $
Solution:
Work done in rotation

$
W=P E\left(\cos \Theta_1-\cos \Theta_2\right)
$

- wherein

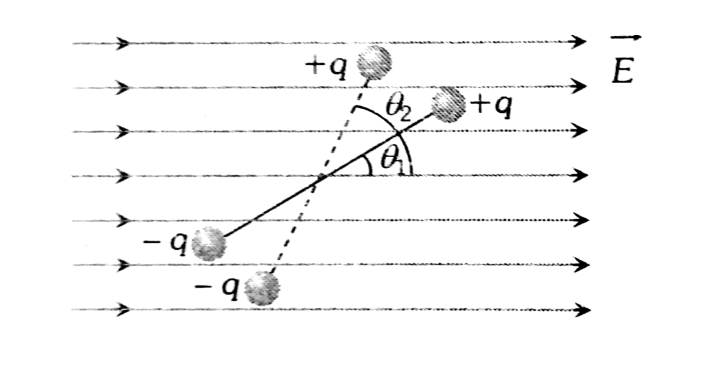
Potential energy = – pE cosϴ

When $\theta$ = 0. Potential energy = – pE (minimum)

Example 4 Two identical electric point dipoles have dipole moments $\overrightarrow{p_1}=p \hat{i}$ and $\overrightarrow{p_2}=-p \hat{i}$ and are held on the x axis at a distance 'a' from each other. When released, they move along the x -axis with the direction of their dipole moments remaining uchanged. If the mass of each dipole is ' $m$ ', their speed when they are infinitely far apart is :
$
\frac{P}{\text { 1) }} \sqrt{\frac{1}{\pi \epsilon_0 m a}}
$

2) $\frac{P}{a} \sqrt{\frac{1}{2 \pi \epsilon_0 m a}}$

$
\begin{aligned}
& \frac{P}{a} \sqrt{\frac{2}{\pi \epsilon_0 m a}} \\
& \frac{P}{a} \sqrt{\frac{3}{2 \pi \epsilon_0 m a}}
\end{aligned}
$

Solution:
Using energy conservation:

$
K E_i+P E_i=K E_f+P E_f
$
虫

$
\begin{aligned}
& \mathrm{O}+\frac{2 \mathrm{KP}^3}{\mathrm{a}^3} \times \mathrm{P}=\frac{1}{2} \mathrm{mv}^2 \times 2+0 \\
& \mathrm{~V}=\sqrt{\frac{2 \mathrm{P}^2}{4 \pi \mathrm{P}^3 \mathrm{~m}}}=\frac{\mathrm{P}}{\mathrm{a}} \sqrt{\frac{1}{2 \pi \varepsilon_{0 \mathrm{am}}}}
\end{aligned}
$

Summary

When an electric dipole is placed in a uniform electric field, it experiences a torque that tends to align it with the field direction. This torque results from the forces acting on the positive and negative charges in the dipole, which create a rotational effect rather than a net force. The strength of the torque depends on the dipole's moment, the electric field strength, and the angle between the dipole and the field. As the dipole rotates, the torque decreases, becoming zero when the dipole aligns with the electric field. This concept is important in understanding how molecules and other dipoles behave when exposed to external electric fields.