Types Of Semiconductor: Intrinsic And Extrinsic Semiconductor

Imagine the electronic devices you use every day—your smartphone, laptop, or even the LED lights in your home. All these devices rely on a special class of materials called semiconductors to function. Semiconductors are essential because they have properties that fall between those of conductors (like copper) and insulators (like glass). This unique property allows them to control electrical currents, making them the backbone of modern electronics.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. What is Intrinsic Semiconductor?
2. What is Extrinsic Semiconductor?
3. Solved Examples Based on Types Of Semiconductor: Intrinsic And Extrinsic Semiconductor
4. Summary

Now, let's dive into the two main types of semiconductors: intrinsic and extrinsic semiconductors. Understanding these types will give you insight into how semiconductors are engineered to meet the diverse needs of our electronic world.

What is Intrinsic Semiconductor?

It is a pure semiconductor. Silicon and germanium are the most common examples of intrinsic semiconductors. Both these semiconductors are most frequently used in the manufacturing of transistors, diodes and other electronic components.

Both Si and Ge have four valence electrons. In its crystalline structure, every Si or Ge atom tends to share one of its four valence electrons with each of its four nearest neighbour atoms, and also to take a share of one electron from each such neighbour as shown in the below figure. This shared pair of the electrons is called a Covalent bond or a Valence bond.

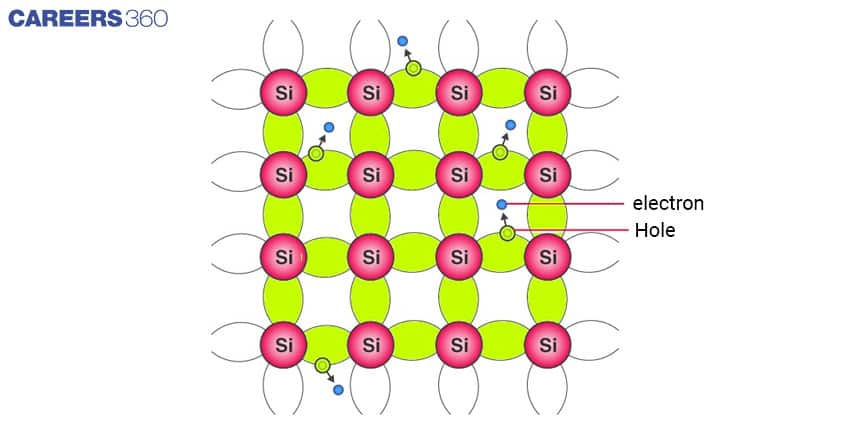
The above figure shows the structure with all bonds intact (i.e. no bonds are broken). This is possible only at low temperatures. As the temperature increases, more thermal energy becomes available to these electrons and some of these electrons may break–away from the conduction band becoming the free electron and creating a vacancy in the bond. This vacancy with an effective positive electronic charge is called a hole.

In intrinsic semiconductors, the number of free electrons ( n_e ) is equal to the number of holes ( n_h )

i.e ne=nh=ni where ni is called intrinsic carrier concentration.

Semiconductors possess the unique property in which, apart from electrons, the holes also move. The free-electron moves completely independently as a conduction electron and gives rise to an electron current, I_e under an applied electric field. while Under an electric field, these holes move towards the negative potential generating hole current (I_h).

Hence, the total current (I) is given as I=Ie+Ih

Apart from the process of generation of conduction electrons and holes, a simultaneous process of recombination occurs in which the electrons recombine with the holes. At equilibrium, the rate of generation is equal to the rate of recombination of charge carriers.

An intrinsic semiconductor will behave like an insulator at T = 0 K. As shown in the below figure., at T = 0 K, the electrons stay in the valence band and there is no movement to the conduction band.

When the temperature increases, at T > 0K, some electrons get excited. These electrons jump from the valence to the conduction band as shown in the below figure.

The conductivity of an intrinsic semiconductor at room temperature is very low. As such, no important electronic devices can be developed using these semiconductors. Hence there is a necessity of improving their conductivity. This can be done by making use of impurities. because when a small amount of a suitable impurity is added to the pure semiconductor, the conductivity of the semiconductor is increased manifold

What is Extrinsic Semiconductor?

An extrinsic semiconductor is a semiconductor doped by a specific impurity which is able to deeply modify its electrical properties, making it suitable for electronic applications. The deliberate addition of a desirable impurity is called doping and the impurity atoms are called dopants. Another term for Extrinsic semiconductors is ‘Doped Semiconductor’.

The size of the dopant and Semiconductor atoms should be the same, to make sure that the amount of impurity added should not change the lattice structure of the semiconductor.

The following types of dopants are used in doping the tetravalent (valency 4) Si or Ge:

(i) Pentavalent (valency 5); like Arsenic (As), Antimony (Sb), Phosphorous (P), etc. This will give an n-type semiconductor

(ii) Trivalent (valency 3); like Indium (In), Boron (B), Aluminium (Al), etc. This will give a p-type semiconductor

What is an n-type Semiconductor?

When a pentavalent impurity is added to an intrinsic or pure semiconductor (silicon or germanium), then it is said to be an n-type semiconductor. Pentavalent impurities such as phosphorus, arsenic, antimony, etc are called donor impurities.

The four valence electrons of each phosphorus atom form 4 covalent bonds with the 4 neighbouring silicon atoms. The free-electron (fifth valence electron) of the phosphorus atom does not involved in the formation of covalent bonds. This shows that each phosphorus atom donates one free electron. Therefore, all the pentavalent impurities are called donors.

So, there is a donor energy level between the valence band and the conduction band. Just below the conduction band.

The number of free electrons depends on the amount of impurity (phosphorus) added to the silicon.

Charge on n-type Semiconductor

Even though an n-type semiconductor has a large number of free electrons, the total electric charge of an n-type semiconductor is neutral.

Conduction in n-type Semiconductor

When voltage is applied to n-type semiconductors as shown in the below figure; then the free electrons move towards the positive terminal of the applied voltage. Similarly, holes move towards the negative terminal of the applied voltage.

In an n-type semiconductor, conduction is mainly because of the motion of free electrons.

because In an n-type semiconductor, the population of free electrons is more whereas the population of holes is less (i.e. n_e >>n_h). In an n-type semiconductor, free electrons are called majority carriers and holes are called minority carriers.

What is a p-type semiconductor?

When the trivalent impurity is added to an intrinsic semiconductor (Si and Ge), then it is said to be a p-type semiconductor. Trivalent impurities such as Boron (B), Gallium (G), Indium(In), Aluminium(Al), etc are called acceptor impurities.

The three valence electrons of each boron atom form 3 covalent bonds with the 3 neighbouring silicon atoms.

For the fourth covalent bond, only the silicon atom contributes one valence electron. Thus, the fourth covalent bond is incomplete with the shortage of one electron. and This missing electron is called a hole.

This shows each boron atom accepts one electron to fill the hole. Therefore, all the trivalent impurities are called acceptors. So there is an acceptor energy level just above the valence band. A small addition of impurity (boron) provides millions of holes.

Charge on the P-Type Semiconductor

Even though p-type semiconductor has a large number of holes, the total electric charge of p-type semiconductors is neutral.

Conduction in p-type semiconductor

When voltage is applied to p-type semiconductor as shown in the below figure; then the free electrons move towards the positive terminal of the applied voltage. Similarly, holes move towards the negative terminal of the applied voltage.

In a p-type semiconductor, conduction is mainly because of the motion of holes in the valence band.

because In a p-type semiconductor, the population of free electrons is less whereas the population of holes is more (i.e n_h >>n_e)

In a p-type semiconductor, holes are called majority carriers and free electrons are called minority carriers.

Number of electrons or holes

The electron and hole concentration in a semiconductor in thermal equilibrium are related as:

n_e × n_h = n_i²

On the increasing temperature, the number of current carriers increases.

The relation is given as ne=nh=AT32e−Eg2KT

where

E_g = Energy gap

K = Boltzmann Constant

T = Temperature in kelvin

Solved Examples Based on Types Of Semiconductor: Intrinsic And Extrinsic Semiconductor

Example 1: The conduction of electricity in intrinsic semiconductors is caused by.

1) The flow of electrons in the Conduction band only

2) The flow of holes in the Valence band only

3) Flow of electrons in the conduction band and flow of holes in the valence band.

4) None of these

Solution:

Intrinsic semiconductor

It is a pure semiconductor

e.g. pure Ge, or Pure Si

wherein

low conductivity

n_e = n_h

At room temperature, a few covalent bonds are broken due to thermal agitation. Thus, some of the valence electrons become free and shift to the valence band, leaving a space in the valence band of the intrinsic semiconductor's crystals. This electron-deficient space is known as a hole and it acts like a positively charged particle.

When an external electric field is applied across the semiconductor, the electrons present in the conduction band move opposite the direction of the electric field while the positive holes in the valence bond move in the direction of the external electric field. The movement of the electrons and holes causes the conduction of electricity in intrinsic semiconductors.

Hence, the answer is the option 3.

Example 2: The probability of electrons to be found in the conduction band of an intrinsic semiconductor at a finite temperature

1) increases exponentially with an increasing band gap

2) decreases exponentially with an increasing band gap

3) decreases with increasing temperature

4) is independent of the temperature and the band gap

Solution:

For an intrinsic semiconductor, at a finite temperature, the probability of electrons existing in the conduction band decreases exponentially with an increasing bandgap (Eg)
The relation is n=n0e−Eq/2k9T

where the Energy band gap
kB= Boltzmann's constant.

Hence, the answer is the option (2).

Example 3: In a semiconductor, the number density of intrinsic charge carriers 27∘C is 1.5×1016/m3. If the semiconductor is doped with an impurity atom, the hole density increases 4.5×1022/m3. The electron density in the doped semiconductor is ×109/m3

1) 5

2) 4

3) 6

4) 3

Solution:

ni=1⋅5×1016/m3nh=4⋅5×1022/m3ne=?

We know that, Intrinsic change carrier density =ni=nhne
ni=nhne1⋅5×1016=4⋅5×1022×ne2⋅25×1032=4⋅5×1022×nene=0.5×1010ne=5×109 m−3

Hence, the answer is option (1).

Example 4: What is the conductivity (in (Ω−m)−1 ) of a semiconductor sample having electron concentration of 5×1018 m−3, hole concentration of 5×1019 m−3, electron mobility of 2.0 m2 V−1 s−1 and hole mobility of 0.01 m2 V−1 s−1 ? (write your answer up to two decimals) (Take charge of electron as 1.6×10−19C )

1) 1.68

2) 1.83

3) 0.59

4) 1.20

Solution:

Electrical Conductivity ( σ )
σ=e(neμc+nhμh)
wherein
ne= electron density nh= hole density μe= mobility of electron μh= mobility of holes
Conductivity σ=e(neμe+nhμh)=1.6×10−19(5×1018×2+5×1019×0.01)=1.6×10−19(1019+0.05×1019)=1.6×1.05=1.68(Ω−m)−1

Hence, the answer is option (1).

Example 5: The ratio of electron and hole currents in a semiconductor is 7/4 and the ratio of drift velocities of electrons and holes is 5/4, then the ratio of concentrations of electrons and holes will be

1) 57
2) 75
3) 2549
4) 4925

Solution:

I=nAevd∴IcIh=ncvcnhvh or nenh=IcIh×vhve=74×45=75

Hence, the answer is the option (2).

Summary

Semiconductors, essential for modern electronics, are materials with properties between conductors and insulators. Intrinsic semiconductors are pure and have equal numbers of free electrons and holes, while extrinsic semiconductors are doped with impurities to enhance their conductivity, creating n-type (more free electrons) or p-type (more holes) semiconductors. Understanding these types explains the foundational principles behind electronic components like transistors and diodes.