Value of g - CGS, FPS, Earth, FAQs

What is acceleration due to gravity ‘g’?

According to Newton’s second law of motion, if a force F acts on a body of mass ‘m’, it produces an acceleration ‘a’ i.e. F=ma.

If this force is due to gravity of earth, then this acceleration produced is called acceleration due to gravity denoted by ‘g’.

F=mg (equation-1)

The value of g on earth changes throughout the globe as it depends on factors like altitude, depth, radius of earth, etc. We will find out the reason behind this in this article later. We will also learn how to calculate the value of g (acceleration due to gravity value )when height or depth of a body w.r.t the surface of the earth changes. By equation-1 we can define g as the force of gravity acting on a body of mass m placed near or on the surface of the earth (i.e. at a nearby height or depth or on the surface of the earth).

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. What is acceleration due to gravity ‘g’?
2. Direction and Unit of ‘g’
3. Relation Between g and G
4. Radius, mass and density of earth
5. Variation of g/factors affecting value of g
6. Thus at centre of earth value of g is zero

Also check-

• NCERT Exemplar Class 11th Physics Solutions
• NCERT Exemplar Class 12th Physics Solutions
• NCERT Exemplar Solutions for All Subjects

Since g=F/m, taking m=1 we get- g=F

g is not a universal constant like G. The value of g varies from planet to planet and therefore the weight of the body which is F=mg is different in different planets. However at the surface of the earth value of g is taken to be 9.8m/s2. Hence if a body is freely falling under the influence of earth’s gravity, the acceleration with which it falls is ‘g’.

The value of g is independent of shape, mass or size of a body. It only depends on the mass of earth and radius of earth (or any planet). Thus if 2 bodies of different masses are allowed to fall from the same height h, it reaches the earth’s surface simultaneously. Look at the picture below, Galileo was the first person to do this experiment by dropping 2 spheres of different masses from the top of Leaning Tower of Pisa and established the fact that both of them reached the surface simultaneously.

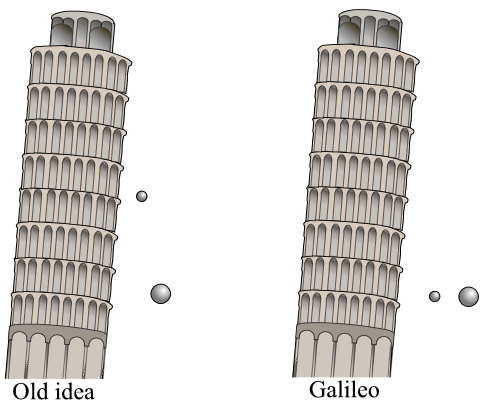
However if 2 bodies have the same masses but different volumes, they will not reach the earth’s surface at the same time because the larger the volume of the body, the larger is the upthrust from air. Hence the body with larger volume will take more time than the body with lower volume to reach the earth’s surface.

Direction and Unit of ‘g’

Acceleration due to gravity ‘g’ is a vector quantity and is always directed towards the centre of the earth. If we consider the freely falling body as the origin in Cartesian coordinates, the direction of g is always towards –Y axis. The S.I. unit of g is m/s2 or N/kg. The dimensional formula for g is M0L1T-2.Value of g in fps (feet per second squared) is 32.1741 feet per second squared.

Relation Between g and G

Let us consider earth to be a sphere of mass M, radius R with the centre of earth as O. Now, if a body of mass m is placed on the surface of earth, g is the acceleration due to gravity acting on it.

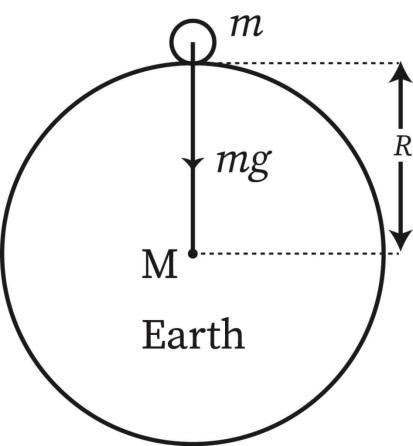(Fig-1)

See the above figure, the force on body of mass m due to earth (mass taken to be M) is-

F=GMm/R2 => mg= GMm/R2 =>g=GM/R2 (equation-2)

From the above equation we can see that the value of g doesn’t depend on mass, size, shape of the body but on mass and radius of the earth.

Radius, mass and density of earth

Now you must be thinking ‘what is the radius of the earth?’ and ‘what is the mass of the earth?’ and how to calculate them.From equation-2 above, we can calculate the mass of the earth. We know that the radius of earth is R=6400km. By equation 2-

M=gR2 /G , where g= 9.8m/s2 and G=6.6710-11Nm2kg-2 - (equation-3)

( unit of gravitation constant in cgs unit is measured in centimeter cube per gram per second square)

Putting the above values, we get M=6.0181024kg

Thus mass of earth in kg is- M=6.0181024kg

Now since we are considering earth to be a spherical body of radius R, then densityρ=MassVolume=M/(43.πR3)=3M/4R3

Then putting equation-3 in equation-2-

ρ=3g4πRG

Putting values of g, G and R, we get- ρ=5.5103kgm-3

Similarly, we can similarly calculate the value of g on mars or value of g on jupiter, if we know the mass and radius of mars and vice versa.

Variation of g/factors affecting value of g

The value of acceleration due to gravity g changes with height, depth and shape of the earth. Let us consider each case and find the formula for g.

a)Effect of altitude(height)- We consider earth to be a sphere of mass M and radius R having centre at O. Let acceleration due to gravity at P (on the surface of earth) be g.

Then, g=GM/R2 (equation-4)

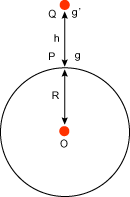(Fig-2)

If acceleration due to gravity at point Q is taken g’, at a height h above the surface of the earth, then-

g’=GM/(R+h)2 (equation-5)

Dividing equation-4 by equation-5, we get-

g’/g=[GM/(R+h)2]×[ R2/GM]

• g’/g=R2/(R+h)2=R2/[R2(1+h/R)2]

• g’/g=(1+h/R)2 (equation-6)

If h<<R, then h/R is small enough as compared to 1 so we can neglect its higher powers. So expanding the above equation-6 through binomial distribution, we get-

g’/g=1- 2h/R => g’=g(1- 2h/R) (equation-7)

Thus from the above equation, we can conclude that the value of g decreases with increase in height h above the surface of earth. That’s why the value of g is lesser at mountains as compared to that on flatlands.

b)Effect of depth- We consider earth to be a homogeneous sphere of mass M and radius R with centre at O. Let g be the acceleration due to gravity at the surface of the earth. Then-

g=GM/R2

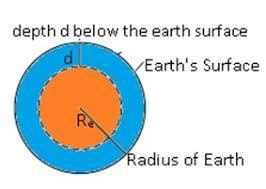(Fig-3)

Let acceleration due to gravity at the depth d be g’. If is the uniform density of earth, then- M=(4/3)πR3

Therefore- g= G×[(4/3)πR3]/ R2 =4/3πGR (equation-8)

Now we need to find the value of g at a point below d distance of earth’s surface. So, the distance of that point from the centre of earth is (R-d). Of course this sphere is smaller than earth. Let its mass be M’ while its density will be the same as we have taken earth to be a homogeneous sphere.

Therefore, g’=GM’/(R-d)2 where M’=4/3(R-d)3 (equation-9)

Now, dividing equation-9 by equation-8, we get-

g’/g=(R-d)/R=1-d/R =>g’=g(1-d/R) (equation-10)

Thus, from the above equation we conclude that acceleration due to gravity decreases with depth.

From (equation-10) we can find the value of g at the centre of the earth. That is-

At centre R=d, then g’=1-R/R=0

Also Read:

• NCERT Solutions for Class 11 Physics Chapter 8 Gravitation
• NCERT Exemplar Class 11 Physics Solutions Chapter 8 Gravitation
• NCERT notes Class 11 Physics Chapter 8 Gravitation

Thus at centre of earth value of g is zero

c)Effect of shape of earth- In both the above cases we have taken earth to be a sphere but in reality it is not a perfect sphere. Its shape is an Oblate spheroid. It bulges out at the equator and flattens at the poles.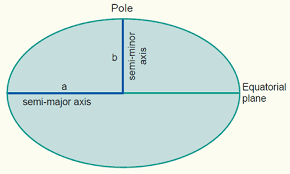(Fig-5)

Hence, the equatorial radius ‘a’ is about 21km larger than the polar radius ‘b’.

Since, g=GM/R2 => g is proportional to 1/R2 as G and M are constants.

And a>b, therefore the value of g is least at equator and keeps increasing towards poles and becomes maximum at poles.

The value of g also varies with rotation of g about its own axis. However we will not cover the derivation in this article.

Also read -

• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for All Subjects

NCERT Physics Notes:

• NCERT Notes Class 11th Physics
• NCERT Notes Class 12th Physics
• NCERT Notes For All Subjects