Application of Percentage: Definition, Formula, Question, Examples

Percentages are a fundamental concept in mathematics, representing a fraction of 100. The term "percent" originates from the Latin phrase "per centum," meaning "by the hundred", and it is denoted by the symbol "%". Percentages are used to express how large or small one quantity is relative to another quantity.

The application of percentage formulas can be seen in a variety of contexts. For example, the use of percentage formula in Excel is a common tool for financial and data analysis. Application of percentage in daily life is immense like calculating tips, tax rates, discounts, and more. Application of percentage questions frequently appears in academic settings, particularly in classes, such as the application of percentages for class 8 and the application of percentages for class 7 or grade 7. Moreover, percentages are crucial in understanding concepts like the application of percentage differential relay in electrical engineering.

Application of Percentage

Percentage is widely used in various fields to express proportions, compare quantities, and analyze data. The applications of percentages are extensive, ranging from everyday situations like shopping discounts to complex analyses in finance, statistics, and scientific research.

Formula used

Application of Percentage in Elections

Specific formula: Percentage of votes = $\frac{\text{Number of votes}}{\text{Total number of votes}} \times 100$%

Example:

In an election, 25% of the votes were found to be invalid. The 1st candidate received 60% of the valid votes and the remaining votes were received by the 2nd candidate. If the difference of votes between them is 15000 votes then find the total number of valid votes.

Let’s understand this problem using a flow chart and solve it.

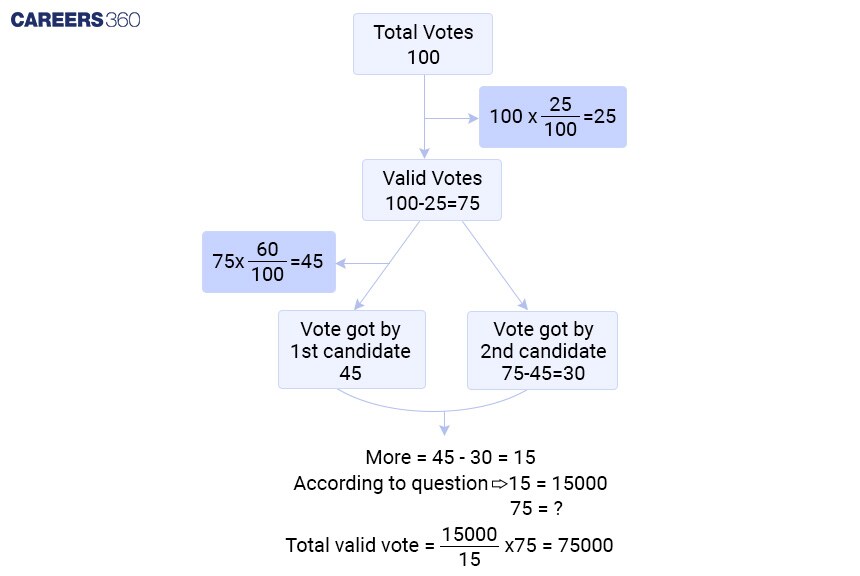
Understanding the terms used in this example:

Application of Percentage in Problems Related to Mixture

Specific formula: Concentration of the substance = $\frac{\text{Amount of the substance}}{\text{Total amount of mixture}} \times 100$%

Example:

A solution contains 36 grams of sugar in 200 grams of water. Find the concentration of sugar in the solution.

Sol: The concentration of sugar in the solution = $\frac{36}{200}\times 100$ = 18%

Application of Percentage in Population

1. Specific formula: Population growth rate = $\frac{\text{Change in population}}{\text{Initial population}} \times 100$%

Example: If a town's population increases from 10,000 to 12,000 in a year, then find the population growth rate.

Sol: The population growth rate = $\frac{12,000-10,000}{10,000}\times 100$ = 20%

2. Specific formula: When the current population is $P$ and the population increases at a rate of $r$% per annum, the population after $n$ years is given by the formula $P(1+\frac{r}{100})^n$.

Example: The present population of the town is 26010. It increases annually at a rate of 2%. What was the population of the town two years ago?

Sol: The present population is $26010$.

The population after $n$ years = $P(1+\frac{r}{100})^n$, where $P$ is the population before two years and the population increases at a rate of $r$% per annum.

So, $P(1+\frac{2}{100})^2 = 26010$

⇒ $P = 25000$

Hence, the correct answer is 25000.

Application of Percentage in Income and Expenditure

Specific formula: Percentage of Savings = $(\frac{\text{Income - Expenditure}}{\text{Total Income}})\times 100$

Example:

If a person earns Rs.50,000 and spends Rs.20,000 monthly, then find his savings percentage.

Sol: Here, Income = Rs.50,000 and Expenditure = Rs. 20,000

So, the savings percentage = $\frac{50000-20000}{50000}\times 100$ = 60%

Another formula: Expenditure = Consumption × Rate

Example:

If the rate of sugar is increased by 10%, then by what percentage a household should reduce its consumption so that expenditure remains constant?

Sol: Let the original rate of sugar be Rs.100/unit and the original consumption is 100 units.
So, the original expenditure = (100 × 100) = Rs.10,000
Now, the rate of sugar is increased by 10%.
So, the new rate of sugar is 100 + 100 × ($\frac{10}{100}$) = Rs.110/unit
Let the new consumption be c units.
Thus the new expenditure = $(110 × c)$ = Rs.$110c$
According to the question,
$110c = 10,000$
⇒ $c = \frac{10,000}{110} = \frac{1000}{11}$
So, the required reduction percentage of consumption
= $\frac{100-\frac{1000}{11}}{100}$ × 100
= $\frac{1100-1000}{11}$
= $9\frac{1}{11}$%

Application of Percentage in Simplification and Approximation

Specific formula: Approximation percentage = $\frac{\text{Estimated value}}{\text{Actual value}}\times 100$

Example:

If 18% of 1150 + 12% of 250 – 35% of 420 = x, then find the value of x.

Sol: x = (10% of 1150 + 8% of 1150) + (10% of 250 + 2% of 250) - (30% of 420 + 5% of 420)

⇒ x = (115 + 92) + (25 + 5) - (126 + 21)

⇒ x = 207 + 30 - 147

⇒ x = 90

Application of Percentage in Examination

Specific formula: Percentage of marks = $\frac{\text{Marks obtained}}{\text{Total marks}}\times 100$

Example:

If a student scores 540 marks out of 600 in an examination, then find the percentage of his marks.

Sol: Here total marks are 600 and the marks obtained by the student are 540.

So, the percentage of marks = $\fraac{540}{600}\times 100$ = 90%

Points to remember

• Percentages are always relative to 100.

• To convert a fraction to a percentage, multiply by 100.

• Percentages can represent increases or decreases in values.

For increased value use (New value - original value).

For decreased value use (Original value - New value).

• Use easy percentages like 10%, 20%, 25%, and 50% as benchmarks.

For example, 10% = $\frac{1}{10}$th of the whole

20% = $\frac{1}{5}$th of the whole

25% = $\frac{1}{4}$th of the whole

• If you know 10%, you can easily find 5% by halving it, or 20% by doubling it.

• For simplification, break down complex problems into simpler parts. For instance, if you need to find 17% of a number, first find 10%, then 5%, and then 2%, and add them together.

Solved Examples

Q.1.

In an election, a candidate secures 40% of the votes but is defeated by the only other candidate by a majority of 298 votes. Find the total number of votes recorded.

1. 1580

2. 1490

3. 1470

4. 1530

Hint: If one candidate received R% of the total votes, the other candidate received (100 – R)% of the total votes.

Solution:

If one candidate received R% of total votes, the other candidates received (100 – R)% of total votes.

Let the total number of votes recorded be $x$.

60% of the votes went to the winning candidate.

According to the question,

(60 – 40)% of $x$ = 298

⇒ 20% of $x$ = 298

⇒ $\frac{x}{5} = 298$

$\therefore x = 1490$

Hence, the correct answer is option (2).

Q.2.

In an election between two candidates, the winning candidate has got 70% of the votes polled and has won by 15400 votes. What is the number of votes polled for the losing candidate?

1. 38500

2. 11550

3. 26950

4. 13550

Hint: If one candidate received R% of the total votes, the other candidate received (100 – R)%.

Solution:

If one candidate received R% of the total votes, then the other candidate received (100 – R)%.

The winning candidate got 70% votes, then the losing candidate got 30% votes.

The candidate won by 15400 votes.

Difference = 70% – 30% = 40% of the votes polled

Given, 40% = 15400 votes,

So, 1% = $\frac{15400}{40}$ = 385 votes

The number of votes received by the losing candidate = 30% of the votes polled

= 30 × 385

= 11550 votes

Hence, the correct answer is option (2).

Q.3.

In a village panchayat society, 574 names are listed as 'below poverty level'. If 14% of the villagers are below the poverty level, the total number of villagers is:

1. 4100

2. 4200

3. 4000

4. 3800

Hint: Let the total population be $x$. According to the question, 14% of $x$ is 574.

Solution:

Let the total population of the village be $x$.

According to the question,

14% of $x=$ 574

⇒ $\frac{x × 14}{100} = 574$

⇒ $x = 4100$

Hence, the correct answer is option (1).

Q.4.

The number of students in a class has increased by 20% and the number has now become 66. Initially, the number was:

1. 45

2. 50

3. 55

4. 60

Hint: Let the initial number of students be $x$. According to the question,

$\frac{120x}{100} = 66$

Solution:

Given: The number of students in a class has increased by 20% and the number has now become 66.

Let the initial number of students be $x$.

According to the question,

⇒ $\frac{120x}{100} = 66$

⇒ $x = 55$

Hence, the correct answer is option (3).

Q.5.

In a marriage party, 32% are women, 54% are men and there are 196 children. How many men are there in the marriage party?

1. 756

2. 448

3. 332

4. 324

Hint: Percentage of children = (100 – 54 – 32)% = 14%

Solution:

Given: 32% of the marriage party are women, 54% are men and there are 196 children.

Percentage of children = (100 – 54 – 32)% = 14%

Here, 14% is equivalent to 196.

⇒ 54% is equivalent to $\frac{196×54}{14}$ = 756

Hence, the correct answer is option (1).

Q.6.

The number of trees in a town is 17640. If the number of trees increases annually at a rate of 5%, how many trees were there two years ago?

1. 14000

2. 15000

3. 16000

4. 19450

Hint: Increased value = $P(1+\frac{r}{100})^n$, where $P$ = present value, $r$ is the rate of percentage increase and $n$ is the number of years.

Solution:

Let the number of trees 2 years ago be $P$.

The number of trees increases annually at a rate of 5%.

The number of trees at present is 17640.

So, $P(1+\frac{r}{100})^n = 17640$

⇒ $P(1+\frac{5}{100})^2 = 17640$

⇒ $P(\frac{21}{20})^2 = 17640$

⇒ $P = 16000$

Hence, the correct answer is option (3).

Q.7.

8 litres of water is added to 32 litres of a solution containing 20% alcohol in water. What is the approximate concentration of alcohol in the solution now?

1. 24%

2. 16%

3. 8%

4. 12%

Hint: Find the amount of alcohol in the solution and then the amount of alcohol in the new solution. Then find the percentage of alcohol in the new solution.

Solution:

The quantity of solution is 32 litres.

Amount of alcohol = $\frac{20}{100}$ × 32 = 6.4 litres

When 10 litres of water is added to the solution, it becomes 32 + 8 = 40 litres

$\therefore$ Percentage of alcohol in the new solution = $\frac{6.4}{40}$ × 100 = 16%

Hence, the correct answer is option (2).

Q.8.

A sugar solution of 3 litres contains 60% sugar. One litre of water is added to this solution. Then the percentage of sugar in the new solution is:

1. 30%

2. 45%

3. 50%

4. 60%

Hint: Find the amount of sugar in the solution and then calculate the required percentage.

Solution:

The quantity of sugar is 3 litres.

Amount of sugar in solution $=\frac{60}{100} × 3 = 1.8$ litres

If 1 litre of water is added, the new solution becomes = 3 + 1 = 4 litres

Percentage of sugar in new solution $=\frac{1.8}{4}×100 = 45\%$

Hence, the correct answer is option (2).

Q.9.

In an examination, 35% of total students failed in Hindi, 45% failed in English and 20% failed in both. Find the percentage of those students who passed in both subjects.

1. 45%

2. 35%

3. 20%

4. 40%

Hint: Find the percentage of students who failed in at least one subject, then subtract that from 100%.

Solution:

Failed in Hindi = 35%

Failed in English = 45%

Failed in both = 20%

$\therefore$ Percentage of students who failed in a minimum of one subject = (35 + 45) – 20 = 60%

Percentage of students who passed in both subjects = (100 – 60) = 40%

Hence, the correct answer is option (4).

Q.10.

A student has to score 40% to pass. He gets 67 and fails by 13 marks. What are the maximum marks?

1. 240

2. 200

3. 150

4. 300

Hint: Let the maximum marks be 100%. Use the concept of percentages to calculate the answer.

Solution:

Let the maximum marks be 100%.

According to the question,

40% marks are equivalent to (67 + 13) = 80 marks

Now, 100% marks are equivalent to $\frac{80×100}{40}$ = 200 marks

So, the maximum marks = 200

Hence, the correct answer is option (2).

Q.11.

Raman spends 80% of his income. If his income is increased by 25% and the expenditure increases by 10%, what will be the percentage increase in his savings?

1. 17%

2. 70%

3. 77%

4. 85%

Hint: Let Raman's income be Rs. 100. Then, use this formula:

Percentage change = $\frac{\text{Difference}}{\text{Initial value}} × 100$

Solution:

Let Raman's income be Rs. 100.

Raman spends 80% = $\frac{80}{100}× 100$ = Rs. 80

Raman's savings = 100 – 80 = Rs. 20

If his income is increased by 25%,

New income $=\frac{125}{100} × 100 = 125$

If his expenditure increases by 10%,

New expenditure $=(\frac{110}{100}) × 80 = 88$

New savings = 125 – 88 = Rs. 37

The increase in savings is (37 – 20) = Rs. 17

Percentage change = $\frac{\text{Difference}}{\text{Initial value}} × 100$

Percentage increase in savings $=\frac{17}{20} × 100 = 85$%

Hence, the correct answer is option (4).

Q.12.

A man spends 60% of his income on different items. His income has increased by 20% and his expenditure has also increased by 10%. Find the percentage increase in his savings.

1. 10%

2. 15%

3. 20%

4. 35%

Hint: Assume that the total salary of a man is 100 units and use the formula:

Savings = Income – Expenditure

Solution:

Let's assume the total salary of a man = 100 units

Expenditure on different items = 60 units

Savings of the man = (100 – 60) = 40 units

New income of man increased by 20% = 100 × $\frac{120}{100}$ = 120 units

His new expenditure also increases by 10% = 60 × $\frac{110}{100}$ = 66 units

New savings of the man = (120 – 66) = 54 units

Difference in savings = (54 – 40) = 14 units

Percentage increase in savings $=\frac{14}{40} × 100 = 35\%$

Hence, the correct answer is option (4).

Q.13.

A reduction of 21% in the price of an item enables a person to buy 3 kg more for Rs. 100. The reduced price of the item per kg is:

1. Rs.5.50

2. Rs.7.50

3. Rs.10.50

4. Rs.7.00

Hint: Let the original price be Rs. $100x$. After the 21% reduction, the price dropped by Rs. $21x$.

Rs. $21x$ is also the cost of 3 kg more.

Solution:

Given: A reduction of 21% in the price of an item enables a person to buy 3 kg more for Rs. 100.

Let the original price be Rs. $100x$. After the 21% reduction, the price dropped by Rs. $21x$.

Rs. $21x$ is also the cost of 3 kg more.

Now, Rs. $100x$ will enable a purchase of ($\frac{3×100x}{21x}$) = $\frac{100}{7}$ kg more.

So, we get $\frac{100}{7}$ kg for Rs. 100

Therefore, the reduced price of the item per kg is = 100 × $\frac{7}{100}$ = Rs. 7

Hence, the correct answer is Rs. option (4).

Q.14.

The number that is to be added to 10% of 320 to have the sum as 30% of 230 is:

1. 37

2. 32

3. 23

4. 73

Hint: Use the concept of percentages, $x$% of y = $\frac{x×y}{100}$

Solution:

To find: The number that is to be added to 10% of 320 to have the sum as 30% of 230.

Here, 10% of 320 = $\frac{10}{100}$ × 320 = 32

and 30% of 230 = $\frac{30}{100}$ × 230 = 69

Therefore, the number to be added is = (69 – 32) = 37

Hence, the correct answer is option (1).

Q.15.

A village lost 12% of its goats in a flood and 5% of the remainder died from diseases. If the number left now is 8360, what was the original number before the flood?

1. 1000

2. 10,000

3. 1,00,000

4. 3860

Hint: Let the original number of goats before the flood be 100 units. Calculate how many were lost and how many died. The remaining units are equivalent to 8360.

Solution:

Given: A village lost 12% of its goats in a flood and 5% of the remainder died from diseases.

Let the original number be 100 units.

12% of goats were lost in the flood ⇒ (100×$\frac{12}{100}$) = 12 units were lost.

Now, the remaining goats = (100 – 12) = 88 units

5% of the remainder died from diseases = (88×$\frac{5}{100}$) = 4.4 units

The number of goats left = (88 – 4.4) = 83.6 units

Here, 83.6 units are equivalent to 8360

⇒ 100 units are equivalent to ($\frac{8360}{83.6}$ × 100) = $\frac{8360000}{836}$ = 10,000 goats

So, the original number of goats is 10,000.

Hence, the correct answer is option (2).