Application of TSD in Trains and Stream: Meaning, Questions, Examples

Understanding the concepts of Time, Speed, and Distance (TSD) is crucial for solving various real-life problems involving motion. These concepts are widely used in problems related to trains, boats, and streams, where the notion of relative speed often comes into play, which is the speed of one object as observed from another moving object. In this article, we will discuss ‘TSD in Trains and Streams’, ‘TSD full form’, ‘TSD meaning’ etc.

Problems on Trains: Concept

Problems involving trains typically focus on calculating the time taken to cross a certain distance, which may include stationary objects, other trains, or platforms. There are many different types of problems related to trains, let us discuss them one by one with proper examples.

Types of problems

• A train crosses a stationary object

When a train crosses a stationary object (like a pole or signal), the distance covered by the train is equal to the length of the train.

Formula: Time taken to cross a stationary object = $\frac{\text{Length of the train}}{\text{Speed of the train}}$

Example: A train covers a distance of 12 km in 10 minutes. If it takes 6 seconds to pass a telegraph post, then find the length of the train.

Solution: A train covers a distance of 12 km in 10 minutes.

The time taken by the train to pass a telegraph post is 6 seconds.

The speed of the train = $\frac{12×1000}{10×60}$ m/s = 20 m/s

Length of the train = Speed of the train × Time taken by the train to pass a telegraph post

$\therefore$ Length of the train = 20 × 6 = 120 m

Hence, the correct answer is 120 m.

• Two trains crossing each other when moving in opposite directions

When two trains move in opposite directions, their relative speed is the sum of their individual speeds.

Formula: Time taken by a train to cross another train = $\frac{\text{Sum of the length of the trains}}{\text{Sum of the speed of the trains}}$

Example: A train of length 100 metres crosses another train of length 150 metres, running on a parallel track in the opposite direction, in 9 seconds. If the speed of a train having a length of 150 metres is 40 km/h, then what is the speed (in km/h) of the other train?

Solution:

Length of 1st train = 100 m

Length of 2nd train = 150 m

Speed of 2nd train = 40 km/h

Formula used:

Time taken to cross the train = $\frac{\text{Sum of length of trains}}{\text{Their relative speed}}$

Calculation:

The relative speed = $\frac{100+150}{9} = \frac{250}{9}$m/s $= \frac{250 \times 18}{9 \times 5} = 100$ km/h

When two trains are running in opposite directions their relative speed is the sum of their speed.

⇒ 100 = 40 + Speed of other train

$\therefore$ Speed of other train $= 100 - 40 = 60$ km/h

Hence, the correct answer is 60 km/h.

• The faster train crosses the slower train

When a faster train overtakes a slower train moving in the same direction, their relative speed is the difference in their speeds.

Formula: Time taken by a train to cross another train = $\frac{\text{Sum of the length of the trains}}{\text{Relative speed of the trains}}$

Example: Train B, speeding at 100 km/hr, crosses another train C, running in the same direction, in 2 minutes. If the lengths of trains B and C are 150 metres and 250 metres, respectively, what is the speed of train C (in km/h)?

Solution: Let the speed of train C be $x$ km/hr.

$\therefore$ Relative speed of B = $(100 - x )$ km/hr

$\therefore$ Time taken to cross = $\frac{\text{Length of both trains}}{\text{Relative speed}}$

⇒ $\frac{2}{60} = \frac{\frac{150+250}{1000}}{100-x}$

⇒ $\frac{1}{30} = \frac{2}{5(100-x)}$

⇒ 100 – $x$ = 12

$\therefore x$ = 88 km/hr

Hence, the correct answer is 88.

• A train crosses a platform

When a train crosses a platform, the distance covered is the sum of the length of the train and the length of the platform.

Formula: Time taken by a train to cross a platform = $\frac{\text{Sum of the length of the train and the length of the plateform}}{\text{Speed of the train}}$

Example: A train passes by a lamp post on a platform in 7 seconds and passes by the platform completely in 28 seconds. If the length of the platform is 390 m, then find the length of the train (in metres).

Solution: Length of the platform = 390 m

The time taken to cross a lamp post is 7 seconds.

The time taken to cross the platform is 28 seconds.

Let the length of the train be $x$ m.

Speed of the train = $\frac{\text{Distance}}{\text{Time}}$ = $\frac{x}{7}$ m/s

Length of the train + Length of the platform = Speed of train × Time

$⇒ x + 390 = \frac{x}{7} \times 28$

$⇒ x+390=4x$

$⇒ 3x=390$

$\therefore x=130$ m

Hence, the correct answer is 130.

• Meeting time of two trains

When two trains start from different points and move towards each other, the time taken to meet is determined by their relative speed and the initial distance between them.

Formula: Meeting time of the trains = $\frac{\text{Sum of the length of the trains}}{\text{Relative speed of the trains}}$

Example: Train X and Train Y start at 6 AM from two stations 600 km apart and move towards each other at speeds of 50 km/hr and 100 km/hr respectively. Calculate the time when the two trains meet.

Solution: Here, the relative speed of two trains = (50 + 100) = 150 km/hr

Now, the required time = $\frac{\text{Distance}}{\text{ Relative speed}}$

= $\frac{600}{150}$

= 4 hours.

So, the two trains will meet after 4 hours.

Therefore, they will meet at (6 + 4) = 10 AM.

• Distance Covered When Two Trains are Moving in the Same/Opposite Direction

When two trains are moving in the same or opposite direction, the distance covered is given as Distance = Relative Speed × Time.

Example: Two trains start from a certain place on two parallel tracks and in the same direction. The speeds of the trains are 45 km/hr and 40 km/hr respectively. Find the distance between the two trains after 45 minutes.

Solution: Given: The speeds of the trains are 45 km/hr and 40 km/hr.

The relative speed = (45 – 40) = 5 km/hr = 5 × $\frac{5}{18}$ m/s = $\frac{25}{18}$ m/s

Distance travelled after 45 minutes = $\frac{25}{18}$ × 45 × 60 = 3750 m = 3 km 750 m

Hence, the correct answer is 3 km 750 m.

• Important formulas

Important points regarding problems with trains

• Relative Speed of Trains Moving in the Same Direction

Relative speed = Speed of faster train - Speed of slower train

• Relative Speed of Trains Moving in Opposite Directions

Relative speed = Sum of speeds of both trains

• Distance Covered When Two Trains are Moving in the Same/Opposite Direction

Distance = Relative Speed × Time

• Distance Travelled When a Train Crosses a Stationary Object

Distance = Length of the train

• Distance Travelled When a Train Crosses a Platform/Bridge

Distance = Length of the train + Length of the platform/bridge

Boat and Stream: Concept

The movement of a boat in a river is determined by the speed of the water current i.e. the stream. The speed of the boat in still water and the speed of the stream together give the effective speed of the boat either downstream or upstream.

• Speed of boat in still water (B): The speed of a boat in still water is the speed at which the boat would travel if there were no currents or streams.

• Speed of stream (S): The speed of the stream, refers to the velocity of the water current in a river or any other flowing body of water. This speed affects the movement of boats or swimmers, either aiding or opposing their progress depending on the direction of travel.

• Downstream speed (D): Downstream speed is the effective speed of a boat or swimmer when moving in the direction of the current. It is calculated by adding the speed of the boat (B) in still water to the speed of the stream or current (S).
  Downstream Speed (D) = Speed of Boat in Still Water (B) + Speed of Stream (S).

• Upstream speed (U): Upstream speed is the effective speed of a boat when it moves against the direction of the water current. It is calculated by subtracting the speed of the stream (S) from the speed of the boat in still water (B).
  Upstream Speed (D) = Speed of Boat in Still Water (B) - Speed of Stream (S).

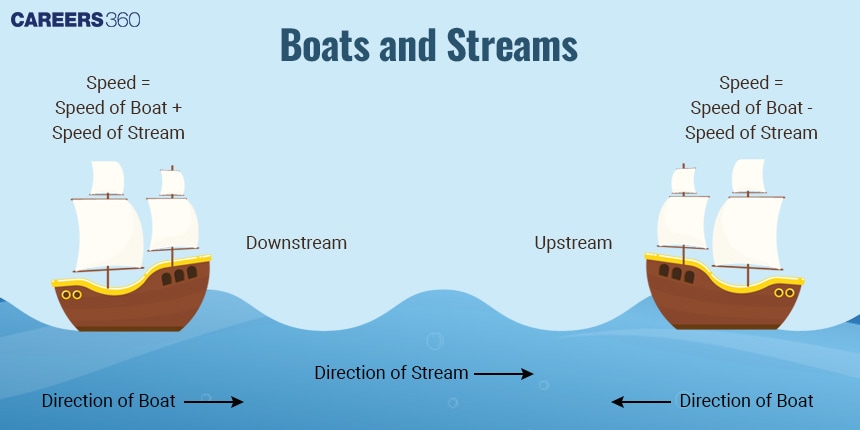
Upstream and Downstream: Important formulas

Types of problems

• Time-Based Questions

Example: If the speed of a boat in still water is 20 km/hr and the speed of the current is 5 km/hr, then find the time taken by the boat to travel 100 km with the current.

Solution: Distance = 100 km

Speed of boat in still water = 20 km/hr

Speed of current = 5 km/hr

The speed of the boat with the current = Speed of boat in still water + Speed of current

= 20 + 5 = 25 km/hr

Time taken by boat = $\frac{\text{Distance}}{\text{Speed}}$ = $\frac{100}{25}$ = 4 hours

Hence, the correct answer is 4 hours.

• Speed-Based Questions

Example: A boat moves downstream at a rate of 8 km/hr and upstream at 4 km/hr. Find the speed of the boat in still water.

Solution: A boat moves downstream at a rate of 8 km/hr and upstream at 4 km/hr.

We know, the speed of the boat in still water

$=\frac{\text{(Downstream speed + Upstream speed)}}{2}=\frac{(8+4)}{2}=\frac{12}{2}$ = 6 km/hr

Hence, the correct answer is 6 km/hr.

• Questions on Average Speed

Example: A boat covers a distance of 72 km downstream in 8 hours, while it takes 10 hours to cover the same distance upstream. Find the average speed of the boat.

Solution: Total distance covered = (72 + 72) = 144 km

Total time taken = (8 + 10) = 18 km/hr

So, the average speed = $\frac{\text{Total distance}}{\text{Total time}}$

= $\frac{144}{18}$

= 8 km/hr

Hence, the average speed of the boat in the whole journey is 8 km/hr.

• Questions Based on Distance

Example: A boat can cover 120 km upstream and back in a total of 30 hours, and 25 km upstream and 40 km downstream in a total of 7 hours. How much distance will the boat cover in 16 hours in still water?

Solution: Let the speed of the boat in still water be $x$ km/hr and the speed of the current be $y$ km/hr.

Speed downstream = $x + y$

Speed upstream = $x - y$

Now, $\text{Time} = \frac{\text{Distance}}{\text{Speed}}$

$\frac{120}{x + y} + \frac{120}{x - y} = 30$....(1)

and$\frac{40}{x + y} + \frac{25}{x – y} = 7$ ....(2)

Multiplying equation (2) by 3, we get,

$\frac{120}{x + y} + \frac{75}{x – y} = 21$ ......(3)

Subtracting equation (3) from (1), we get,

$\frac{45}{x – y} = 9$

$⇒x - y = 5$.......(4)

Putting the value of $x - y$ in equation (2), we get,

$x + y = 20$ .......(5)

Solving these two equations, we get the values of $x$ and $y$.

$x = 12.5$ and $y = 7.5$

Distance covered by the boat in 16 hours in still water = 16 × 12.5 = 200 km

Hence, the correct answer is 200 km.

Tips and Tricks (Problems on Trains, Boat and Stream)

• Convert speeds to the same units before performing calculations.

• Use relative speed for trains moving in the same or opposite directions.

• Memorize key formulas for different types of problems to save time.

• Add the lengths of the train and the object (like another train or platform) to get the total distance covered.

• Draw simple diagrams to visualise the problem and the movement of trains or boats.

Practice Questions/Solved Examples

Q.1.

A train is running at a speed of 116 km/hr. The distance covered by the train (in metres) in 18 seconds is:

1. 2

2. 2

3. 2

4. 2

Hint: Use the given formula:

Distance = Speed × Time

Solution:

Given: The speed of the train is 116 km/hr.

For converting it into m/sec, multiply with $\frac{5}{18}$.

So, 116 km/hr = 116 × $\frac{5}{18}$ m/s = $\frac{580}{18}$ m/s

$\therefore$ The distance covered in 18 seconds = Speed × Time = $\frac{580}{18}×18=580$ metres

Hence, the correct answer is 580 metres.

Q.2.

A train passes two bridges of lengths 400 metres and 200 metres in 80 seconds and 60 seconds, respectively. What is the length (in metres) of the train?

1. 200

2. 400

3. 350

4. 750

Hint: Use this formula:

$\text{Speed}=\frac{\text{Distance}}{{\text{Time}}}$

Solution:

Let the speed of the train be $y$ m/s and the length of the train be $x$ metres.

$\text{Speed}=\frac{\text{Distance}}{{\text{Time}}}$

Case – 1:

Total distance = ($x+400$) m

Time = 80 seconds

$y=\frac{x+400}{80}$ ---(1)

Case – 2:

Total distance = ($x+200$) m

Time = 60 seconds

$y=\frac{x+200}{60}$ ---(2)

From equation (1) and (2), we get,

$\frac{x+400}{80}=\frac{x+200}{60}$

⇒ $3x+1200=4x+800$

$\therefore x = 400$

Hence, the correct answer is 400 metres.

Q.3.

Two trains 100 metres and 95 metres long, respectively pass each other in 27 seconds when they run in the same direction and in 9 seconds when they run in opposite directions. The speeds of the two trains are:

1. 44 km/hr, 22 km/hr

2. 52 km/hr, 26 km/hr

3. 36 km/hr, 18 km/hr

4. 40 km/hr, 20 km/hr

Hint: Relative speed when both trains running in the same direction = speed of faster train – speed of slower train

Relative speed when both trains running in the opposite direction = speed of faster train + speed of slower train

Solution:

Let the speed of the first train be $x$ km/hr and the speed of the second train is $y$ km/hr.

Time = $\frac{\text{Total distance}}{{\text{Relative speed in same/Opposite direction}}}$

In the same direction,

⇒ $27=\frac{100+95}{(x-y)×\frac{5}{18}}$

⇒ $27=\frac{195×18}{5(x-y)}$

⇒ $x-y=26$ ----------------(i)

In the opposite direction,

⇒ $9=\frac{100+95}{(x+y)×\frac{5}{18}}$

⇒ $9=\frac{195×18}{5(x+y)}$

⇒ $x+y=78$ ------------------(ii)

Solving equation (i) and (ii), we get,

$x=52,$ and $y=26$

Hence, the correct answer is 52 km/hr and 26 km/hr.

Q.4.

Two trains start from stations A and B and travel towards each other at speeds of 16 miles/hour and 21 miles/hour, respectively. At the time of their meeting, the second train had travelled 60 miles more than the first. The distance between A and B (in miles) is:

1. 444 miles

2. 496 miles

3. 333 miles

4. 540 miles

Hint: Assume the time at which the trains meet is $x$ hours. Then use the formula below.

$\text{Distance} = \text{Speed}\ ×\ \text{Time}$

Solution:

Let the time at which the trains meet be $x$ hours.

The distance covered by the first train at this time is $16x$ miles and the distance covered by the second train is $21x$ miles.

The second train has travelled 60 miles more than the first.

So, $21x -16x = 60$

$⇒5x = 60$

$⇒x = \frac{60}{5}$

$\therefore x= 12$

So, the trains meet 12 hours after they start.

The total distance between A and B is the sum of the distances travelled by both trains.

$\therefore 16x + 21x = (16 + 21) \times 12 = 37 \times 12 = 444$ miles

Hence, the correct answer is 444 miles.

Q.5.

A boat goes 4 km upstream and 4 km downstream in an hour. The same boat goes 5 km downstream and 3 km upstream in 55 minutes. What is the speed (in km/hr) of the boat in still water?

1. 6.5

2. 7.75

3. 10

4. 9

Hint: Assuming the speed of the boat in still water is $a$ km/hr, the speed of water is $b$ km/hr.

Speed in downstream = $a+b$

Speed in upstream = $a-b$

Solution:

Let the speed of the boat in still water be $a$ km/hr and the speed of water be $b$ km/hr.

Speed in downstream = $a+b$

Speed in upstream = $a-b$

As per the first given condition:

$⇒ \frac{4}{(a-b)}+\frac{4}{(a+b)}=1$

Let $\frac{1}{(a-b)}=x$ and $\frac{1}{(a+b)}=y$

$⇒4x+4y=1$

$⇒ x+y =\frac{1}{4} $ --------------------------(1)

As per the second given condition:

$⇒\frac{3}{(a-b)}+\frac{5}{(a+b)}=\frac{55}{60}$

$⇒3x+5y=\frac{11}{12}$

By putting the value of $y$ from equation (1) we get:

$⇒3x+5(\frac{1}{4}-x)=\frac{11}{12}$

$⇒2x=\frac{5}{4}-\frac{11}{12}$

$⇒x=\frac{1}{6}⇒(a-b)=6$ ----------------------------(2)

By putting the value of $x$ in equation (1)

$⇒y=\frac{1}{4}-\frac{1}{6}$

$⇒y=\frac{1}{12}⇒(a+b)=$ 12 --------------------(3)

From equation (2) and (3),

$⇒2a= 18⇒a= 9$

The speed of the boat in still water is 9 km/hr.

Hence, the correct answer is 9.

Q.6.

Dharmendra can row 80 km upstream and 110 km downstream in 13 hours. Also, he can row 60 km upstream and 88 km downstream in 10 hours. What is the speed (in km/hr ) of the current?

1. 6

2. 16

3. 10

4. 12

Hint: Speed of the current = $\frac{1}{2}$ × (Downstream speed – Upstream speed)

Solution:

Let downstream speed and upstream speeds be $u$ km/hr and $v$ km/hr, respectively.

Dharmendra can row 80 km upstream and 110 km downstream in 13 hours

$\frac{110}{u}+\frac{80}{v}=13$..................(I)

He can row 60 km upstream and 88 km downstream in 10 hours.

$\frac{88}{u}+\frac{60}{v}=10$..................(II)

Equation (I) is multiplied by 3 and equation (II) is multiplied by 4.

We get,

$\frac{330}{u}+\frac{240}{v}=39$..................(III)

$\frac{352}{u}+\frac{240}{v}=40$..................(IV)

Subtracting equation (III) from equation (IV), we get,

$\frac{22}{u}=1$

⇒ $u=22$ km/hr

Putting $u = 22$ in equation (I), we get,

$\frac{110}{22}+\frac{80}{v}=13$

⇒$\frac{80}{v}=8$

⇒$v=10$ km/hr

Speed of the current = $\frac{1}{2}$ × (Downstream speed – Upstream speed)

= $\frac{1}{2}$ (22 – 10) = 6 km/hr

Hence, the correct answer is 6.

Q.7.

A boat covers a distance of 12 km in 1 hour upstream and 45 minutes downstream. Find the speeds of the boat and the stream (in km/hr).

1. 16 and 4

2. 16 and 2

3. 14 and 2

4. 12 and 4

Hint: Downstream Speed = Speed of the boat + Speed of the stream

Upstream Speed= Speed of the boat – Speed of the stream

Solution:

Let the speed of the boat be x km/hr and the speed of the stream be y km/hr.

So, downstream speed = x + y = $\frac{12×60}{45}=16$ km/hr............(1)

Upstream speed= x – y = 12 km/hr...........(2)

By solving the above equations, we get,

$\therefore$ Speed of the boat = $\frac{16+12}{2}=14$ km/hr

$\therefore$ Speed of the stream = $(16 - 14) = 2$ km/hr

Hence, the correct answer is 14 and 2.

Q.8.

A train 270 m long, is running at a speed of 36 km/hr, then it will cross a bridge of length 180 m in:

1. 40 sec

2. 45 sec

3. 50 sec

4. 35 sec

Hint: First, convert speed in km/hr into m/s, then use the formula: Time taken = $\frac{\text{Distance}}{\text{Speed}}$ to solve this.

Solution:

Speed = 36 km/hr = 36 × $\frac{5}{18}$ = 10 m/s

Distance = 270 + 180 = 450 m

$\therefore$ Time taken = $\frac{\text{Distance}}{\text{Speed}}=\frac{450}{10}$ = 45 sec

Hence, the correct answer is 45 sec.

Q.9.

Two trains, 80 m and 120 m long, are running at the speeds of 25 km/hr and 35 km/hr, respectively in the same direction on parallel tracks. How many seconds will they take to pass each other?

1. 48

2. 64

3. 70

4. 72

Hint: First, find the relative speed. Then, use the formula: Time = $\frac{\text{Sum of the length of the trains}}{\text{Relative Speed}}$ to solve this.

Solution:

Distance to be covered = 80 + 120 = 200 m

Relative speed = 35 – 25 = 10 km/hr = 10 × $\frac{5}{18}$ = $\frac{50}{18}$ m/s

$\therefore$ Time taken to pass = $\frac{\text{Sum of the length of the trains}}{\text{Relative Speed}}=\frac{200}{\frac{50}{18}}$ = 72 seconds

Hence, the correct answer is 72 seconds.

Q.10.

The speed of the boat down the stream is 125% of the speed in still water. If the boat takes 30 minutes to cover 20 km in still water, then how much time (in hours) will it take to cover 15 km upstream?

1. $\frac{3}{4}$

2. $\frac{1}{2}$

3. $\frac{1}{4}$

4. $1$

Hint: The speed of the boat downstream = 125% of the speed of the boat in still water.

Speed of boat upstream = speed of boat in still water – speed of current

Solution:

Speed of boat in still water = $\frac{20}{\frac{30}{60}}= 40$ km/hr

Speed of boat downstream = $50$ km/h (As it is $125$% more than the speed of the boat in still water)

Speed of current = $50 - 40$ = $10$ km/hr

The time it will take to cover $15$ km upstream

$=\frac{\text{Distance}}{\text{Speed in still water – speed of current}}=\frac{15}{30} = \frac{1}{2}$ hour

Hence, the correct answer is $\frac{1}{2}$.