Arithmetic Progression: Definition, Formulas, Sum and Examples

An arithmetic progression (AP) is a sequence of numbers in which the difference between any two consecutive terms is the same. For example, 2, 4, 6, 8, 10,....... is an arithmetic progression, where the difference between any two consecutive numbers is 2.

A real-life example of an AP is the sequence formed by the annual income of an employee whose income increases by a fixed amount of Rs.1000 every year. So, after 8 years his income will increase by Rs.8000.

In this article, we will talk about various aspects of AP like ‘arithmetic progression formula’, ‘arithmetic progression’, ‘arithmetic progression examples’, ‘sum of arithmetic progression’, ‘arithmetic progression questions’, ‘formula of arithmetic progression’, ‘arithmetic progression sum formula’ etc.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. What is Arithmetic Progression (AP)?
2. Terms and Notations Used in Arithmetic Progression:
3. The general term of an AP ($t_n$)
4. Types of AP
5. The sum of n terms of an AP:
6. Arithmetic Mean (AM)
7. Important Properties of an AP
8. Tips and Tricks
9. Solved Examples Based on Arithmetic Progression
10. Summary

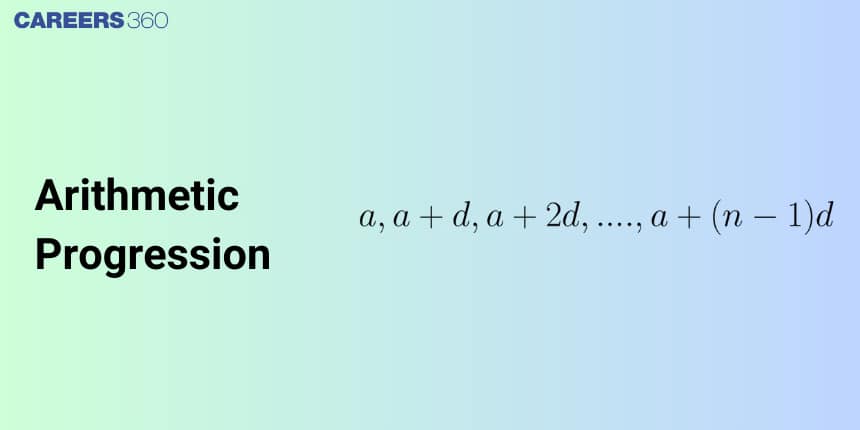
What is Arithmetic Progression (AP)?

An arithmetic progression (AP) is a mathematical sequence of numbers where the difference between any two consecutive terms is constant. In this progression, each term, except the first term, is obtained by adding a fixed number to its previous term. This fixed term is called the common difference. For example, 1, 5, 9, 13, ……. is an arithmetic progression where the common difference is (5 - 1) = (9 - 5) = (13 - 9) = 4.

Comparison with Geometric Progression and Harmonic Progression

Terms and Notations Used in Arithmetic Progression:

In Arithmetic Progression (AP), several terms and notations are commonly used to describe and calculate the sequence. These terms and notations are as follows:

First term ($a_1$ (or) $a$):

As the name suggests, the first term of an AP is the first number of the progression. It is usually represented by $a_1$ (or) $a$. For example, in the AP 5, 10, 15, 20, ….. the first term $a$ is 5.

Common difference (d):

In Arithmetic Progression, each term, except the first term, is obtained by adding a fixed number to its previous term. This fixed term is called the common difference. It is usually denoted by $d$. If $a$ is the first term of an AP and $d$ is the common difference, then the AP will be:

$a, (a+d), (a+2d), (a+3d), (a+4d),....$

For example, 4, 10, 16, 22, ….. is an AP where the first term is 4 and the common difference is

(10 - 6) = (16 - 10) = (22 - 16) = 6.

The number of terms (n):

As the name suggests, the number of terms of an AP is the total number of terms present in the progression or in the sequence. It is usually denoted as $n$.

For example, 1, 2, 3, 4, 5 is an example of an AP where the number of terms ($n$) is 5.

The general term of an AP ($t_n$)

The general term or the nth term of an arithmetic sequence can be expressed in two ways i.e. the nth term of an AP from the beginning and the nth term of an AP from the last. We will discuss these two ways below.

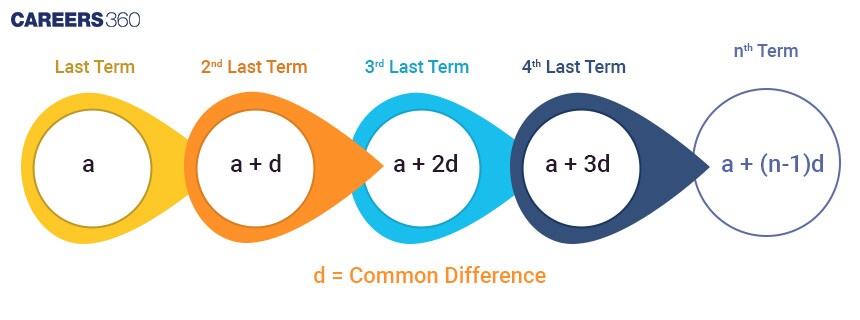
The nth term of an AP from the beginning:

The general term of the nth term from the beginning of an AP where the first term is $a$, the common difference is $d$, and the number of terms is $n$ is given by the formula:

$t_n = a + (n - 1)d$.

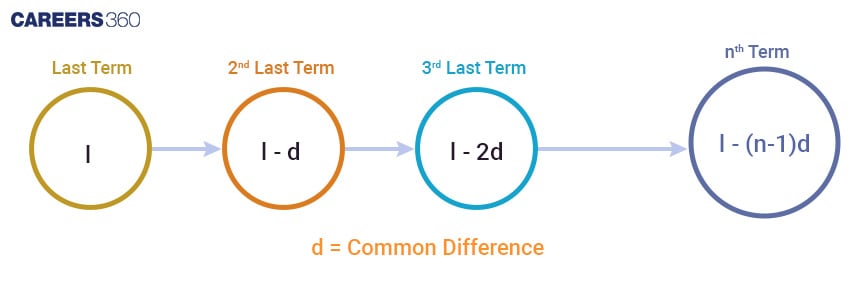
The nth term of an AP from the last:

The nth term of an AP from the last, where the last term is $l$, the common difference is $d$, and the number of terms is $n$, is given by the formula:

$t_n = l - (n - 1)d$.

The nth term of an AP if the mth term is given but the first term is not given:

The mth term of an AP is given.

So, $t_m=a+(m-1)d$, where $a$ is the first term and $d$ is the common difference.

Since the first term is not given, we need to find the first term in terms of the given mth term.

So, $a = t_m - (m-1)d$

Now, for the nth term,

$t_n = a+(n-1)d = t_m - (m-1)d + (n-1)d = t_m - md + d + nd - d = t_m + (n-m)d$

Therefore, $t_n = t_m + (n - m)d$ is the required nth term of an AP when the mth term is given but the first term is not given.

The sum of Arithmetic progressions

The sum, Sn of n terms of an AP with the first term ‘a’ and common difference ‘d’ is given by

$\begin{aligned} & S_n=\frac{n}{2}[2 a+(n-1) d] \\ & \text { OR } \\ & S_n=\frac{n}{2}[a+l] \\ & a \rightarrow \text { first term } \\ & d \rightarrow \text { common difference } \\ & n \rightarrow \text { number of terms }\end{aligned}$

Types of AP

There are mainly two types of arithmetic progressions, categorized based on their properties and applications. One is Finite AP and the other one is Infinite AP. For better understanding let us discuss them in detail.

Finite AP:

The Finite AP is a sequence with a finite number of terms. The first term, last term, common difference, and the number of terms can be identified from the series.

For example, 2, 4, 6, 8, 10 is a finite AP, where the first term $a$ = 4, the last term $l$ = 10, the common difference $d$ = 10 - 8 = 8 - 6 = 6 - 4 = 4 - 2 = 2, and the number of terms $n$ = 5.

Infinite AP:

The Infinite AP is a sequence with an infinite number of terms, that continues indefinitely. The first term and the common difference can be identified from the sequence but the number of terms and the last term are unknown.

For example, 3, 6, 9, 12, 15, ….. is an Infinite AP, where the first term $a$ = 3, the common difference $d$ = 15 - 12 = 12 - 9 = 9 - 6 = 6 - 3 = 3, but the last term ($l$) and the number of terms ($n$) are unknown.

Decreasing AP:

An arithmetic progression is decreasing if the common difference $d$ is negative. This means that each term is smaller than the previous term.

For example, 10, 8, 6, 4, 2, …. is a decreasing AP.

Increasing AP:

An arithmetic progression is increasing if the common difference $d$ is positive. This means that each term is larger than the previous term.

For example, 2, 3, 4, 5, ….. is an increasing AP.

The sum of n terms of an AP:

In the 19th century in Germany, a Math class for grade 10 was going on. The teacher asked the students to find the sum of all numbers from 1 to 100. While the students were struggling with the calculations, one boy quickly called out the correct answer as 5050. This boy was none other than the great German mathematician Carl Friedrich Gauss. How did he arrive at the sum so quickly?

Gauss observed that pairing the numbers from the beginning and the end of the sequence resulted in sums that were constant. Specifically, he paired the first number with the last, the second number with the second last, and so on. Each pair had the same sum.

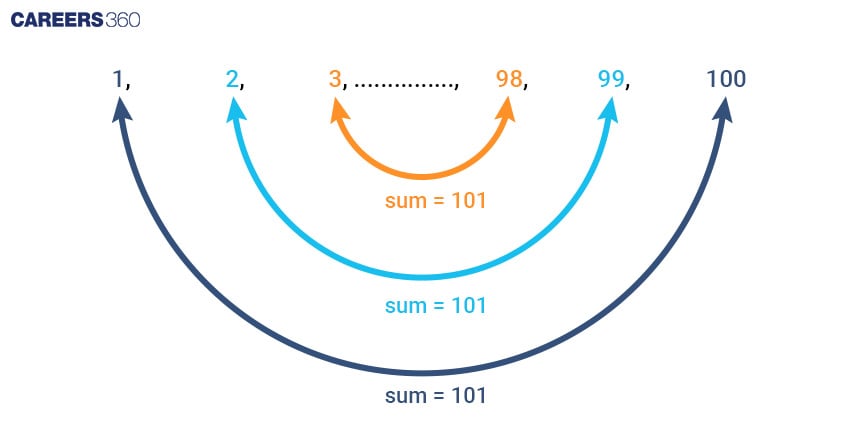
We can see that in sequences 1, 2, 3, ..., 100, there are 50 such pairs whose sum is 101. Thus, the sum of all terms of this sequence is 50 × 101 = 5050.

The sum of n terms of an AP can be calculated using two formulas, let us have a clear understanding of them.

The sum of AP when the last term is not given:

When the last term of the AP is not given we can calculate the sum of the terms of an AP by using the formula:

$S_n = \frac{n}{2}[2a+(n-1)d]$, where $a$ is the first term, $d$ is the common difference, $n$ is the number of terms and $S_n$ is the sum of the terms.

Let’s see how this formula came to be.

Let $a, a+d, a+2d, a+3d, …., a+(n-1)d$ be an AP, where $a$ is the first term, $d$ is the common difference, and $n$ is the number of terms.

Now, the sum = $S_n = a + a + d + a + 2d + a + 3d + …. + a + (n-1)d$

Also we can write in reverse, $S_n = a + (n-1)d + a + (n-2)d + ….. + a + d + a$

Now, adding these two we get,

$2S_n = [a + a + (n-1)d] + [a + d + a + (n-2)d] + …… + [a + (n-1)d + a]$

⇒ $2S_n = [2a + (n-1)d] + [2a + (n-1)d] + …… + [2a + (n-1)d]$

⇒ $2S_n = n[2a + (n-1)d]$

⇒ $S_n = \frac{n}{2}[2a + (n-1)d]$

Therefore, the formula of the sum of AP is $S_n = \frac{n}{2}[2a + (n-1)d]$.

The sum of AP when the last term is given:

When the last term of the AP is given we can calculate the sum of the terms of an AP by using the formula:

$S_n = \frac{n}{2}(a + l)$, where $a$ is the first term, $l$ is the last term, $n$ is the number of terms and $S_n$ is the sum of the terms.

Again let’s see how this formula came to be.

We know the sum of the terms of an AP,

$S_n = \frac{n}{2}[2a + (n-1)d]$

⇒ $S_n = \frac{n}{2}[a + a + (n-1)d]$ …………. (1)

We also know the formula of the last term $l = a + (n-1)d$

Putting this value in the equation (1) we get,

⇒ $S_n = \frac{n}{2}[a + l]$

Therefore, the formula of the sum of the terms of an AP, when the last term is given is,

$S_n = \frac{n}{2}[a + l]$

Arithmetic Mean (AM)

The arithmetic mean (AM), often referred to simply as the mean or average, is a measure of central tendency that is commonly used in statistics and mathematics. It indicates the central value of a set of numbers. The arithmetic mean of a set of $n$ numbers is calculated by summing all the numbers and then dividing by $n$.

For example, AM of 2, 4, 6, 8, 10 is $\frac{2 + 4 + 6 + 8 + 10}{5} = 6$.

Important Properties of an AP

1. If a fixed number is added to or subtracted from each term of a given A.P., then the resulting series is also an A.P. and its common difference remains the same.

2. If each term of an A.P. is multiplied by a fixed constant or divided by a non-zero fixed constant then the resulting series is also in A.P.

3. If $a_1, a_2, a_3 \ldots$ and $b_1, b_2, b_3 \ldots$ are two A.P’s, then $a_1 \pm b_1, a_2 \pm b_2, a_3 \pm b_3 \ldots$ are also in A.P.

4. If terms of an A.P. are taken at equal intervals, then the new sequence formed as also an A.P.

Eg, If from A.P., 1, 3, 5, 7, 9, 11, 13,.... we take terms at equal intervals, let's say first, third, fifth, seventh,....terms, then the resultant sequence will be

1, 5, 9, 13, ....which is also an A.P.

5. If $a_1, a_2, a_3, \ldots, a_n$ are in A.P., then $
a_r=\frac{a_{r-k}+a_{r+k}}{2}, \forall k, 0 \leq k \leq n-r
$

6. Choosing terms in A.P.

If some of a few terms (like 3, 4, or 5 terms) in an A.P. is given in the problem, then selecting the following terms reduces the calculation
- If we need to choose three terms in an A.P., then choose $(a-d), a,(a+d)$
[Note: Here the first term is $a-d$, and the common difference is $d$]
- If we need to choose four terms in an A.P., then choose $(a-3 d),(a-d),(a+d),(a+3 d)$
[Note: Here first term is $a-3d$, and the common difference is $2d$]
- If we need to choose five terms in an A.P., then choose $(a-2 d),(a-d), a,(a+d)$, $(\mathrm{a}+2 \mathrm{~d})$
[Note: Here the first term is $a-2d$, and the common difference is $d$]

7. The sum of terms equidistant from the beginning and end of an AP is constant and it equals the sum of the first and the last terms.

$a_1+a_n=a_2+a_{n-1}=a_3+a_{n-2}=\ldots \ldots=a_r+a_{n-r+1}$

8. If $a, b, c$ are in A.P., then $2 b=a+c$

Tips and Tricks

• If we are given a sequence and need to check if it's an AP, then check if the difference between consecutive terms is constant or not.

• For a quick calculation of the sum of the terms of an AP, use the formula

$S_n=\frac{n}{2}(a + l)$, if the last term is known.

• To find the number of terms of an AP use the formula:

$n=\frac{l-a}{d}+1$

• For solving three unknown terms in an AP whose sum or product is given, then the terms should be assumed as $a-d, a$, and $a+d$.

• For solving four unknown terms in an AP whose sum or product is given, then the terms should be assumed as $a-3d, a-d, a+d$, and $a+3d$.

• If the $n$th term of a sequence is a linear expression in $n$, i.e. $t_n = Cn + D$, then C is always the common difference.

• The sum of $n$ natural numbers is $\frac{n(n+1)}{2}$.

• The sum of the square of $n$ natural numbers $\frac{n(n+1)(2n+1)}{6}$.

• The sum of the cube of $n$ natural numbers $[\frac{n(n+1)}{2}]^2$.

Recommended Video on Arithmetic Progression

Solved Examples Based on Arithmetic Progression

Example 1. The sum of 10 terms of the arithmetic series is 390. If the third term of the series is 19, find the first term.

Solution:

Given: The sum of 10 terms of the arithmetic series is 390.

So, $n=10$

The third term of the series is 19.

Let the first term of the series be $a$.

We know, sum of arithmetic progression (A.P.) = $\frac{n}{2}[2a+(n-1)d]$

$n^{th}$ term = $a+(n-1)d$

So, $3^{rd}$ term ⇒ $a+(3-1)d=19$

⇒ $a+2d=19$ ----------------------------(1)

Sum of 10 terms = $\frac{10}{2}[2a+(10-1)d] =390$

⇒ $2a+9d=78$ ---------(2)

Multiplying 9 with equation (1) and 2 with equation (2), we get,

⇒ $9a+18d=171$ ------------------------(3)

⇒ $4a+18d=156$ ------------------------(4)

Subtracting (4) from (3), we get,

$5a=15$

$\therefore a=3$

Hence, the required answer is 3.

Example 2: What is the sum of the first 9 terms of an arithmetic progression, if the first term is 7 and the last term is 55?

Solution:

Given: The first term is 7 and the last term is 55.

Using the formula, S9 = $\frac{n}{2}(a+l)$

Where $a$ is the first term, $l$ is the last term of the A.P., and n is the number of terms.

By putting the value of 1st and last term,

⇒ S9 = $\frac{9}{2}$(7 + 55)

⇒ S9 = $\frac{9}{2}$ × 62

$\therefore$ S9 = 9 × 31 = 279

Hence, the required answer is 279.

Example 3: If $P=2^2+6^2+10^2+14^2+....+ 94^2$ and $Q=1^2+5^2+9^2+...+81^2$, then what is the value of $P - Q$?

Solution:

Given: $P=2^2+6^2+10^2+14^2+....+94^2$ and $Q=1^2+5^2+9^2+...+81^2$

$⇒P-Q = (2^{2}-1^{2})+(6^{2}-5^{2})+(10^{2}-9^{2})+....+(82^{2}-81^{2})+86^{2}+90^{2}+94^{2}$

$⇒P-Q=3+11+19+27+.......+163(\text{A.P. with 21 terms})+86^{2}+90^{2}+94^{2}$

$⇒P-Q=\frac{21}{2}[2×3+(21–1)8]+86^{2}+90^{2}+94^{2}$

$⇒P-Q=\frac{21}{2}[6+(20)8]+86^{2}+90^{2}+94^{2}$

$⇒P-Q=\frac{21}{2}[166]+(90-4)^{2}+90^{2}+(90+4)^{2}$

$⇒P-Q=1743+(90^{2}-2×90×4+4^{2})+90^{2}+(90^{2}+4^{2}+2×90×4)$

$⇒P-Q=1743+8100+16+8100+8100+16$

$\therefore P-Q=26075$

Hence, the required answer is 26075.

Example 4: Three numbers are in Arithmetic Progression (A.P.) whose sum is 30 and the product is 910. Then the greatest number in the AP is

Solution:

Let three numbers in A.P. be a – d, a, and a + d, respectively.

According to the question, a – d + a + a + d = 30

⇒ 3a = 30

⇒ a = $\frac{30}{3}$ = 10

Again, a×(a – d)×(a + d) = 910

⇒ 10×(10 – d)×(10 + d) = 910

⇒ 100 – d2 = 91

⇒ d2 = 100 – 91 = 9

⇒ d = $\sqrt{9}$ = 3

$\therefore$ Largest number = a + d = 10 + 3 = 13

Hence, the required answer is 13.

Example 5: The first term of an arithmetic progression is 22 and the last term is –11. If the sum is 66, the number of terms in the sequence is

Solution:

Let the first term as $a$, the last term as $l$, and the number of terms as $n$.

Given: $a$ = 22, $l$ = –11

The sum of an arithmetic progression is given by

$S = \frac{n}{2}(a + l)$

⇒ 66 = $\frac{n}{2}$(22 – 11)

$\therefore n$ = 12

Hence, the correct answer is option (2).

Example 6: The $8^{\text {th }}$ common term of the series $
\begin{aligned}
& \mathrm{S}_1=3+7+11+15+19+\cdots \\
& \mathrm{S}_2=1+6+11+16+21+\cdots
\end{aligned}
$
is $\qquad$

[JEE MAINS 2023]

Solution

$8^{\text {th }}$ common term of the series
$
\begin{aligned}
& \mathrm{S}_1=3+7+11+15+19+\ldots \ldots \\
& \mathrm{S}_2=1+6+11+16+21+\ldots \ldots
\end{aligned}
$

First common term $=11$
common diff of the AP of common terms
$
\begin{aligned}
& =\mathrm{L} . \mathrm{C} . \mathrm{M} \text { of }\{4,5\} \\
& =20
\end{aligned}
$
$
\begin{aligned}
& \therefore \mathrm{AP} \\
& 11,31,51, \quad \ldots \ldots \\
& \mathrm{T}_8=11+(8-1) 20 \\
& =11+140 \\
& \mathrm{~T}_8=151
\end{aligned}
$

Hence, the answer is (151).

Example 7: Let $a, b, c>1, a^3, b^3$ and $c^3$ be in A.P., and $\log _a b, \log _c$ a and $\log _b c$ be in G.P. If the sum of first 20 terms of an A.P., whose first term is $\frac{a+4 b+c}{3}$ and the common difference is $\frac{a-8 b+c}{10}$ is -444, then abc is equal to:
[JEE MAINS 2023]

Solution
$
\begin{aligned}
& \text { If } \log _{\mathrm{a}} \mathrm{b}, \log _{\mathrm{c}} a, \log _b c \rightarrow \text { G.P. } \\
& \left(\log _c a\right)^2=\log _a b \times \log _b c \\
& \left(\log _{\mathrm{c}} \mathrm{a}\right)^2=\log _{\mathrm{a}} \mathrm{c} \\
& \Rightarrow\left(\log _c a\right)^2=\frac{1}{\log _c a} \\
& \Rightarrow\left(\log _{\mathrm{c}} \mathrm{a}\right)^3=1 \\
& \Rightarrow \log _{\mathrm{c}} \mathrm{a}=1 \\
& \mathrm{a}=\mathrm{c} \\
& \text { If } a^3 b^3 c^3 \rightarrow \mathrm{A} . \mathrm{P} \\
& 2 b^3=a^3+c^3 \\
& \text { If } \mathrm{a}=\mathrm{c} \\
& \Rightarrow \mathrm{a}=\mathrm{b}=\mathrm{c} \\
\end{aligned}
$

For AP
$
\begin{aligned}
& A=\frac{a+4 a+a}{3} \quad D=\frac{a-8 a+a}{10} \\
& \mathrm{~A}=2 \mathrm{a} \quad \mathrm{D}=\frac{-3 \mathrm{a}}{5} \\
& S_{20}=\frac{20}{2}\left[2 \times 2 a+(20-1)\left(\frac{-3 a}{5}\right)\right] \\
& =10\left[4 a-\frac{57 a}{5}\right] \\
& =10\left[-\frac{37 a}{5}\right]=-444 \\
& \Rightarrow \mathrm{a}=\frac{444 \times 5}{37 \times 10} \\
& a=6 \\
& \Rightarrow \mathrm{abc}=6 \times 6 \times 6=216 \\
&
\end{aligned}
$

Example 8: If $a_1, a_2, a_3 \ldots \ldots$ and $b_1, b_2, b_3 \ldots \ldots$ are A.P., and $a_1=2, a_{10}=3, a_1 b_1=1=a_{10} b_{10}$ then $a_4 b_4$ is equal to
[JEE MAINS 2023]

Solution
$
\begin{aligned}
& \mathrm{a}_1=2, \quad \mathrm{a}_{10}=2+(10-1) \mathrm{d}=3 \Rightarrow \mathrm{d}=\frac{1}{9} \\
& \mathrm{a}_4=2+(4-1) \times \frac{1}{9}=\frac{7}{3} \\
& \mathrm{a}_1 \mathrm{~b}_1=1 \Rightarrow \mathrm{b}_1=\frac{1}{2}, \quad \mathrm{a}_{10} \mathrm{~b}_{10}=1 \Rightarrow \mathrm{b}_{10}=\frac{1}{3} \\
& \mathrm{~b}_{10}=\frac{1}{2}+(10-1) \times \mathrm{d}=\frac{1}{3} \Rightarrow 9 \mathrm{~d}=-\frac{1}{6} \Rightarrow \mathrm{d}=-\frac{1}{5^4} \\
& \mathrm{~b}_4=\frac{1}{2}+(4-1) \times\left(-\frac{1}{54}\right)=\frac{1}{2}-\frac{1}{18}=\frac{4}{9} \\
& \mathrm{a}_4 \mathrm{~b}_4=\frac{7}{3} \times \frac{4}{9}=\frac{28}{27}
\end{aligned}
$

Example 9: If the 10th term of an A.P. is $\frac{1}{20}$ and its 20th term is $\frac{1}{10}$, then the sum of its first 200 terms is
[JEE MAINS 2023]

Solution
$
\begin{aligned}
& a_{10}=a+9 d=1 / 20 \\
& a_{20}=a+19 d=1 / 10
\end{aligned}
$

On subtracting them, we get $d=1 / 200$
$
\begin{aligned}
& a+9 / 10=1 / 20 \Rightarrow a=1 / 200 \\
& S_{200}=\frac{200}{2}[2 / 200+(199) \times 1 / 200]=\frac{201}{2}
\end{aligned}
$

Example 10: Let $f: R \rightarrow R$ be such that for all $x \in R\left(2^{1+x}+2^{1-x}\right), f(x)$ and $\left(3^x+3^{-x}\right)$ are in A.P., then the minimum value of $f(x)$ is:
[JEE MAINS 2023]

Solution
If $a, b, c$ are in $A P$, then $2 b=a+c$
$
2 f(x)=\left(2 \frac{1}{2^x}+2.2^x\right)+\left(3^x+\frac{1}{3^x}\right)
$

Now, $A M \geq G M$
$
\begin{aligned}
& \frac{a+b}{2} \geq \sqrt{a b} \\
& \frac{3^x+\frac{1}{3^x}}{2} \geq \sqrt{1} \\
& \left(3^x+\frac{1}{3^x}\right) \geqslant 2
\end{aligned}
$

Value equals 2 at $3^x=\frac{1}{3^x} \Rightarrow x=0$
Similarly, $\frac{1}{2^x}+2^x \geq 2$, and this holds at $x=0$
So, $2($ minimum of $f(x))=2(2)+(2)$ $\min f(x)=3$

Summary

Arithmetic Progression is a sequence in which there is a constant increase or decrease between successive terms. It is used to generalize the pattern we see in day-to-day life. Its direct formula to find the number of terms, the sum of terms, and most importantly, the nth term makes it suitable for use in many fields. Arithmetic progressions are essential in mathematics for their ability to model and predict sequential patterns with precision and efficiency.