Classification of numbers
Numbers are an integral part of our daily lives and serve many purposes. Classification of numbers in maths is also very important. Numbers are fundamental tools for counting dates and times, managing finances, and quantifying items like groceries. Whether it's tallying the days in a month, calculating expenses, or counting fruits, numbers are indispensable.
CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts
XAT 2025: Section-wise Preparation Tips | Sample Paper
Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers
- Types of numbers and their classifications
- Prime and Composite Numbers
- Even and Odd Numbers
- Practice Questions on the classification of numbers

We utilize numbers in various arithmetic operations, including addition, subtraction, multiplication, and division, to solve everyday problems and make informed decisions. Just as we categorize essential items like vegetables, fruits, or vehicles based on their types and uses, numbers can also be classified into distinct categories, each with unique properties and applications.
After we learn the classification of numbers with examples, we can better appreciate their roles and leverage their properties in basic and complex scenarios.
In this article, we will learn how to classify real numbers, how to classify numbers rational & irrational, classification of fraction, whole numbers, imaginary numbers, complex numbers and many more.
Types of numbers and their classifications
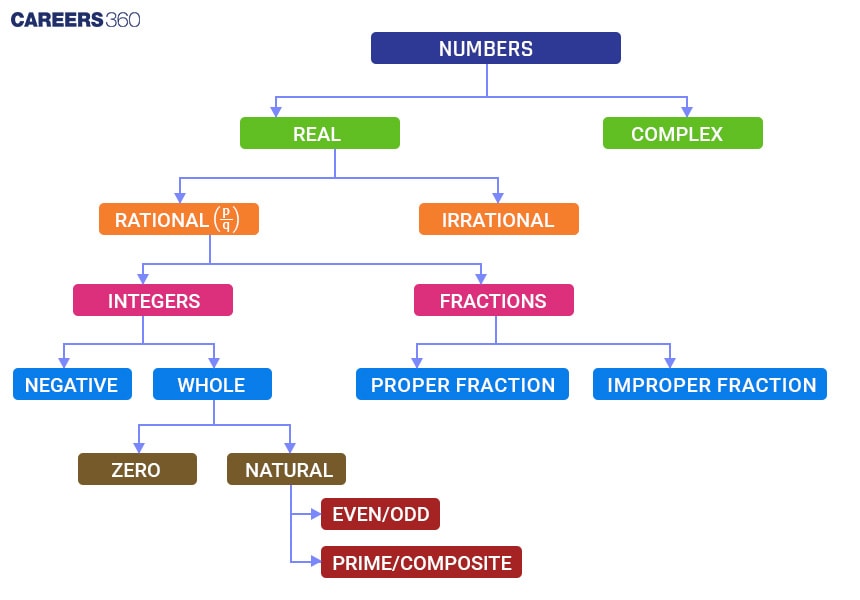
Classification of numbers can be visually represented on a number line, a straight line where each point corresponds to a number. The numbers that are placed on the right side of zero are called positive numbers, while negative numbers are placed on the left side of zero.
Real numbers
Numbers that can be placed on the number line, positive or negative, are called real numbers.
Real numbers are used to solve various problems in our day-to-day lives.
Real numbers can be further classified as
Rational numbers
Irrational numbers
Example:- $1, -1, \pi = 3.14159….,-\frac{1}{2}, \sqrt{3}$
Rational Numbers
A number is called a rational number if it can be expressed as a fraction where the numerator and denominator are integers, and the denominator is not zero.
It is written like $\frac{p}{q}$, where p and q are integers and $q \neq 0$
Rational numbers can be negative or positive.
The sum or product of two rational numbers is rational.
Example: $\frac12,-\frac32,\frac43$, etc.
Irrational Numbers
If a number can not be written as a fraction or ratio, then it is called an Irrational number.
Irrational numbers can be negative or positive.
The sum or product of two irrational numbers is sometimes irrational.
Example: $\pi, \sqrt{3}, \sqrt{\frac{8}{25}},\sqrt{17}$, etc.
Integers

Integers are numbers that have no fractional parts or decimals. It can be negative, positive, or zero.
We can use integers for arithmetic operations like addition, subtraction, multiplication, and division.
All whole numbers are integers.
Example: 0, 7, 9, -3, -55, etc.
Properties of Integers:
Some properties of integers are written below.
Commutative property: Order does not matter if we add or multiply two integers.
- Example: a + b = b + a, where a and b are integers
Closure property: The sum or product of any two integers is always an integer.
- Example: 5 × 6 = 30, which is an integer
Associative property: When we add or multiply three or more integers, how the numbers are grouped does not change the result.
- Example: a + (b + c) = (a + b) + c, where a, b, and c are integers
Distributive Property: Multiplying a sum of two integers by a third integer gives the same result as multiplying each integer separately by the third integer and then adding the products.
- Example: a × (b + c) = (a × b) + (a × c), where a, b, and c are integers
Zero property: If we multiply any integer with zero, the result will be zero.
- Example: 0 × a = 0, where a is an integer
Identity property: If we multiply any integer with 1, we will get the same number back.
- Example: 1 × a = a, where a is an integer
Fractions
Fractions are numbers that can be written as a ratio or $\frac{p}{q}$ form, $q \neq 0$, and not a whole number.
We can say that every rational number is a fraction. But not every fraction is a rational number.
Because Fractions can be negative.
Example: $\frac{1}{2}, -\frac{3}{2},-\frac{5}{7},$ etc.
Mainly fractions are of 3 types:
Proper fractions: Here, the numerator will be smaller than the denominator.
Example- $\frac{1}{2},\frac{5}{6},\frac{9}{10},$ etc.Improper fractions: Here, the numerator will be greater than the denominator.
Example- $\frac{3}{2},\frac{7}{6},\frac{11}{10},$ etc.
Whole Numbers
Numbers starting from 0 to infinity are called Whole Numbers. So, we can say that including 0, every natural number is a whole number. Whole numbers do not consist of fractions, decimals, or negative numbers.
Example: 0, 10, 11, 20, etc.
Properties of whole numbers:
Some properties of whole numbers are written below.
Commutative property: Order does not matter if we add or multiply two whole numbers.
Example: a + b = b + a, where a and b are whole numbers
Closure property: The sum or product of any two whole numbers is always a whole number.
Example: 5 × 6 = 30, which is a whole number
Associative property: When we add or multiply three or more whole numbers, how the numbers are grouped does not change the result.
Example: a + (b + c) = (a + b) + c, where a, b, and c are whole numbers
Distributive Property: Multiplying a sum of two whole numbers by a third whole number gives the same result as multiplying each whole number separately by the third whole number and then adding the products.
Example: a × (b + c) = (a × b) + (a × c), where a, b, and c are whole numbers
Zero property: If we multiply any whole number with zero, the result will be zero.
Example: 0 × a = 0, where a is a whole number
Identity property: If we multiply any whole number by 1, we will get the same number back.
Example: 1 × a = a, where a is a whole number
Natural Numbers
Numbers starting from 1 to infinity are called natural numbers. These numbers are used for counting purposes and are always positive, greater than zero.
0 is not considered a natural number.
Example: 1, 2, 3, 10, etc.
Properties of natural numbers:
Some properties of natural numbers are written below.
Commutative property: Order does not matter if we add or multiply two natural numbers.
Example: a + b = b + a, where a and b are natural numbers
Closure property: The sum or product of two natural numbers or integers is always a natural number.
Example: 5 × 6 = 30, which is a natural number
Associative property: When we add or multiply three or more natural numbers, how the numbers are grouped does not change the result.
Example: a + (b + c) = (a + b) + c, where a, b, and c are natural numbers
Distributive Property: Multiplying a sum of two natural numbers by a third natural number gives the same result as multiplying each natural number separately by the third natural number and then adding the products.
Example: a × (b + c) = (a × b) + (a × c), where a, b, and c are natural numbers
Zero property: If we multiply any natural number with zero, the result will be zero.
Example: 0 × a = 0, where a is a natural number
Identity property: If we multiply any natural number by 1, we will get the same number back.
Example: 1 × a = a, where a is a natural number
Imaginary Numbers
As the name suggests, Imaginary numbers are not real numbers. If we square a number and get a negative result, then that number is called an Imaginary number.
We define imaginary numbers as i and the value of i2 = -1
Example: Suppose 2i is an imaginary number. Because if we square the number, we will get 4i2, which is equal to -4 as the value of i2 is -1.
Some more examples of imaginary numbers are $\sqrt{-2}, 3 + \sqrt{-25}, \sqrt{-36}$, etc.
Complex Numbers

Complex numbers are those non-real numbers that are made by combining real numbers and imaginary numbers.
It can be written as (a + ib), where a and b are real numbers and i is the imaginary number
As we know the value of i2 = -1, so i = $\sqrt{-1}$
Example: $3+6i=3+6 \sqrt{-1}$
The Conjugate of a complex number a + ib is a - ib, where a is the real part, and ib is the imaginary part.
The modulus of a complex number a + ib is given by $\left | a+ib \right |$ which is equal to $\sqrt{a^2 +b^2}$.
Two complex numbers a + ib and c + id can be called equal if a = c and b = d.
The sum of two complex numbers a + ib and c + id is (a + c) + i(b + d).
Similarly, the subtraction of two complex numbers a + ib and c + id is (a - c) + i(b - d).
The product of two complex numbers a + ib and c + id is (ac - bd) + i(ad + bc) as i2 = -1.
Division of two complex numbers a + ib and c + id = $\frac{\left | a+ib \right |}{\left | c+id \right |}=\frac{\left | a+ib \right |\left | c-id \right |}{\left | c+id \right |\left | c-id \right |}=\frac{(ac+bd)+i(bc-ad)}{c^2+d^2}$
Prime and Composite Numbers
A natural number greater than 1 that has no positive divisors other than 1 and itself is called a Prime number. So, we can say that if a number cannot be formed by multiplying two smaller natural numbers, it can be called a Prime number.
Example: 7 is a prime number because it has no divisors other than 1 and itself.
Other examples of odd numbers are 3, 5, 11, 47, etc.
If a natural number greater than 1 has more than two positive divisors is called a Composite number.
Example: 10 is a composite number because it has divisors other than 1 and itself, specifically 2 and 5.
Other examples of composite numbers are 15, 20, 22, 25, etc.
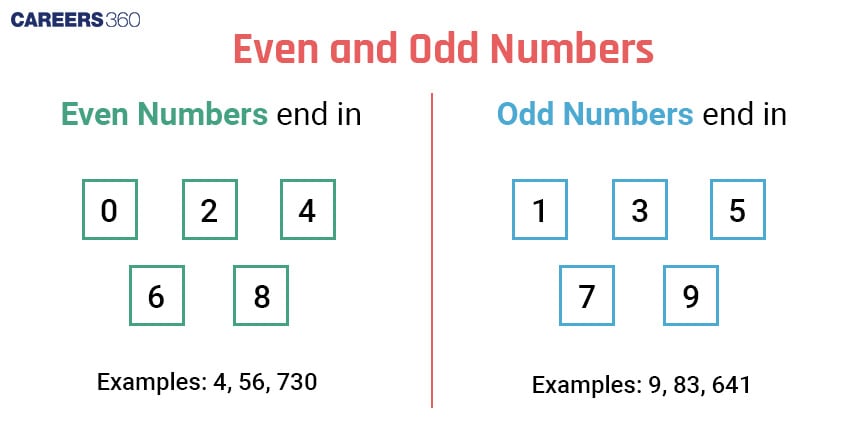
Even and Odd Numbers
If we divide a number by 2 and get no remainder, then that number is called an Even number.
Even numbers can be negative or positive. But the even numbers can not be decimals or fractions.
Example: 12, 16, 18, -28, -50, etc.
If we divide a number by 2 and there is a remainder equal to 1, then that number is called an Odd number.
Odd numbers are in the form of 2k + 1, where k is an integer
Like even numbers, Odd numbers can be negative or positive but can not be decimals or fractions.
Example: 1, 7, 11, -3, -51, etc.
Practice Questions on the classification of numbers
Q1. Use the distributive property to get the value: 24 × 48 + 24 × 50
Answer: Using distributive property, we get,
24 × (48 + 50)
= 24 × 98
= 2352
Hence, the correct answer is 2352.
Q2. Add the given numbers using the associative property: 87 + 113 + 387
Answer: Using associative property, we get,
87 + (113 + 387)
= 87 + 500
= 587
Hence, the correct answer is 587.
Q3. Which is the smallest whole number?
2
B. 1
C. 3
D. 0
Answer: Zero is the smallest whole number.
Hence, the correct answer is option (D).
Q4. Which number is an even number as well as a prime number?
4
2
1
6
Answer: 2 is an even number as well as a prime number.
Hence, the correct answer is option (B).
Q5. Which of the following statements is true?
0 is an odd number.
0 is an even number.
Both statements are true.
None of the above.
Answer: 0 is not an odd number.
If we divide 0 by 2, then we get 0. So no remainder.
Therefore, 0 is an even number.
Hence, the correct answer is option (B).
Q6. Determine if 0.25 is a rational number.
Answer: We can write 0.25 as $\frac{25}{100}=\frac{1}{4}$, which is a fraction.
Hence, 0.25 is a rational number.
Q7. Choose which one is not an irrational number.
$\sqrt{15}$
$\sqrt{36}$
$\sqrt{5}$
$\sqrt{50}$
Answer: Here $\sqrt{36}=6$ which can be written as $\frac{6}{1}$.
So, it is a rational number. The rest of the options can not be written in a fraction form.
So, those are irrational numbers.
Hence, the correct answer is option (B).
Q8. If a = 10 and b = 4, then the value of a × b is even or odd.
Answer: a × b = 10 × 4 = 40, which is an even number,
because if we divide 40 by 2, there is no remainder. Hence, the correct answer is “even”.
Q9. Determine whether 1 is a prime number or a composite number.
Answer: The definition of a prime number says a prime number should only have two divisors, 1 and itself. Also, the definition of a composite number says a composite number should have at least 1 divisor other than 1 and itself.
However, 1 is neither a prime nor a composite number since it has exactly one factor.
Q10. If we subtract 199 from 217, is the result prime or composite?
Answer: 217 - 199 = 18, which is a composite number, as it has divisors 2, 3, and 6, other than 1 and itself. So, 18 has more than 2 factors and hence, it is a composite number. Hence, the correct answer is “Composite”.
Q11. If a = 5 + 8i and b = 3 – i, then find $\frac{a}{b}$.
A. $\frac{23+19i}{10}$
B. $\frac{19+19i}{10}$
C. $\frac{23+19i}{11}$
D. $\frac{23+29i}{10}$
Answer:
We know, $i^2=-1$
Given: a = 5 + 8i and b = 3 – i
$\frac{a}{b}=\frac{5+8i}{3-i}=\frac{(5+8i)(3-i)}{(3-i)(3-i)}=\frac{15+24i-5i-8i^2}{9-i^2}=\frac{23+19i}{10}$
Hence, the correct answer is $\frac{23+19i}{10}$.
Q12. Find the conjugate of x – y if x = 10 + 3i and y = 3 + 2i.
Answer: x – y = 10 + 3i – 3 – 2i = 7 + i
As we know, the conjugate of a complex number a + ib is a - ib.
So, the conjugate of 7 + i is 7 – i.
Hence, the correct answer is 7 – i.
Q13. What is the sum of the following fractions?
$\frac{3}{5},\frac{7}{15},\frac{6}{45}$
A. $\frac{6}{5}$
B. $\frac{5}{6}$
C. $\frac{3}{2}$
D. $\frac{2}{3}$
Answer:
$\frac{3}{5}+\frac{7}{15}+\frac{6}{45}=\frac{27+21+6}{45}=\frac{54}{45}=\frac{6}{5}$
Hence, the correct answer is $\frac{6}{5}$.
Q14. Kushal has a budget of Rs. 200 and wants to buy pens that cost Rs. 3 each and notebooks that cost Rs. 7 each. What are the number of sets of pens and notebooks Kushal can buy within his budget?
A. 20
B. 15
C. 25
D. 10
Answer:
The cost of 1 set of pens and notebooks = Rs. 3 + Rs. 7 = Rs. 10
Therefore in Rs. 200, Kushal can buy $\frac{200}{10}=20$ sets of pens and notebooks.
Hence, the correct answer is 20.
Q15. Simplify the expression $\sqrt3(\sqrt{16}+\sqrt{25})$. Is the result rational or irrational?
Answer:
$\sqrt3(\sqrt{16}+\sqrt{25})=\sqrt{48}+\sqrt{75}=4\sqrt3+5\sqrt3=9\sqrt3$
$9\sqrt3$ is an irrational number.
Hence, the result will be an irrational number.