Compound Interest: Definition, Formula, Question, Examples, Calculator

Compound interest is an important concept in the field of finance and Mathematics. Unlike simple interest, in compound interest, we add the interest after each year or each term and then get the compound interest for the next term or year with that total amount as principal.

To solve compound interest problems, we can use resources like compound interest problems with solutions PDF for practice.

For ease, we can use a compound interest formula calculator or even the compound interest formula in Excel. Additionally, tools like a compound interest calculator in India or a compound interest calculator online are available. For investors in India, a compound interest calculator India SIP can help manage systematic investment plans effectively.

What is Compound Interest?

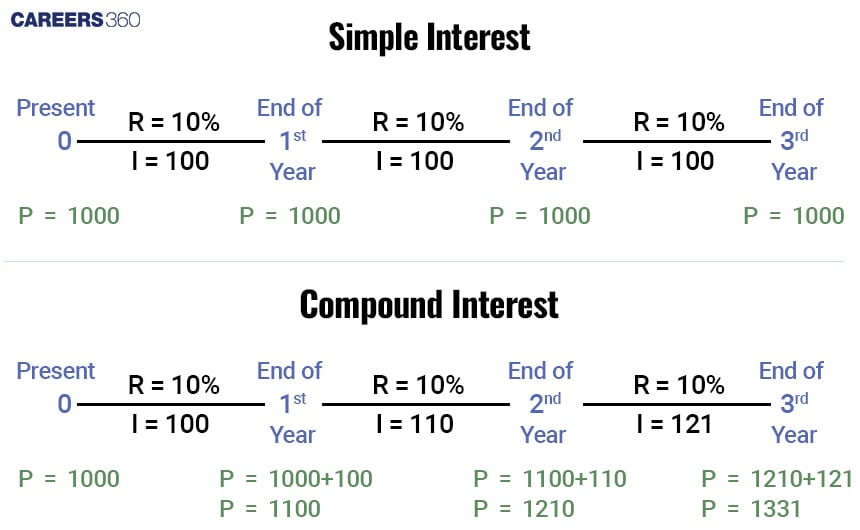
Compound interest is a type of interest that is calculated not only by the initial principal but also by the accumulated compound interest from the initial principal. For 2nd term or 2nd year, we use (Initial principal + Compound interest interest for 1st year or 1st term) as the principal.

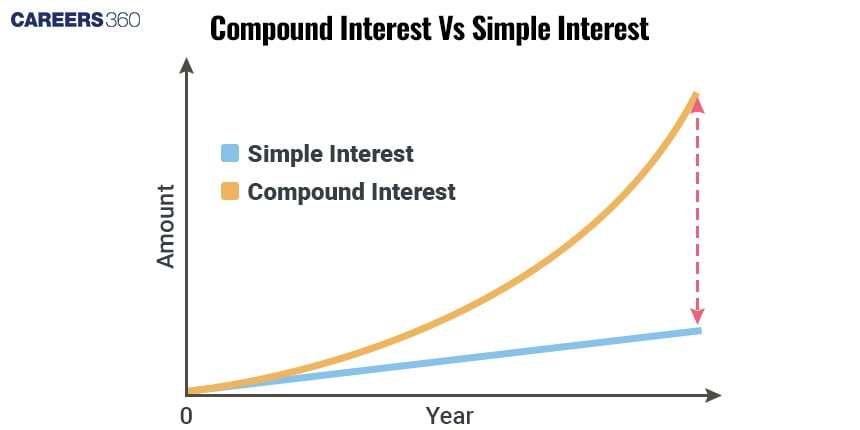
Unlike simple interest, which is calculated only on the principal amount, compound interest allows interest to be earned on the interest itself, leading to exponential growth over time.

For the same amount of money for the same rate of interest, compound interest is equal to the simple interest for the 1 year if compounded annually.

Example:

How to calculate Compound Interest using Simple Interest?

We can also calculate the compound interest using Simple interest. When compounded annually, compound interest is the same as simple interest for 1 year for the same principal and rate of interest.

So, we will calculate the simple interest for 1 year with the initial principal. Then for 2nd year, the principal will be (Initial principal + Simple interest for 1st year).

We will again calculate the simple interest for 1 year with the new principal.

Then for the 3rd year, again we will add the simple interest for this year with the principal for 2nd year.

This process goes on in the same way.

Calculating compound interest using simple interest is a very lengthy process after 2nd year. This is why we use the compound interest formula to calculate easily and save time.

Example:

Find the compound interest on Rs. 2000 for 2 years at an annual interest rate of 5%.

We know that compound interest is equal to the simple interest for the 1 year if compounded annually.

So, simple interest for 1 year = $\frac{2000 × 2 × 5}{100}$ = 200

Amount after 1 year = 2000 + 200

Simple interest for next year with principal 2200,

= $\frac{2200 × 2 × 5}{100}$ = 220

So, total amount will be 2200 + 220 = 2420 after 2 years

So, compound interest = 2420 - 2000 = 420

The general formula to calculate Compound Interest

The general formula for compound interest is:

$\text{Compound Interest}=\text{Principal}×(1+\frac{\text{Rate}}{100})^{\text{Time}}-\text{Principal}$

But generally, we calculate the total amount first.

Then, Compound interest = Total amount - Principal

In notation, we can write this formula:

When compounded annually, $ A= P(1+\frac{R}{100})^{T}$,

Where A is the total amount after T years,

P is the principal amount,

R is the rate of interest per annum,

and T is the time in years.

Derivation of the Compound Interest formula

We can derive the compound interest formula using the formula of simple interest, as we know if compounded annually, then for 1-year simple interest and compound interest are the same for the same rate of interest and principal.

Let P is the principal amount,

R is the rate of interest per annum,

and T is the time in years

So, simple interest for 1 year, SI1 = $\frac{PTR}{100}$

Compound interest will be also the same for 1 year.

Total amount after the first year = P + SI1 = $P+\frac{PTR}{100}=P(1+\frac{R}{100})$ [$\because$ T = 1]

Let P2 = $P(1+\frac{R}{100})$

For 2nd year, simple interest, SI2 = $\frac{P_2TR}{100}=\frac{P_2R}{100}$ [$\because$ T = 1]

Total amount after the 2nd year, P2 + SI2 = P2 + $\frac{P_2R}{100}=P_2(1+\frac{R}{100})$

Putting the value of P2, we get,

Total amount after the 2nd year, P2 + SI2 = $P(1+\frac{R}{100})(1+\frac{R}{100})=P(1+\frac{R}{100})^2$

Similarly, total amount after n year = $P(1+\frac{R}{100})^n$

Compound interest after n year = Total amount after n year - Principal

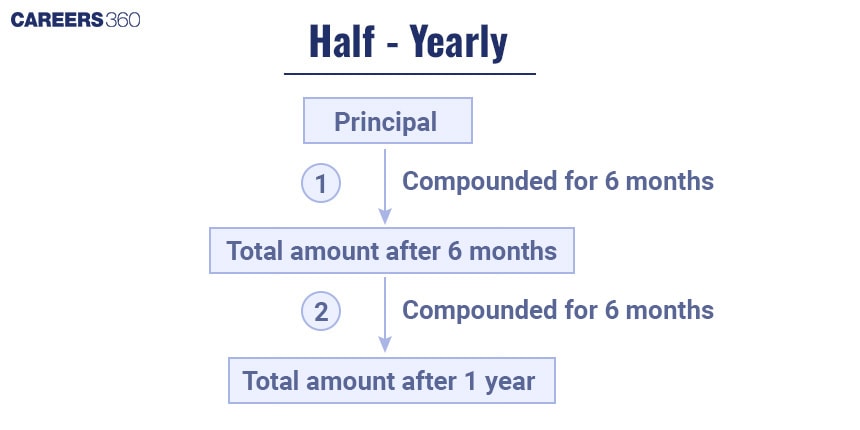
How to Calculate Compound Interest if interest is compounded/reckoned half-yearly?

When compounded half-yearly, interest is compounded twice a year. So in the formula, the terms will be 2. Also, the rate of interest will be half, as it compounded 2 times in a year.

When compounded half-yearly, $ A= P(1+\frac{\frac{R}{2}}{100})^{nT}$,

Where A is the total amount,

P is the principal amount,

R is the rate of interest per annum, [Here Rate will be $\frac{R}{2}$]

N = Number of terms rate is compounded [Here N will be 2]

and T is the time in years.

So, final formula when compounded half-yearly is $ A= P(1+\frac{\frac{R}{2}}{100})^{2T}$

How to Calculate Compound Interest if interest is compounded/reckoned quarterly?

When compounded quarterly, interest is compounded 4 times in a year. So in the formula, the terms will be 4. Also, the rate of interest will be divided by 4, as it is compounded 4 times in a year.

When compounded quarterly, $ A= P(1+\frac{\frac{R}{4}}{100})^{nT}$,

Where A is the total amount,

P is the principal amount,

R is the rate of interest per annum, [Here Rate will be $\frac{R}{4}$]

N = Number of terms rate is compounded [Here N will be 4]

and T is the time in years.

So, final formula when compounded quarterly is $ A= P(1+\frac{\frac{R}{4}}{100})^{4T}$

How to Calculate Compound Interest if interest is compounded/reckoned monthly?

When compounded monthly, interest is compounded 12 times in a year. So in the formula, the terms will be 12. Also, the rate of interest will be divided by 12, as it is compounded 12 times in a year.

When compounded monthly, $ A= P(1+\frac{\frac{R}{12}}{100})^{nT}$,

Where A is the total amount,

P is the principal amount,

R is the rate of interest per annum, [Here Rate will be $\frac{R}{12}$]

N = Number of terms rate is compounded, [Here N will be 12]

and T is the time in years.

So, final formula when compounded monthly is $ A= P(1+\frac{\frac{R}{12}}{100})^{12T}$

Application of Compound interest to calculate depreciation:

In some cases where the value of some articles, cars, bikes, furniture, buildings, etc., decreases, we can use the compound interest formula to calculate the value.

The formula will be:

Dvalue after n years = $P (1-\frac{r}{100})^{nt}$,

Where P is the initial value,

R is the rate of interest per annum,

N =Number of compounding cycles in one year,

and T is the time in years.

Example:

The price of the table depreciates every year by 20%. If the value of the table after 2 years will be Rs. 32,000, then what is the present price (in Rs.) of the table?

Solution: Let the present value be $x$.

Value after 2 years = $x × (1-\frac{R}{100})^2$, where $R$ is the rate.

$32000 = x × (1-\frac{20}{100})^2$

⇒ $32000 = x × (\frac{4}{5})^2$

⇒ $32000 = x × (0.8)^2$

⇒ $x = \frac{32000}{0.64}$

$\therefore x= 50,000$

So, the Present value of the table is Rs. 50,000

Application of Compound interest in population:

Compound interest is used to understand and predict population growth or decrease, as populations often grow or decrease like compound interest.

We can modify the compound interest formula to find the population growth.

The formula is: PPopulation after n years = $P (1\pm \frac{r}{100})^{nt}$,

Where P is the initial population,

R is the rate of interest per annum,

N = Number of terms rate is compounded,

and T is the time in years.

“+” will be used during the time of increase

“-” will be used during the time of decrease

Example:

The population of a village decreases at the rate of 40% per annum. If its population 2 years ago was 15,000, then find the present population.

Solution: The previous population ($x$) = 15000

The decrease rate ($r$) = 40%

Time ($t$) = 2 years

So, the present population

= $x(1-\frac{r}{100})^2$

= $15000(1-\frac{40}{100})^2$

= $15000×\frac{3}{5}×\frac{3}{5}$

= $5400$

So, the present population is 5400.

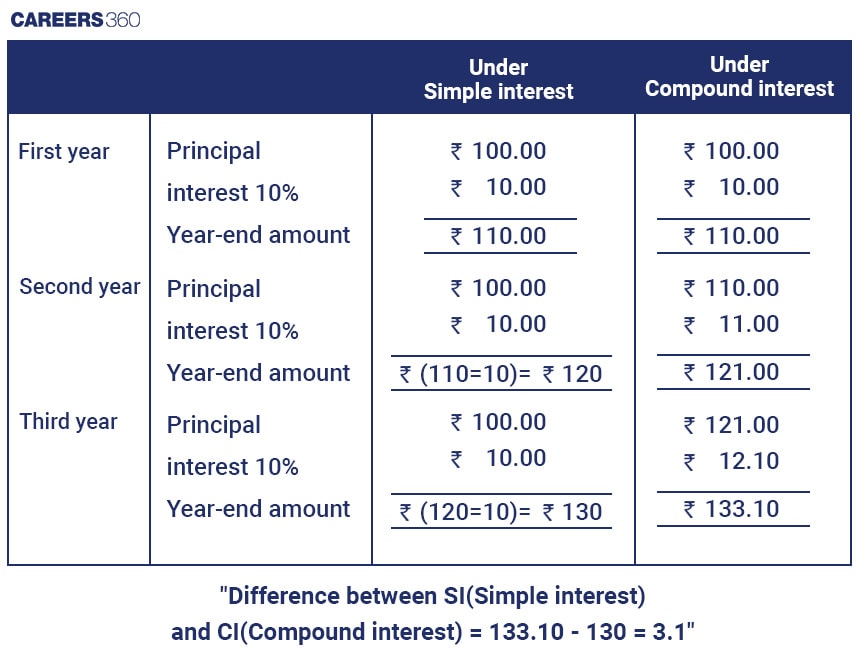
Difference between SI and CI

For the same amount of money for the same amount of time with the same rate of interest, if we calculate simple interest and compound interest consequently and subtract it from one another, then it is called the Difference between SI(Simple interest) and CI(Compound interest).

The below chart is an example of compound interest and simple interest for Rs. 100 for 3 years with a 10% interest rate.

Difference between SI and CI for two compounding cycles

To find the difference between simple interest and compound interest for two years, we can first find simple interest and compound interest for two years, then subtract simple interest from compound interest to get the difference.

There is a formula also to find it easily.

Difference between Compound interest and Simple interest for 2 years

= $P(\frac{R}{100})^2$,

where $P$ = Principal, $R$ = Rate of interest per cycle.

Example:

The difference between simple and compound Interest compounded annually on a certain sum of money for 2 years at 4% per annum is Rs. 8. The sum is:

Solution: Let the principal be Rs. $P$.

The rate of interest is $R$

Formula Used:

The difference between CI and SI for the same sum and same rate for 2 years = $\frac{PR^2}{10000}$

⇒ $8 =P\times \frac{4^2}{10000}$

⇒ $P = 5000$

Hence, the correct answer is Rs. 5,000.

Difference between SI and CI for three compounding cycles

To find the difference between simple interest and compound interest for 3 years, we can first find simple interest and compound interest for 3 years, then subtract simple interest from compound interest to get the difference. But that process is lengthy.

There is a formula also to find it easily.

Difference between Compound interest and Simple interest for 3 years

= $P×\frac{(300+R)R^{2}}{100^{3}}$,

where $P$ = Principal, $R$ = Rate of interest per cycle.

Example:

If the difference between compound interest and simple interest on a sum of money for 3 years is Rs. 186, find the sum of money, if the interest rate in both cases is 10%.

Solution: By applying the formula for finding the difference between CI and SI:

Difference = Principal$(\frac{\text{Rate}}{100})^2(\frac{\text{Rate}}{100}+3)$

⇒ 186 = Principal$(\frac{10}{100})^2(\frac{10}{100}+3)$

⇒ 186 = Principal$(\frac{1}{10})^2(\frac{1}{10}+3)$

⇒ 186 = Principal$(\frac{1}{100})(\frac{31}{10})$

$\therefore$ Principal = $(\frac{186×10×100}{31})$ = 6000

So, here the principal is Rs. 6,000.

Summary of all formulas used in Compound interest:

Let

A is the total amount,

P is the principal amount,

R is the rate of interest per annum,

N = Number of terms rate is compounded [Here it will be 4]

and T is the time in years.

Applications of Compound Interest in Real Life

• Compound interest is used in savings accounts in banks, where interests are often compounded daily, monthly, quarterly or yearly.

• It is also helpful to count the population if year by year or month by month population increases or decreases.

• Compound interest is used to find the values of items which are depreciated yearly, monthly or quarterly.

• Loans and mortgages often involve compound interest, where the interest is calculated on the principal amount plus any accumulated interest from previous periods.

• Compound interest calculations are often used in the Business sector to evaluate the potential growth of investments in new projects, equipment, or expansions.

Tips and Tricks

• If the compound interest rate is different for every year, then the formula is:

$P(1+\frac{R_1}{100})(1+\frac{R_2}{100})(1+\frac{R_3}{100}).......(1+\frac{R_n}{100})$,

Where P = Principal, R = Rate of interest, n = number of years

• Difference between Compound interest and Simple interest for 2 years formula is $=P(\frac{r}{100})^2$, where $P$ = Principal, $r$ = Rate of interest

• Difference between Compound interest and Simple interest for 3 years formula is $P×\frac{(300+R)R^{2}}{100^{3}}$, where $P$ = Principal, $R$ = Rate of interest.

• When compounded annually, $ A= P(1+\frac{R}{100})^{T}$, Where A is the total amount, P is the principal amount, R is the rate of interest per annum, and T is the time in years.

Solved Examples

Q1. At what time will Rs. 1000 become Rs. 1331 at 10% per annum compounded annually?

1. 3

2. $2\frac{1}{2}$

3. 2

4. $3\frac{1}{2}$

Hint: $\text{Total Amount}=\text{Principal}×(1+\frac{\text{Rate}}{100})^{\text{Time}}$

Answer:

Let the time be $n$.

We know, $\text{Total Amount}=\text{Principal}×(1+\frac{\text{Rate}}{100})^{\text{Time}}$

$⇒1331=1000(1+\frac{10}{100})^n$

$⇒1331=1000(\frac{110}{100})^n$

$⇒ \frac{1331}{1000}=(\frac{11}{10})^n$

$⇒ (\frac{11}{10})^3=(\frac{11}{10})^n$

After comparing, we get:

$n=3$

Hence, the correct answer is 3.

Q2. A man saves Rs. 2000 at the end of each year and invests the money at 5% compound interest. At the end of 3 years, he will have:

1. Rs. 4305

2. Rs. 6305

3. Rs. 4205

4. Rs. 2205

Hint: $\text{Total Amount}=\text{Principal}×(1+\frac{\text{Rate}}{100})^{\text{Time}}$, when interest is compounded annually.

Answer:

We know, $\text{Total Amount}=\text{Principal}×(1+\frac{\text{Rate}}{100})^{\text{Time}}$

$=2000(1+\frac{5}{100})^2+2000(1+\frac{5}{100})$

$=2000(\frac{21}{20})^2+2000(\frac{21}{20})$

$=2000\times \frac{441}{400}+2100$

$=2205+2100$

$=4305$

Amount after two years = Rs. 4305

$\therefore$ At the end of 3 years, he will have = 4305 + 2000 = Rs. 6305

Hence, the correct answer is Rs. 6305.

Q3. Find the amount that Shyam will get on Rs. 4096 if he gives it for 18 months at $12\frac{1}{2}$ percent per annum, with interest compounded half-yearly.

1. Rs. 5813

2. Rs. 4515

3. Rs. 4913

4. Rs. 5713

Hint: Amount = $P(1+\frac{\frac{R}{2}}{100})^{2n}$ where n is the time in years, where P is the principal, and R is the rate interest per annum compounded annually.

Answer:

Amount = $P(1+\frac{\frac{R}{2}}{100})^{2n}$ where n is the time in years, and where P is the principal, and R is the rate interest per annum compounded annually.

Principal = Rs. 4096

Time = 18 months = 3 half years

Rate R= $12\frac{1}{2}$ per annum% $\frac{R}{2}$⇒ $\frac{25}{4}%$ per half-year

Amount = $4096(1+\frac{25}{4 \times 100})^{3}$ = Rs. 4913

Hence, the correct answer is Rs. 4913.

Q4. The compound interest on Rs. 12000 for 9 months at 20% per annum, interest being compounded quarterly is:

1. Rs. 1,750

2. Rs. 1,891.50

3. Rs. 2,089.70

4. Rs. 2,136.40

Hint: Find the compound interest when interest is compounded quarterly, using the formula, $A = P × (1 + \frac{r}{n})^{n × t}$ where $A$ is the final amount, $P$ is the principal amount, $r$ is the annual interest rate, $n$ is the number of times the interest is compounded per year and $t$ is the number of years.

Answer:

Given: The Principal amount is Rs. 12,000, the annual interest rate (in decimal form) is 20% per annum, the number of times interest is compounded per year is 4 and the time the money is invested for (in years) is 9 months, which is $\frac{9}{12}=\frac{3}{4}$ years.

We know the formula, $A = P × (1 + \frac{r}{n})^{n × t}$.

Substitute the given values in the above formula, we get,

$A = 12000 × (1 + \frac{0.20}{4})^{4 × \frac{3}{4}}$

⇒ $A = 12000 × (1 + 0.05)^{3}$

⇒ $A = 12000 × (1.05)^{3}$

⇒ $A = 13891.5$

Compound interest is given as A – P.

= 13891.50 – 12000 = Rs. 1,891.50

Hence, the correct answer is Rs. 1,891.50.

Q5. The price of motorcycles depreciates every year by 10%. If the value of the motorcycle after 3 years will be Rs. 36,450, what is the present value (in Rs.) of the motorcycle?

1. 45,000

2. 50,000

3. 48,000

4. 51,000

Hint: Value after $n$ years $= x × (1-\frac{\text{R}}{100})^n$, where $x$ is the present value, $\text{R}$ is the rate of interest and $n$ is the time.

Answer:

Let the present value of a motorcycle be $x$.

Value after $n$ years $= x × (1–\frac{\text{R}}{100})^n$

Where $x$ is the present value, $\text{R}$ is the rate of interest and $n$ is the time.

Value after 3 years $= x × (1-\frac{\text{R}}{100})^3$

So, $36450 = x × (1-\frac{10}{100})^3$

⇒ $36450 = x × (\frac{9}{10})^3$

⇒ $x = 36450\times \frac{10\times 10 \times 10}{9 \times 9 \times 9}$

$\therefore x=50000$

So, the present value = Rs. 50,000

Hence, the correct answer is 50,000.

Q6. The population of a town increases each year by 4% of its total at the beginning of the year. If the population on 1st January 2001 was 500000, what was it on 1st January 2004?

1. 562432

2. 652432

3. 465223

4. 564232

Hint: The population after $n$ years can be calculated by using the formula $P(1+\frac{\text{R}}{100})^n$ where $P$ is the initial population, $R$ is the rate and $n$ is the time.

Answer:

The population after $n$ years can be calculated by using the formula $P(1+\frac{\text{R}}{100})^n$ where $P$ is the initial value, $R$ is the rate and $n$ is the time.

The population on 1st January 2001 was 500000.

Population after 3 years

$= 500000(1+\frac{4}{100})^3$

$= 500000(1+\frac{1}{25})^3$

$= 500000(\frac{26}{25})^3$

$= 500000 \times \frac{26}{25}\times \frac{26}{25}\times \frac{26}{25}$

$= 562432$

Hence, the correct answer is 562432.

Q7. On a certain sum of money, the difference between the compound interest for a year, payable half-yearly and the simple interest for a year is Rs. 180. If the rate of interest in both cases is 10%, then the sum is:

1. 60,000

2. 62,000

3. 72,000

4. 54,000

Hint: Find the SI and CI on the sum of money in terms of the principal. Then use the information to solve the question. Compound rate of interest half yearly =$ \frac{r}{2}$% and compound interest counted in a year are 2 times.

Answer:

Given:

When interest is calculated half yearly interest is halved i.e. 5%.

Number of period = 2

We know,

Simple interest, SI = $\frac{\text{Principal × Rate × Time}}{100}$

Compound Interest, CI = $P(1+\frac{R}{100})^{n}-P$, where $P$ is the principal, $R$ is the rate, and $n$ is the time period.

SI = $\frac{P \times 10 \times 1}{100} = \frac{P}{10}$

CI = $P((1+\frac{5}{100})^{2}-1) = P\times \frac{41}{400}$

According to the question,

$P\times\frac{41}{400}-\frac{P}{10}= 180$

⇒ $P\times\frac{1}{400} = 180$

$\therefore P = 72000$

Hence, the correct answer is Rs. 72000.

Q8. What is the compound interest earned on Rs. 80000 at 40% per annum in 1 year compounded quarterly?

1. Rs. 28317

2. Rs. 37128

3. Rs. 18732

4. Rs. 21387

Hint: Use the formula: when compounded annually, compound interest on Rs $P$ after n years at the rate of $R$% per annum compounded quarterly = $P \left(1+\frac{\frac{R}{4}}{100}\right)^{4n} - P$

Answer:

Given that:

$P = 80000, r = 40\%$ per annum and $n = 1$.

Compound Interest = $P \left(1 + \frac{\frac{R}{4}}{100}\right)^{4n} - P$

Where $P$ is the Principal amount (the initial amount of money), $R$ is the annual interest rate and $n$ is the year.

$⇒ CI= 80000 \left(1 + \frac{10}{100}\right)^4 - 80000$

$= 80000 (1.4641) - 80000$

$= 37128$

Hence, the correct answer is Rs. 37128

Q9. An amount was lent for two years at 20% per annum, compounded annually. Had the compounding been done half-yearly, the interest would have increased by Rs. 241. What was the amount (in Rs.) lent?

1. Rs. 10,000

2. Rs. 12,000

3. Rs. 20,000

4. Rs. 24,000

Hint: Find the Principal amount using the formula, $A = P(1 + \frac{r}{n})^{nt}$ where $A$ is the final amount, $P$ is the Principal amount, $r$ is the annual interest rate in decimal, $n$ is the number of times the interest is compounded per year and $t$ is the number of years.

Answer:

Given: An amount was lent for two years at 20% per annum, compounded annually. The difference in interest is Rs. 241.

We know the formula, $A = P(1 + \frac{r}{n})^{nt}$.

For compounding annually $(n = 1)$,

$A = P(1 + \frac{0.2}{1})^{1×2}$

⇒ $A = P(1.44)$

Now, we need to find the interest earned when compounding annually.

Interest annually = $A – P$

⇒ $P(1.44) – P = 0.44P$

The interest when compounding half-yearly $(n=2)$.

Interest half-yearly = $P(1 + \frac{r}{n})^{nt} – P$.

⇒ $P(1 + \frac{0.2}{2})^{2×2} – P = P(1.4641) – P= 0.4641P$

Interest half-yearly – Interest annually = Rs. 241

⇒ $(0.4641P) – 0.44P = 241$

⇒ $0.0241P = 241$

⇒ $P = \frac{241}{0.0241} = 10,000$

So, the amount lent (Principal amount) was Rs. 10,000.

Hence, the correct answer is Rs. 10,000.

Q10. The difference between compound interest and simple interest on an amount of Rs. 15,000 for 2 years is Rs. 96. The rate of interest per annum is:

1. 6%

2. 7%

3. 8%

4. 9%

Hint: Use the formula,

$D=P\left (\frac{r}{100}\right)^{2}$, where D is the difference between simple interest and compound interest for 2 years on Principal $P$ with the rate of interest $r$ per annum compounded annually.

Answer:

$D=P\left (\frac{r}{100}\right)^{2}$, where D is the difference between simple interest and compound interest for 2 years on Principal $P$ with the rate of interest $r$ per annum compounded annually.

⇒ $96 = 15000\left ( \frac{r}{100}\right )^{2}$

⇒ $r^2=\frac{960000}{15000}=64$

⇒ $r$ = 8%

Hence, the correct answer is 8%.