Divisibility Rules
Divisibility rules help us to determine if a number is divisible by another number without performing the actual division method.
In the actual division method, if a non-zero integer ‘a’ divides an integer ‘b’ and as a result, we get a number c, then we can say that b = ac. Here a is the divisor, b is the dividend, and c is the quotient.
If the number is not completely divisible, then there will be a remainder.
Dividend = Divisor × Quotient + Remainder
Rules of Divisibility or Divisibility Test in Maths
In divisibility rules(test) we find whether a given number is divisible by another number, we perform actual division and see whether the remainder is zero or not.
In mathematics, there are different rules of divisibility for every number. In this article, we will learn about them in detail.
Divisibility rule of 1
Every number is divisible by 1. So there is no particular divisibility rule for 1.
Example: 2 is divisible by 1, 100 is divisible by 1, etc.
Divisibility rule of 2
If the last digit of a number is even (i.e., 0, 2, 4, 6, 8), then the number is divisible by 2.
Example: 12 is divisible by 2, 24 is divisible by 2, 66 is divisible by 2, etc.
Divisibility rule of 3
If the sum of its digits of a number is divisible by 3, then that number is divisible by 3.
Example: 123 is divisible by 3 as the sum of the digits 1 + 2 + 3 = 6 is divisible by 3.
768 is divisible by 3 as the sum of the digits 7 + 6 + 8 = 21 is divisible by 3.
Divisibility rule of 4
If the last two digits of a number from left to right are divisible by 4, then that number is divisible by 4.
Example: 2064 is divisible by 4 as 64 is divisible by 4.
1532 is divisible by 4 as 32 is divisible by 4.
There is another way to check if a number is divisible by 4 or not. If the last two digits of a number are 0, then that number is divisible by 4.
Example: 600 is divisible by 4, 700 is divisible by 4, 1300 is divisible by 4, etc.
Divisibility rule of 5
If the last digit of a number is 0 or 5, then that number is divisible by 5.
Example: 125 is divisible by 5, 50 is divisible by 5, 575 is divisible by 5, etc.
Divisibility rule of 7
For 7 divisibility rule states that if a number is divisible by 7, then “the difference between twice the unit digit of the given number and the remaining part of the given number should be a multiple of 7 or it should be equal to 0”.
We have to take an example to understand it better.
Let's check if 2839155 is divisible by 7.
The unit digit of the number is 5.
So, 283915 – 5 × 2 = 283905
28390 – 5 × 2 = 28380
2838 – 0 = 2838
283 – 8 × 2 = 267
26 – 7 × 2 = 12, which is not divisible by 7.
So, the number is not divisible by 7.

Divisibility rule of 8
If the last three digits of a number from left to right are divisible by 8, then that number is divisible by 8.
Example: 151629664 is divisible by 8 as 664 is divisible by 8.
Divisibility rule of 9
For 9 divisibility rule states that if the sum of the digits of a number is divisible by 9, then that number is divisible by 9.
Example: 7363927 is divisible by 9 as the sum of the digits 7 + 3 + 6 + 3 + 9 + 2 + 6 = 36 is divisible by 9.
Divisibility rule of 10
If the last digit of a number is 0, then that number is divisible by 10.
Example: 100, 520, 630, 1000, etc.
Divisibility rule of 11
A number is divisible by 11 if the difference between the sum of the digits at even places and the sum of the digits at odd places of a number is either 0 or divisible by 11.
Example: 1726628 is not divisible by 11 as (1 + 2 + 6 + 8) - (7 + 6 + 2) = 2 is not divisible by 11.
3460831 is divisible by 11 as (3 + 6 + 8 + 1) - (4 + 0 + 3) = 11 is divisible by 11.
Divisibility rule of 13
The 13 divisibility rule states that to check if a number is divisible by 13, first, multiply the last digit/unit digit of the number by 4 and subtract it from the remaining number. Then check if it is divisible by 13. For larger numbers, use this process until you get a smaller number to check if it is divisible by 13 or not.
Let's check if 2639155 is divisible by 13.
The unit digit of the number is 5.
So, 263915 – 5 × 4 = 263895
26389 – 5 × 4 = 26369
2636 – 9 × 4 = 2600
260 – 0 × 4 = 260
26 – 0 × 4 = 26, which is divisible by 13.
So, the number is divisible by 13.

Divisibility rule of 16
If the last 4 digits of a number from left to right are divisible by 16, then the whole number is divisible by 16.
Example: 162652432 is divisible by 16 as 2432 is divisible by 16.
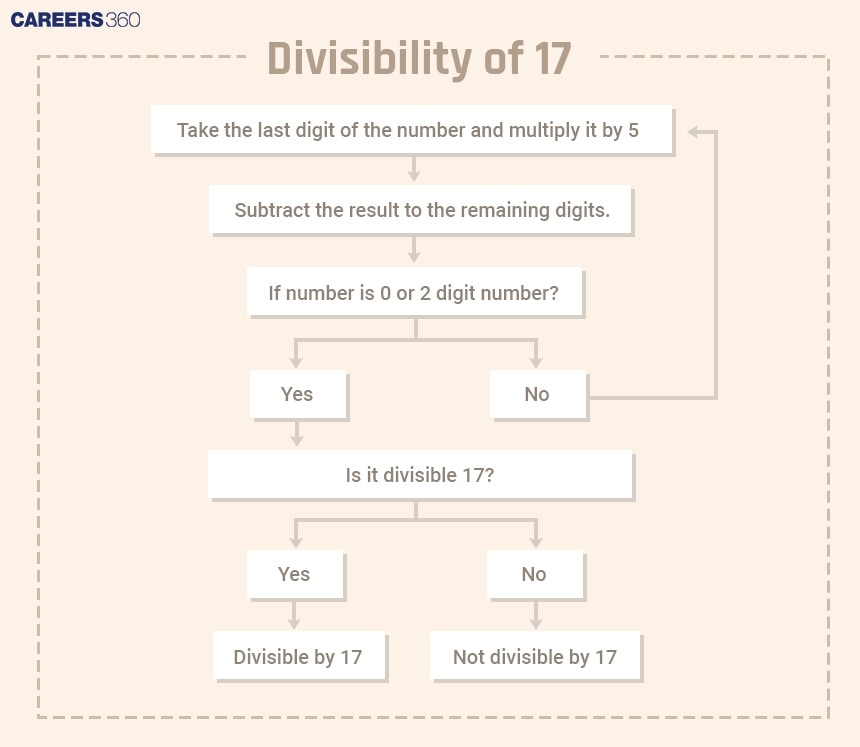
Divisibility rule of 17
First, multiply the last digit/unit digit of the number by 5 and subtract it from the remaining number. Check if it is divisible by 17. For larger numbers, use this process until you get a smaller number to check if it is divisible by 17 or not.
Let's check if 109718 is divisible by 17.
The unit digit of the number is 8.
So, 10971 – 5 × 8 = 10931
1093 – 5 × 1 = 1088
108 – 5 × 8 = 68, which is divisible by 17.
So, the number is divisible by 17.
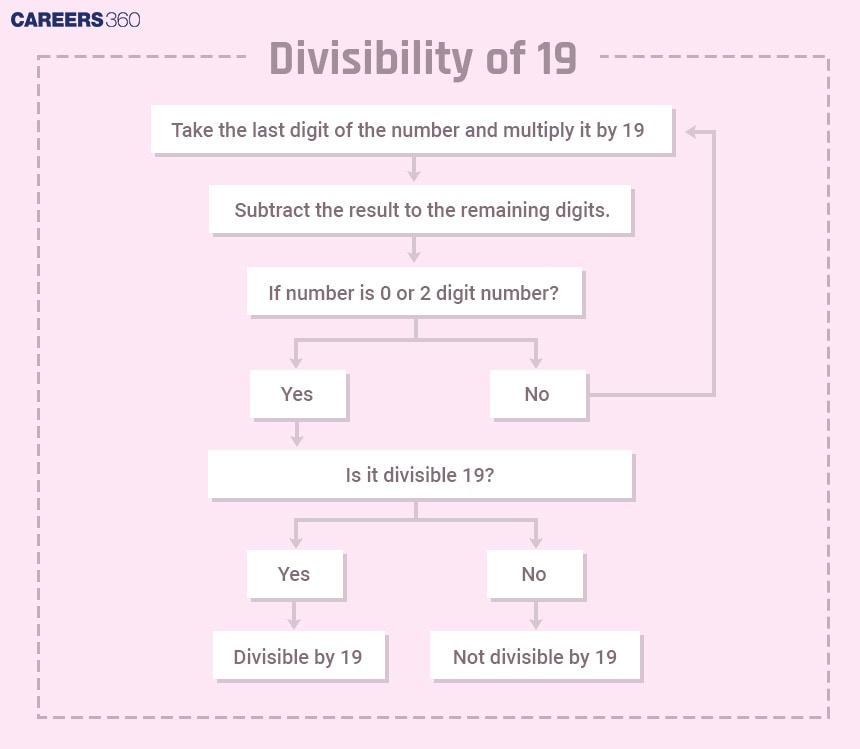
Divisibility rule of 19
First, double the last digit of the number and add it to the remaining number. Check if it is divisible by 19. For larger numbers, use this process until you get a smaller number to check if it is divisible by 19 or not.
Let's check if 2639155 is divisible by 7.
The unit digit of the number is 5.
So, 263915 + 5 × 2 = 263925
26392 + 5 × 2 = 26402
2640 + 2 × 2 = 2644
264 + 6 × 2 = 266
26 + 6 × 2 = 38, which is divisible by 19.
So, the number is divisible by 19.
Understanding the divisibility rule of 13, 17, and 19 with examples
The divisibility rule of 13, 17, and 19 is a bit complicated to remember. So we will take an example and check the same number is divisible by 13, 17, and 19.

Divisibility rules of 6, 12, 14, 15, 18 and of the numbers which are the product of two or more prime numbers
If a number is a multiple of two or more prime factors, then we have to that the number meets the divisibility rules for each of the prime factors. This systematic approach simplifies the process and ensures accuracy in determining divisibility.
Divisibility rule of 6: If a number is divisible by 2 and 3, then that number is divisible by 6.
- Example: 36 is divisible by 6 as it is divisible by 2 and 3.
Divisibility rule of 12: If a number is divisible by 3 and 4, then that number is divisible by 12.
- Example: 36 is divisible by 12 as it is divisible by 3 and 4.
Divisibility rule of 14: If a number is divisible by 2 and 7, then that number is divisible by 14.
- Example: 56 is divisible by 14 as it is divisible by 2 and 7.
Divisibility rule of 15: If a number is divisible by 3 and 5, then that number is divisible by 15.
- Example: 45 is divisible by 15 as it is divisible by 3 and 5.
Divisibility rule of 18: If a number is divisible by 2 and 9, then that number is divisible by 18.
- Example: 36 is divisible by 18 as it is divisible by 2 and 9.
CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts
XAT 2025: Section-wise Preparation Tips | Sample Paper
Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers
- Rules of Divisibility or Divisibility Test in Maths
- Understanding the divisibility rule of 13, 17, and 19 with examples
- Importance Of Divisibility Rules
- Divisibility: Tips and Tricks
- Practice Questions

Importance Of Divisibility Rules
Divisibility rules are a very integral part of mathematics for several reasons, providing both practical and theoretical benefits.
Simplifying Calculations:
The long division method is very time-consuming. Divisibility helps us to determine if a number is divisible by another number or not in less time and without the use of a calculator.
Example: 1756847577585 is divisible by 5, as we can see the last digit of the number is 5. However, using the long division method will take more time.
Factorisation:
The divisibility rule helps to factorise numbers and find LCM and GCD.
Example: To factorize 180, we can use the divisibility rules to find 2, 3, 5, and other factors quickly.
Problem-Solving:
In many mathematical problems, including puzzles and competitive examinations, we use the divisibility rule to find the answer quickly.
Programming and Algorithms:
In computer science, we use divisibility rules in algorithms for generating prime numbers, cryptography, and hashing.
Error Checking:
To find if a large number is divisible by 6, we can check if that number is divisible by 2 and 3.
Example: 1536 is divisible by 2(The last digit is even, i.e., 6) and 3(Sum of the digits, i.e., 15 is divisible by 3). So it will be divisible by 6.
Recognizing Composite Numbers:
If a number has more than two factors then it is called a composite number. Using the divisibility rule, we can easily check if a number is divisible by which numbers and recognize if it is a composite number or not.
Divisibility: Tips and Tricks
Memorize the basic divisibility rules of common numbers like 2, 3, 5, and 10. It will form a foundation for understanding more complex rules.
For numbers like 6, 12, or 15, use combinations of simpler rules. For 6, use the divisibility rule for 2 and 3.
If a number a is divisible by both b and c, then it is also divisible by their product b × c.
If a number a is divisible by b, and b is divisible by c, then a is also divisible by c.
If a number a is divisible by b and c, then it is divisible by their greatest common divisor.
Every leap is divisible by 4 but not every year divisible by 4 is a leap year.
Practice Questions
Q1. What is the smallest number that can be added to 9454351626 so that it becomes divisible by 11?
1
6
5
4
Hint: A number is divisible by 11 if the difference between the sum of the digits at even places and the sum of the digits at odd places of a number is either 0 or divisible by 11.
Answer:
A number is divisible by 11 if the difference between the sum of the digits at even places and the sum of the digits at odd places of a number is either 0 or divisible by 11.
Now, the difference between the sums = (9 + 5 + 3 + 1 + 2 − 4 − 4 − 5 − 6 − 6) = − 5
⇒ So, the difference is 5.
So, either we have to subtract 5 or add (11 – 5) = 6 to make 9454351626 divisible by 11.
Therefore, the smallest number that can be added to 9454351626 to make it divisible by 11 is 6.
Hence, the correct answer is 6.
Q2. Find the value of 'a' to make 6234a6 divisible by 9.
8
7
10
6
Hint: A number is divisible by 9 only when the sum of the digits of the number is divisible by 9.
Answer:
Given: The number is 6234a6.
A number is divisible by 9 when the sum of its digits is divisible by 9.
The sum of the digits of 6234a6 = 6 + 2 + 3 + 4 + a + 6 = 21 + a
The nearest value greater than 21 and divisible by 9 is 27.
So, 21 + a = 27
⇒ a = 6
Hence, the correct answer is 6.
Q3. Which of the following numbers is divisible by 8?
18718
18716
18712
18714
Hint: If the last three digits of a number are divisible by 8, then the number is divisible by 8.
Answer:
If the last three digits of a number are divisible by 8, then the number is divisible by 8.
Option 1: 18718. 718 cannot be divided by 8.
Option 2: 18716. 716 cannot be divided by 8.
Option 3: 18712. 712 is divisible by 8. Therefore, 18712 is also divisible by 8.
Option 4: 18714. 714 cannot be divided by 8.
Hence, the correct answer is 18712.
Q4. $4^{11}+4^{12}+4^{13}+4^{14}$ is divisible by:
7
14
17
9
Hint: Take $4^{11}$ common from the given expression.
Answer:
Given:
$4^{11}+4^{12}+4^{13}+4^{14}$
= $4^{11}(1+4+4^2+4^3)$
= $4^{11}(85)$
Since 85 is divisible by 17,
Therefore, the above expression is also divisible by 17.
Hence, the correct answer is 17.
Q5. Which of the following numbers is divisible by 99?
31548
60687
44775
84456
Hint: You have to check if the number is divisible by 9 and 11 to solve it.
Answer:
If a number is divisible by 99, then it must be divisible by 11 and 9, because 99 = 11 × 9
To check the divisibility by 11 we have to check the difference of the sum of odd place digits and the sum of even place digits.
If the result is 0 or a multiple of 11, then the number is divisible by 11.
To check the divisibility by 9, the sum of digits must be multiple of 9.
60687: Sum of odd place digits – Sum of even place digits = (6 + 6 + 7) – (0 + 8) = 11, which is divisible by 11.
Also, the sum of all digits = 6 + 0 + 6 + 8 + 7 = 27, which is divisible by 9.
So, 60687 will be divisible by 99.
Hence, the correct answer is 60687.
Q6. XY7B is a 4-digit number divisible by 4. What is the largest value of B?
6
2
0
8
Hint: For a number to be divisible by 4, the last 2 digits should be divisible by 4.
Answer:
For a number to be divisible by 4, the last 2 digits should be divisible by 4.
So, 7B should be divisible by 4.
76 is the largest number of the form 7B, which is divisible by 4.
Hence, the correct answer is 6.
Q7. The number 2918245 is divisible by which of the following numbers?
3
11
12
9
Hint: Divisibility rule for 3: A number is completely divisible by 3 if the sum of its digits is divisible by 3.
Divisibility rule for 11: The difference between the sum of digits at the odd position and the sum of digits at the even position in a number is 0 or 11.
Answer:
Given number: 2918245
Divisibility rule for 3: A number is completely divisible by 3 if the sum of its digits is divisible by 3.
Here, 2 + 9 + 1 + 8 + 2 + 4 + 5 = 31, which is not divisible by 3
⇒ The given number will not be divisible by 12 and 9 either.
Divisibility rule for 11: The difference between the sum of digits at the odd position and the sum of digits at the even position in a number is 0 or 11.
⇒ (2 + 1 + 2 + 5) – (9 + 8 + 4)
= 10 – 21
= –11, which is divisible by 11.
Hence, the correct answer is 11.
Q8. If the four-digit number 463y is divisible by 7, then what is the value of y?
4
6
3
5
Hint: First, divide the number by 7 and find the remainder. Then equate the remainder with 7 to find y.
Answer:
463y is divisible by 7.
463y = (7 × 661) + 3 + y
7 = 3 + y
⇒ y = 7 – 3 = 4
Hence, the correct answer is 4.
Q9. If the number 647592 is divisible by 88 and if the digits are rearranged in increasing order, then the new number thus formed will be divisible by:
22
66
44
3
Hint: If the sum of all digits of a number is divisible by 3 then the number will be divisible by 3.
Answer:
Given: The number 647592 is divisible by 88.
Rearranging the number in increasing order ⇒ 245679
Now, the sum of the digits = 2 + 4 + 5 + 6 + 7 + 9 = 33, which is divisible by 3.
So, the new number will be divisible by 3.
Hence, the correct answer is 3.
Q10. How many of the following numbers are divisible by 156?
312, 620, 936, 1402, 1872, 3216, 7176, 8108.
5
3
4
2
Hint: When we divide a number if we get the remainder as 0 then we can say that the given number is divisible by the divisor.
Answer:
Given numbers: 312, 620, 936, 1402, 1872, 3216, 7176, 8108.
312 = 156 × 2 + 0
620 = 156 × 3 + 152
936 = 156 × 6 + 0
1402 = 156 × 8 + 154
1872 = 156 × 12 + 0
3216 = 156 × 20 + 96
7176 = 156 × 46 + 0
8108 = 156 × 51 + 152
$\therefore$ A total of 4 numbers are divisible by 156.
Hence, the correct answer is 4.
Q11. If the 9-digit number $72 x 8431y 4$ is divisible by 36, what is the value of $(\frac{x}{y}-\frac{y}{x})$ for the smallest possible value of $y$, given that $x$ and $y$ are natural numbers?
$1 \frac{5}{7}$
$2 \frac{1}{10}$
$1 \frac{2}{5}$
$2 \frac{9}{10}$
Hint: First, check the divisibility of 4 and 9 and solve for $x$ and $y$. Then solve the required expression using it.
Answer:
If $72 x 8431y 4$ is divisible by 36,
Then, $72 x 8431y 4$ is divisible by 4 and 9.
Since it is divisible by 4, $y4$ is divisible by 4.
On putting $y=2, y4 = 24$ which is divisible by 4.
$\therefore$ The smallest possible value of $y$ is 2.
Now $72 x 8431y 4$ becomes $72 x 84312 4$
As it is divisible by 9,
$7+2+x+8+4+3+1+2+4=31+x$ is divisible by 9
⇒ $x=5$
$\therefore x=5, y=2$
$(\frac{x}{y}-\frac{y}{x})=(\frac{5}{2}-\frac{2}{5})=\frac{25-4}{10}=\frac{21}{10}=2\frac{1}{10}$
Hence, the correct answer is $2\frac{1}{10}$.
Q12. The number 150328 is divisible by 23. If the digits are rearranged in descending order and five times 13 is subtracted from the new number thus formed, then the resultant number will be divisible by:
3
5
11
2
Hint: The number 150328 is divisible by 23. When rearranged in descending order we get 853210. Now subtract 65 and then find out the number it can be divided by.
Answer:
Here, the number 150328 is divisible by 23.
When rearranged in descending order we get = 853210
When 5 times 13 i.e., 65 is subtracted from the new number, we get = 853210 – 65 = 853145
$\therefore$ The resultant number is divisible by 5 since the last digit is 5.
Hence, the correct answer is 5.
Q13. What are the values of R and M, respectively, if the given number is perfectly divisible by 16 and 11?
34R05030M6
4 and 6
7 and 5
5 and 5
5 and 7
Hint: A number is divisible by 16 if and only if the last 4 digits of the number are divisible by 16. A number is divisible by 11 if the difference of the sum of odd and even places is divisible by 11.
Answer:
Any number that has 4 or greater than 4 digits is divisible by 16 if and only if the last 4 digits of the number are divisible by 16.
Last 4 digits = 30M6
$\frac{30M6}{16}$ should be a whole number.
So M = 5 because $\frac{3056}{16}$ = 191
Now the number is 34R0503056
A number is divisible by 11 if the difference of the sum of odd and even places is divisible by 11.
To be divisible by 11,
$\frac{[(3 + R + 5 + 3 + 5) - (4 + 0 + 0 + 0 + 6)]}{11}$ should be a whole number
$=\frac{16+R-10}{11}$
$=\frac{6+R}{11}$
Hence, R must be 5 so that (6 + R) is divisible by 11.
Hence, the correct answer is 5 and 5.
Q14. If a 4-digit number x58y is exactly divisible by 9, then the least value of (x + y) is:
4
5
3
2
Hint: Divisibility rule of 9, which states that a number is divisible by 9 if the sum of its digits is divisible by 9.
Answer:
A number is divisible by 9 if the sum of its digits is divisible by 9.
Given a 4-digit number x58y, the sum of its digits is x + 5 + 8 + y = (x + y) + 13.
For the number to be divisible by 9, (x + y) + 13 must be divisible by 9.
The smallest possible value for (x + y) that makes (x + y) + 13 divisible by 9 is 5 (since 5 + 13 = 18, and 18 is the multiple of 9).
Hence, the correct answer is 5.
Q15. If the number 476xy0 is divisible by both 3 and 11, then in the hundredth and tenth places, the non-zero digits are, respectively:
2 and 3
3 and 2
5 and 8
8 and 5
Hint: A number is divisible by 3 if the sum of its digits is divisible by 3.
A number is divisible by 11 if the difference between the sum of digits at odd places and the sum of digits at even places is either 0 or divisible by 11.
Answer:
Let the given number be 476xy0.
Then (4 + 7 + 6 + x + y + 0) = (17 + x + y) must be divisible by 3.
And, (0 + x + 7) − (y + 6 + 4) = (x − y − 3) must be either 0 or 11.
From these conditions, we get x = 8 and y = 5.
Hence, the correct answer is 8 and 5.