Exponent and Surds: Definition, Calculator, Questions, Formula, Examples
Exponents and Surds: An Overview
Exponents and surds are very important fundamental mathematics concepts studied at various grades to build a strong foundation for advanced topics. In grade 11, students dive deeper into exponents and surds, exploring their properties and applications through detailed notes and examples. There are many resources that a student can find with names like "exponents and surds grade 11 pdf" and "exponents and surds grade 11 notes pdf". These rescources provide comprehensive explanations and practice problems. Grade 12 students will face more complex problems, as seen in "exponents and surds grade 12 questions and answers pdf," which help solidify their understanding. For students in lower grades, such as those in grades 9 and 10, introductory materials like “exponents and surds grade 10 pdf”, “exponents and surds grade 9 pdf” and also exponents and surds worksheets are available to introduce these concepts gradually. Practice problems and solutions, such as those in “exponents and surds questions and solutions”, "indices problems and solutions" and "indices problems and solutions pdf," are essential for mastering the manipulation and simplification of expressions involving exponents and surds.
CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts
XAT 2025: Section-wise Preparation Tips | Sample Paper
Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers
- Exponents of a real number
- Laws of Exponents
- What is a Surd?
- Types of Surds
- Laws of Surds
- Simplification Surds
- Tips and Tricks
- Practice Questions
Exponents of a real number
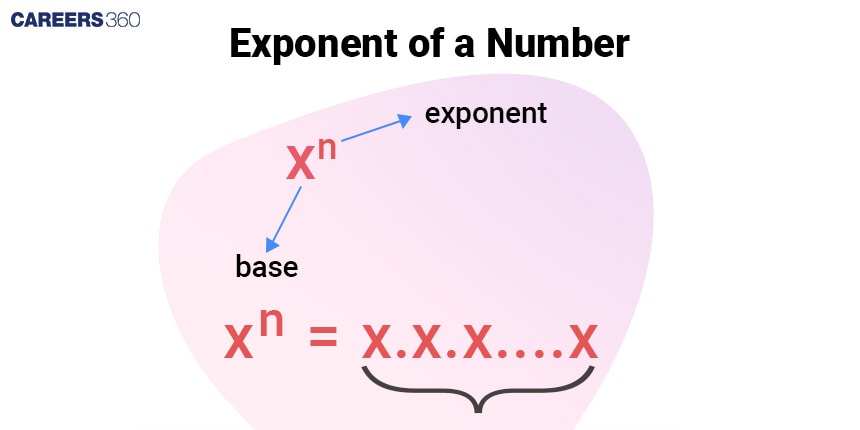
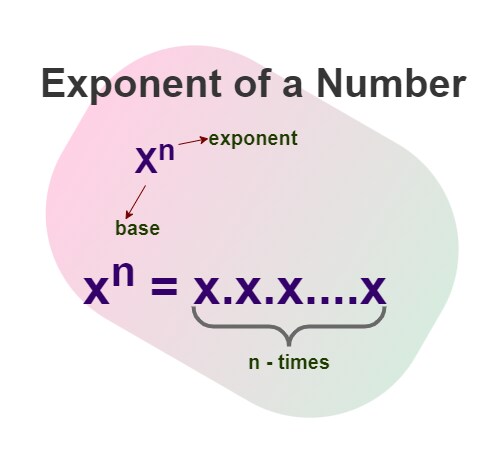
Exponents of a real number represent the multiplication of the base number. They can be positive, negative, zero or fractional. Some of the types are:
Positive exponents
Negative exponents
Zero exponents
Rational exponents
We have discussed thoroughly these exponents below.
Positive Exponents
If an exponent indicates how many times a number is multiplied by itself, it is called a Positive exponent.
Example:
3 × 3 × 3 = 33 = 9
Here 33 shows how many times the number 3 is multiplied by itself. So it is a Positive exponent.
Negative Exponents
If an exponent represents the reciprocal of the base raised to the absolute value of the exponent, then it is called a Negative exponent.
Example:
3-3 = $\frac{1}{3^3}=\frac{1}{9}$
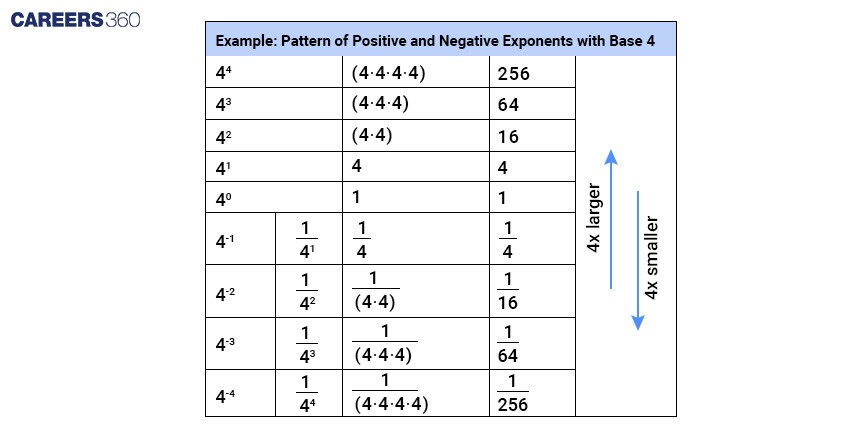
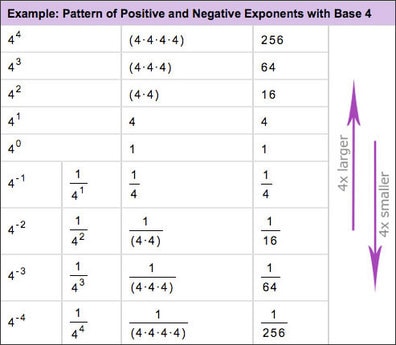
Zero Exponent
Any number with an exponent of zero has a value equal to 1.
Example:
50 = 1, 100 = 1, (-3)0 = 0, etc.
Rational Exponents
Rational exponents are also known as Fractional exponents. It represents both roots and powers.
Example: am/n is equivalent to the nth root of a raised to the power m.
163/4 = $(\sqrt[4]{16})^3$ = 23 = 8
Laws of Exponents
Here, a, b $\neq$ 0 | ||
Product law | When multiplying two exponents with the same base, exponents add. | am × an = amn |
Quotient law | When dividing two exponents with the same base, we subtract the exponents. | $\frac{a^m}{a^n}$ = am – n |
Power of power law | When raising a power to another power, we multiply the exponents. | (am)n = amn |
Power of product law | When raising a product to a power, we apply the exponent to each factor in the product. | (ab)m = am × bm |
Power of a quotient law | When raising a quotient to a power, we apply the exponent to the numerator and the denominator. | $(\frac{a}{b})^m= \frac{a^m}{b^m}$ |
Zero exponent law | Any non-zero base raised to the power of zero is equal to one. | a0 = 1 |
Negative exponent law | A negative exponent represents the reciprocal of the base raised to the positive exponent. | a–m = $\frac{1}{a^m}$ |
Fractional exponent law | A fractional exponent indicates a root where the numerator is the power, and the denominator is the root. | ax/y = $\sqrt[y]{a^x}$ |
Example 1:
Which value among $3^{200},2^{300},$ and $7^{100}$ is the largest?
$3^{200}=(3^{2})^{100}=9^{100}$
$2^{300}=(2^{3})^{100}=8^{100}$
$7^{100}=(7^{1})^{100}=7^{100}$
Thus, the largest number is $3^{200}$.
Example 2:
If $\left (\sqrt{5} \right)^{7}\div \left (\sqrt{5} \right)^{5}=5^{p},$ then the value of $p$ is:
Given: $\frac{(\sqrt{5})^7}{(\sqrt{5})^5} = 5^p$
$⇒(\sqrt{5})^{7 - 5} = 5^p$
$⇒(\sqrt{5})^2 = 5^p$
$⇒5^{\frac{1}{2}×2} = 5^{p}$
$⇒5^1=5^p$
Comparing both sides, we get,
$\therefore p=1$
Laws of Rational Exponents
Rational exponents, also known as fractional exponents, follow similar laws to integer exponents. These laws help simplify and solve expressions involving roots and powers.
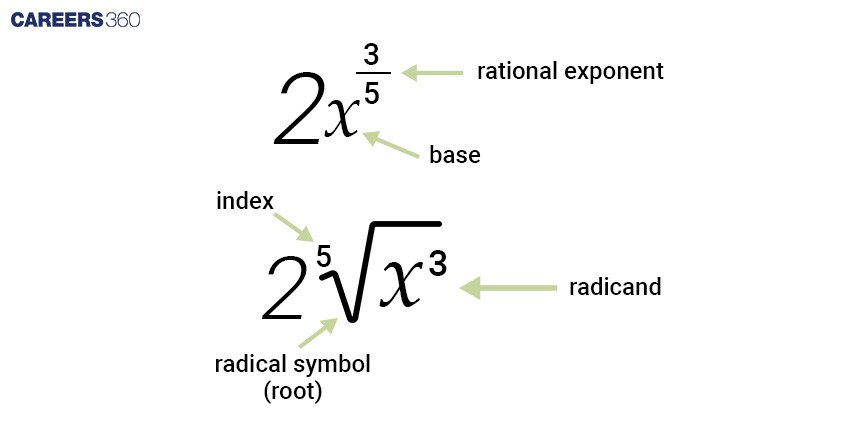
Here, m, n, p, q $\neq$ 0 | ||
Product law | When multiplying two rational exponents with the same base, exponents add. | ${a^{\frac mn}}×{a^{\frac pq}}=a^{\frac mn+\frac pq}$ |
Quotient law | When dividing two rational exponents with the same base, we subtract the exponents. | $\frac{a^{\frac mn}}{a^{\frac pq}}=a^{\frac mn-\frac pq}$ |
Power of power law | When raising a power to another power with rational exponents, we multiply the exponents. | $(a^{\frac mn})^{\frac pq}=a^{\frac mn×\frac pq}$ |
Power of product law | When raising a product to a rational exponent, we apply the exponent to each factor in the product. | $(ab)^\frac mn=a^{\frac mn} ×b^{\frac mn}$ |
Power of a quotient law | When raising a quotient to a rational exponent, we apply the exponent to the numerator and the denominator. | $(\frac ab)^\frac mn=\frac{a^{\frac mn}}{b^{\frac mn}}$ |
Fractional exponent law | A fractional exponent indicates a root where the numerator is the power, and the denominator is the root. | $a^{\frac mn}=\sqrt[n]{a^m}=(\sqrt[n]a)^m$ |
Example:
The value of $\frac{(243)^\frac{n}{5}\times 3^{2n+1}}{9^{n}\times 3^{n-1}}$ is:
Given: $\frac{(243)^\frac{n}{5}\times 3^{2n+1}}{9^{n}\times 3^{n-1}}$
= $\frac{(3^5)^\frac{n}{5}\times 3^{2n+1}}{3^{2n}\times 3^{n-1}}$
= $\frac{3^n\times 3^{2n+1}}{3^{2n}\times 3^{n-1}}$
= $\frac{3^{3n+1}}{3^{3n-1}}$
= $\frac{3^{3n}×3^1}{3^{3n}×3^{-1}}$
= ${3^{2}}$
= $9$
Hence, the value is 9.
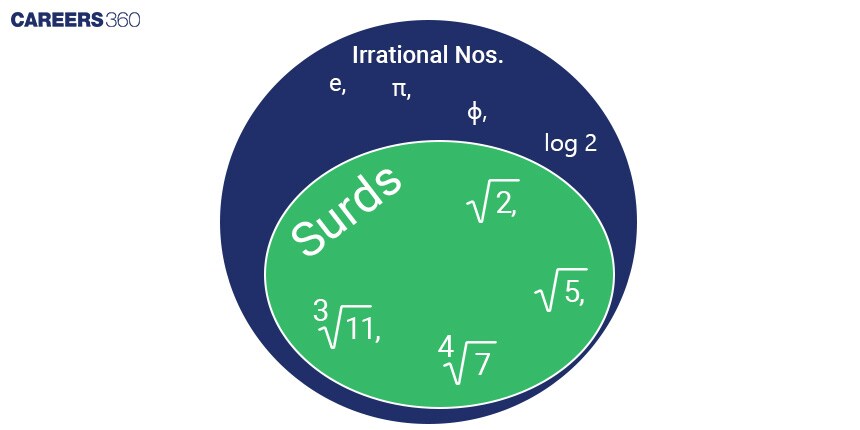
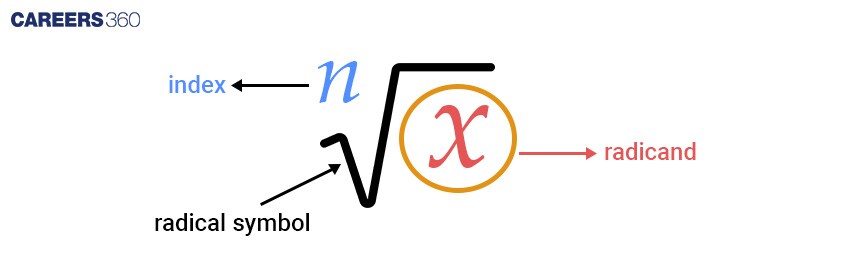
What is a Surd?
A surd is an irrational number which can not be simplified into a whole number or rational number after the square root or cube root of the number. It is not a perfect square or perfect cube number.
Example: $\sqrt{2}, \sqrt[3]{10}, \sqrt[4]{20},$ etc.
Types of Surds
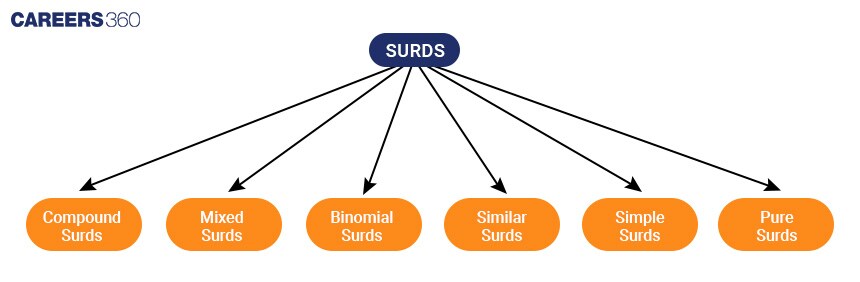
Simple Surds
Basic irrational numbers that are roots of integers that consist of only one term are called Simple Surds.
Example: $\sqrt2, \sqrt5,\sqrt7,$ etc.
Pure Surds
Surds that are entirely in the root form without any rational number coefficient are called Pure surds. Pure surds can not be written in a fraction form.
Example: $\sqrt{11}, \sqrt{13}, \sqrt{21},$ etc.
Mixed Surds
Surds that are mixed with rational numbers and irrational numbers are called Mixed Surds.
Example: $\sqrt[4]{7}, \sqrt[5]{3}, \sqrt[9]{6},$ etc.
Compound Surds
The sum or difference of two or more surds is called Compound surd.
Example: $(\sqrt3 + \sqrt7 + \sqrt{17}), (\sqrt8 - \sqrt[5]{3}),$ etc
Similar Surds
Surds with the same radicand(number under the roots) are called Similar surds. So it can be easily added or subtracted by combining the exponents.
Example: $2\sqrt5 + 3\sqrt5 = 5\sqrt5$
Binomial Surds
A compound surd consisting of only two terms is called a Binomial Surd.
Example: $(\sqrt6 - \sqrt[5]{9}), (\sqrt5 + \sqrt[2]{12}),$ etc.
Laws of Surds
Important laws of Surds | ||
Multiplication | During the multiplication of two surds, we can multiply the numbers inside the roots and take the square root of the number. | $\sqrt a × \sqrt b=\sqrt{ab}$ |
Division | During the division of two surds, we can divide the numbers inside the roots and take the square root of the quotients. | $\frac{\sqrt a}{\sqrt b}=\sqrt{\frac ab}$ |
Addition and Subtraction | We can add or subtract surds if they have the same radicand. Then we can combine or subtract the coefficient and keep the common surd. | $a\sqrt b + c \sqrt b=(a+c)\sqrt b$ $a\sqrt b - c \sqrt b=(a-c)\sqrt b$ |
Rationalize the denominator | To rationalize the denominator of a surd, multiply the numerator and denominator by a suitable surd that makes the denominator a rational number. | Let b be a rational number. $\frac{1}{\sqrt b}$ Then, $\frac{1×\sqrt b}{\sqrt b×\sqrt b} = \frac{\sqrt b}{b}$ |
Conjugate surds | If we have a binomial surd in the denominator, multiply the numerator and denominator by its conjugate to rationalize. | Conjugate of $(a+\sqrt b)$ is $(a-\sqrt b)$. Then, $\frac{1}{a+\sqrt b}=\frac{(a-\sqrt b)}{(a+\sqrt b)(a-\sqrt b)}$ |
Simplification Surds
Simplification of surds means converting the surds into a simple form, where the number inside the roots or radicands contains no square factors other than 1.
This process needs some steps which are explained below.
Step 1: Break down the number inside the roots into its prime factors.
Step 2: Pair the prime factors.
Step 3: Take out pairs of prime factors from under the square root, as they become whole numbers.
Example:
Simplify $\sqrt{24}$.
$\sqrt{24}=\sqrt{2×2×2×3}=\sqrt{2^2×2×3}=2\sqrt{2×3}=2\sqrt6$
Simplify $4\sqrt{75}$.
$4\sqrt{75}=4\sqrt{5×5×3}=4\sqrt{5^2×3}=4×5\sqrt{3}=20\sqrt3$
Tips and Tricks
Any number with an exponent of zero has a value equal to 1.
am/n is equivalent to the nth root of a raised to the power m.
$\sqrt a × \sqrt b=\sqrt{ab}$
Let b be a rational number.
$\frac{1}{\sqrt b}$
Then,
$\frac{1×\sqrt b}{\sqrt b×\sqrt b} = \frac{\sqrt b}{b}$
Conjugate of $(a+\sqrt b)$ is $(a-\sqrt b)$.
am × an = amn
$\frac{a^m}{a^n}$ = am – n
For surds, simplify the radicand, combine like terms, rationalize denominators, and use surd properties for simplification.
For Exponents, memorize and apply the laws of exponents, and practice simplifying complex expressions.
Practice Questions
Q1. If $(2^{3})^{2} = 4^{x}$, then $3^{x}$ is equal to:
3
6
9
27
Hint: Use the indices rule: if $a^x = a^y$, then $x=y$
Answer:
Given: $(2^{3})^{2} = 4^{x}$
⇒ $2^{6} = 2^{2x}$
⇒ $6 = 2x$ (If $a^x = a^y$, then $x=y$)
⇒ $x = 3$
$\therefore$ $3^{x} = 3^{3} = 27$
Hence, the correct answer is 27.
Q2. If $4^{(x+y)} = 256$ and $(256)^{(x–y)} = 4$, what are the values of $x$ and $y?$
$\frac{17}{8}$ and $\frac{15}{8}$
$\frac{17}{4}$ and $\frac{15}{4}$
$\frac{9}{17}$ and $\frac{15}{17}$
$\frac{8}{17}$ and $\frac{8}{15}$
Hint: Use the indices rule: if $a^x = a^y$, then $x=y$
Answer:
Given: $4^{(x+y)}=256$
⇒ $4^{(x+y)} = 4^4$
⇒ $x+y = 4$
⇒ $x = 4-y$-----(1)
And $(256)^{(x-y)}=4$
⇒ $(4^4)^{(x-y)}=4^1$
⇒ $4x-4y =1$-----(2)
Putting the value of $x$ from equation (1), we get,
$4(4-y)-4y = 1$
⇒ $16-4y-4y =1$
$\therefore y =\frac{15}{8}$
Now, substituting the value of $y$ in equation (1), we get,
$x = 4-\frac{15}{8}$
$\therefore x = \frac{17}{8}$
Hence, the correct answer is $\frac{17}{8}$ and $\frac{15}{8}$.
Q3. The value of $(x^{\frac{1}{3}}+x^{-\frac{1}{3}})(x^{\frac{2}{3}}-1+x^{-\frac{2}{3}})$ is:
$x^{-1}+x^{\frac{2}{3}}$
$x+x^{-\frac{1}{3}}$
$x^{\frac{1}{3}}+x^{–1}$
$x+x^{–1}$
Hint: Multiply both the terms and use the rule of indices: $a^x \times a^y = a^{x+y}$
Answer:
Given: $(x^{\frac{1}{3}}+x^{-\frac{1}{3}})(x^{\frac{2}{3}}-1+x^{-\frac{2}{3}})$
$=x^{\frac{1}{3}}×x^{\frac{2}{3}}-x^{\frac{1}{3}}+x^{\frac{1}{3}}×x^{-\frac{2}{3}}+x^{-\frac{1}{3}}×x^{\frac{2}{3}}-x^{-\frac{1}{3}}+x^{-\frac{1}{3}}×x^{-\frac{2}{3}}$
$=x^{\frac{1}{3}+\frac{2}{3}}-x^{\frac{1}{3}}+x^{\frac{1}{3}-\frac{2}{3}}+x^{-\frac{1}{3}+\frac{2}{3}}-x^{-\frac{1}{3}}+x^{-\frac{1}{3}-\frac{2}{3}}$
$=x^1-x^{\frac{1}{3}}+x^{-\frac{1}{3}}+x^{\frac{1}{3}}-x^{-\frac{1}{3}}+x^{-1}$
$=x+x^{-1}$
Hence, the correct answer is $x+x^{-1}$.
Q4. If the numbers $\sqrt[3]{9}, \sqrt[4]{20}$ and $\sqrt[6]{25}$ are arranged in ascending order, then the right arrangement is:
$\sqrt[6]{25}<\sqrt[4]{20}< \sqrt[3]{9}$
$\sqrt[3]{9}<\sqrt[4]{20}<\sqrt[6]{25}$
$\sqrt[4]{20}<\sqrt[6]{25}<\sqrt[3]{9}$
$\sqrt[6]{25}<\sqrt[3]{9}<\sqrt[4]{20}$
Hint: Simplify the given values by taking the least common multiple (LCM) of the roots to make roots equal, then compare to find the desired value.
Answer:
Given: The numbers are $\sqrt[3]{9}$, $\sqrt[4]{20}$, $\sqrt[6]{25}$.
LCM of 3, 4, and 6 = 12
$⇒ \sqrt[3]{9}=9^{\frac{1}{3}}=9^{\frac{4}{12}}=\sqrt[12]{6561}$
$⇒ \sqrt[4]{20}=20^{\frac{1}{4}}=20^{\frac{3}{12}}=\sqrt[12]{8000}$
$⇒ \sqrt[6]{25}=25^{\frac{1}{6}}=25^{\frac{2}{12}}=\sqrt[12]{625}$
By comparing these values, we get:
$\sqrt[12]{625}<\sqrt[12]{6561}<\sqrt[12]{8000}$
$⇒\sqrt[6]{25}<\sqrt[3]{9}<\sqrt[4]{20}$
Hence, the correct answer is $\sqrt[6]{25}<\sqrt[3]{9}<\sqrt[4]{20}$.
Q5. What is the value of $\left[\frac{12}{(\sqrt5+\sqrt3)}+\frac{18}{(\sqrt{5}-\sqrt3)}\right]$?
$15(\sqrt5–\sqrt3)$
$3(5\sqrt5+\sqrt3)$
$15(\sqrt5+\sqrt3)$
$3(3\sqrt5+\sqrt3)$
Hint: Use the formula: $(\sqrt a+\sqrt b)(\sqrt a–\sqrt b) = a-b$
Answer:
Given:
$\left[\frac{12}{(\sqrt5+\sqrt3)}+\frac{18}{(\sqrt{5}-\sqrt3)}\right]$
= $\frac{12\sqrt5-12\sqrt 3+18\sqrt5+18\sqrt 3}{(\sqrt5+\sqrt3)(\sqrt{5}-\sqrt3)}$
= $\frac{30\sqrt5+6\sqrt3}{5-3}$
= $\frac{6(5\sqrt5+\sqrt3)}{2}$
= $3(5\sqrt5+\sqrt3)$
Hence, the correct answer is $3(5\sqrt5+\sqrt3)$.
Q6. The quotient when $10^{100}$ is divided by $5^{75}$ is:
$2^{25}×10^{75}$
$10^{25}$
$2^{75}$
$2^{75}×10^{25}$
Hint: Solve by using the formula: $\frac{a^{m}}{a^{n}}=a^{(m-n)}$ and simplify to find the unknown value.
Answer:
Given: $10^{100}$ is divided by $5^{75}$.
= $\frac{10^{100}}{5^{75}}$
= $\frac{(2×5)^{100}}{5^{75}}$
= $\frac{2^{100}×5^{100}}{5^{75}}$
= $2^{100}×\frac{5^{100}}{5^{75}}$
By using, $\frac{a^{m}}{a^{n}}=a^{(m–n)}$
= $2^{100}×5^{(100-75)}$
= $2^{100}×5^{25}$
= $2^{75}×2^{25}×5^{25}$
= $2^{75}×10^{25}$
Hence, the correct answer is $2^{75}×10^{25}$.
Q7. What is the value of the given expression?
$\frac{4^{a + 4}- 5 \times 4^{a + 2}}{15 \times 4^a - 2^2 \times 4^a}$
16
64
20
24
Hint: Use the information below to solve the problem.
$x^{ab}=x^a×x^b$
Answer:
$\frac{4^{a+ 2}(4^{2} - 5 \times 1)}{4^{a}(15 - 4)}$
$=\frac{4^{a + 2}(11)}{4^{a}(11)}$
$=\frac{4^{a}\times4^{2}(11)}{4^{a}(11)}$
$=4^2$
$=16$
Hence, the correct answer is 16.
Q8. If $a=b^p,b=c^q,c=a^r$, then $pqr$ is:
1
0
-1
abc
Hint: Use the values of $b$ and $c$ in the equation $a=b^p$.
Answer:
Given:
$a=b^p,b=c^q,c=a^r$
$a=b^p$
⇒ $a=(c^q)^p$
⇒ $a=(a^r)^{pq}$
⇒ $a^1=(a)^{pqr}$
$\therefore pqr=1$
Hence, the correct answer is 1.
Q9. When xm is multiplied by xn product is 1. The relation between m and n is:
mn = 1
m = n
m + n = 1
m = – n
Hint: Use the following formula to solve the question:
xm × xn = xm + n
Answer:
xm × xn = 1
⇒ xm + n = x0
⇒ m + n = 0
⇒ m = –n
Hence, the correct answer is m = – n.
Q10. If $2^{2x-y}=16$ and $2^{x+y}=32$, the value of $xy$ is:
2
4
6
8
Hint: If am = an, then m = n.
Answer:
Given: $2^{2x-y}=16$
$⇒2^{2x-y}=2^4$
$⇒2x-y=4$--------------------(1)
Again, $2^{x+y}=32$
$⇒2^{x+y}=2^5$
$⇒x+y=5$ ---------------------(2)
Solving equations (1) and (2), we get:
$x=3$ and $y= 2$
$\therefore xy=3×2=6$
Hence, the correct answer is $6$.
Frequently Asked Questions (FAQs)
Surd | Exponent |
Surds involve roots and represent irrational numbers that cannot be simplified to exact fractions. | Exponents involve raising a number to a power and following specific arithmetic rules, resulting in either rational or irrational numbers. |
Surds can not written as a whole number. | Exponents can be written as a whole number. |
Example: $\sqrt2$, $\sqrt3$ | Example: an, where n is the exponent |
Yes, it is a surd.
As we know a surd is an irrational number that can not be simplified into a whole number or rational number after the square root or cube root of the number. It is not a perfect square or perfect cube number.
Here $\sqrt 7$ can not be simplified into a whole number or rational number after the square root or cube root of the number. Hence it is a surd.
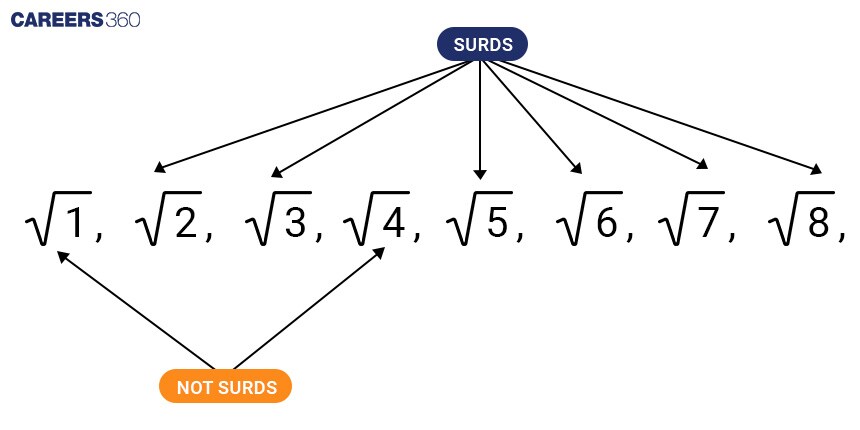
Number | Decimal | Surd or Not Surd |
$\sqrt2$ | 1.4142…. | Surd |
$\sqrt3$ | 1.73205…. | Surd |
$\sqrt4$ | 2 | Not Surd |
$\sqrt[3]{125}$ | 5 | Not Surd |
$\sqrt[3]{25}$ | 2.9240… | Surd |
Exponents of a real number represent the multiplication of the base number. They can be positive, negative, zero or fractional. Some of the types are:
Positive exponents: 52 = 25
Negative exponents: 5–2 = $\frac{1}{5^2}=\frac{1}{25}$
Zero exponents: 50 = 1
Rational exponents: 163/2= $(\sqrt[2]{16})^3=4^3=64$
A surds form does not have negative numbers. Surds can only have positive numbers, decimals, and fractions.
Surds can be fractions. $\sqrt{\frac{2}{3}}$