Last Two Digit of a number

The tens place and the unit digit of a number are called the last two digits of a number.

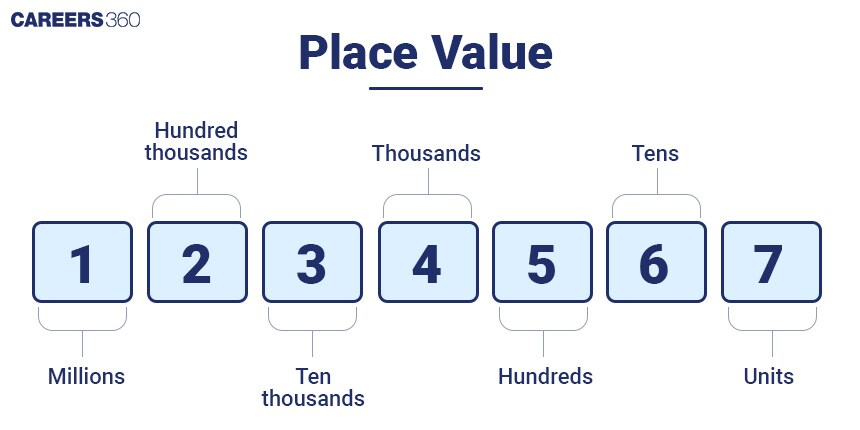
In the number 15732, 3 is the tens place digit and 2 is the units place digit. These two combined can be called the Last two digits of a number.

Also, 7 is the hundreds place digit, and 5 is the thousands place digit.

That number can be written as 15 thousand 7 hundred thirty-two.

Understand the basics: The last two digits of the product of two numbers

If we multiply two numbers, then in the resultant number the tenth place digit and unit digit are together called the Last two digits of the product of two numbers.

If we multiply 12 and 15, as a result, we get 180.
Here 80 is the last two digits.

But most of the time there will be two bigger numbers to multiply and it will be hard to know the last two digits of the product of those two numbers. That's why we will use modulo 100 for calculation to get the last two digits.
The step-by-step calculation is given below for better understanding.

Steps to calculate the last two digits of the product of two numbers

Step 1: Take the last two digits of the two numbers

First, take the last two digits of the two numbers (tenth place digit and unit digit).
Example: In the numbers 65577 and 687876, the last two digits are 77 and 76.

Step 2: Multiplication

Now, multiply those two numbers.

Example: 77 × 76

Step 3: Use the modulo 100

The result of those two numbers modulo 100 will give us the last two digits of the original number.

Modulo 100 means if we divide the result of the multiplicated number by 100, the remainder is called modulo 100.

It is written as “mod 100”.

Let's take an example to understand it better:

Find the last two digits of the product 8377484 and 98848848.

Here, the last two digits of the numbers are 84 and 48

84 × 48 = 4032

Now, 4032 mod 100 ≡ 32 as dividing 4032 by 100 will give us a remainder of 32.

Hence, the last two digits of the products 8377484 and 98848848 are 32.

To find the last two digits of a number in the form xⁿ:

To find the last two digits of a number in the form xⁿ, we will use modular arithmetic operations to make it simpler.
We will learn that step by step.

Step 1: Identification of the unit digit

First, we have to identify the unit digit of base x.

Step 2: Converting the last digit

Then, if the last digit is 3, 4, or 7, convert it into a number where the last digit will be 1.

If the last digit is 2, 4, or 8, then convert it into a number where the last digit is 1, 3, 5, 7 and then process with the same process.
For example, 84 can be written as 21 × 4, 72 can be written as 8 × 9.

For numbers ending with 5 and 6, there are some rules which we will discuss later.

Example: Find the last two digits of 17²³.

Here, the last digit is 7.

So, we will break it into the form of 17⁴.
17²³

= (17)^{4 × 5} × 17³

Taking 17⁴, we get,

The last two digits of 17⁴ = 21

Also, the last two digits of 17³ = 13

Now, (21)⁵ × 13

Any number ending with 1, will also have 1 in their unit digit when it will have power above.

To find the 2nd last digit, we have to multiply the ten’s place digit of the base and unit digit of the power and take their unit digit.

Here, the last digit is 1.

2nd last digit of (21)5 will be 0 as 2 × 5 = 10.

Finally, 01 × 13 = 13

Hence, the last two digits of 17²³ is 13.

The last two digits of a number in the form of
x² / (50 + x)² / (50 – x)² / (100 + x)² / (100 – x)²

x²

(50 + x)² = 2500 + 100x + x²

(50 – x)² = 2500 – 100x + x²

(100 + x)² = 10000 + 200x + x²

(100 – x)² = 10000 – 200x + x²

As we can see from above the last two digits of (50 + x)² / (50 – x)² / (100 + x)² / (100 – x)² will be the same as the last digit of x².

Let’s take an example.

Suppose x = 2.

So, x²= 2² = 4

Here, the last two digits are 04.

Now, putting the value of x in (50 + x)² / (50 – x)² / (100 + x)² / (100 – x)², we get,

So, we can see that the last two digits are the same as that of x².

The last two digits of a number in the form of oddⁿ (Except 5)

The last two digits of numbers end with 1, 3, 7, and 9.

Numbers ending with 1

Any number ending with 1, will also have 1 in their unit digit when it will have power above.

To find the 2nd last digit, we have to multiply the ten’s place digit of the base and unit digit of the power and take their unit digit.

Let's take an example to understand it better.

Find the last two digits of 61⁸⁴.

Here the unit digit will be 1.

2nd last digit = 6 × 4 = 24 ( We will take 4, as it is the unit digit of the multiplication)

Hence, the last two digits of 61⁸⁴ is 41.

Numbers ending with 3

If the last digit of a number is 3, then we have to break the exponent into the form of 34. Then the last digit will be 1, and it will be easily solved.

Let's take an example.

Find the last two digits of 43⁸⁴.

First, we have to break it into the form of 43⁴.

43⁸⁴

= 43^{(4 × 21)}

Taking 43⁴, we get,

The last two digits of 43⁴ is 01.

Now, (01)²¹

Here, the last digit of (01)²¹ is 1.
2nd last digit of (01)²¹ is 0 × 2 = 0

So, the last two digits of 43⁸⁴ are 01.

Numbers ending with 7

If the last digit of a number is 7, then we have to break the exponent into the form of 74. Then the last digit will be 1, and it will be easily solved.

Let's take an example.

Find the last two digits of 47³⁵.

47³⁵

= (47)^{4 × 8} × 47³

Taking 474, we get,

The last two digits of 47⁴ = 81

Also, the last two digits of 47³ = 23

Now,

The last two digits of 47³⁵ = last two digits of (81)⁸ × 23

Here, the last digit is 1.
2nd last digit of (81)⁸ will be 4 as 8 × 8 = 64.

Finally, 41 × 23 = 943

Hence, the last two digits of 47³⁵ are 43.

Numbers ending with 9

If the last digit of a number is 9, then we have to break the exponent into the form of 92. Then the last digit will be 1, and it will be easily solved.

Let's take an example.

Find the last two digits of 8964.

89⁶⁴

= 89^{2 × 32}

Taking 89², we get,

The last two digits of 89² = 21

Now, (21)³²

Here, the last digit is 1.

2nd last digit of 89⁶⁴ is 4 as 2 × 2 = 4

Hence, the last two digits of 89⁶⁴ are 41.

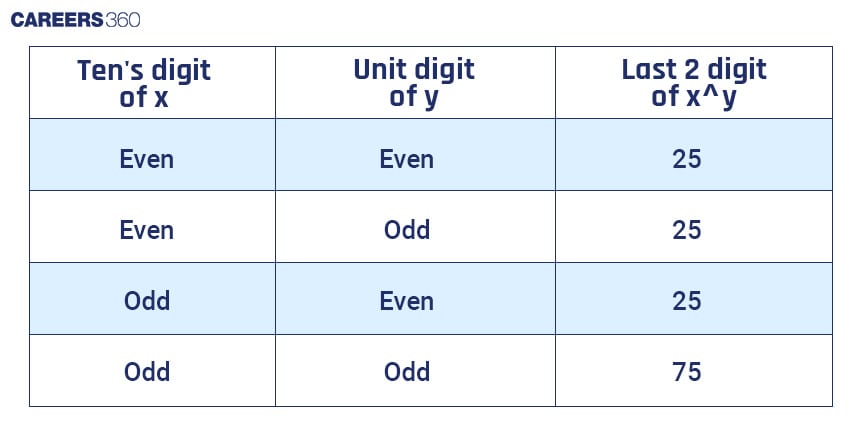
The last two digits of a number of the form (odd 5 )ⁿ

If the number ends with 5 and the tens digit of the base and the unit digit of the exponent are both odd then the last two digits of the number will be 75.

Example:

The last two digits of 575⁸⁷ are 75.

The last two digits of 235⁵⁹ are 75.

If the number ends with 5, the tens digit of the base is odd and the unit digit of the exponent is even then the last two digits of the number will be 25.
Example:

The last two digits of 535⁸⁸ are 25.

The last two digits of 795⁵⁶ are 25.

The last two digits of a number of the form (even 5)ⁿ

If the number ends with 5, the tens digit of the base is even and the unit digit of the exponent is odd then the last two digits of the number will be 25.
Example:

The last two digits of 165⁴³ are 25.

The last two digits of 685¹²³ are 25.

If the number ends with 5, the tens digit of the base is even and the unit digit of the exponent is even then the last two digits of the number will be 25.
Example:

The last two digits of 545⁸⁸ are 25.

The last two digits of 725⁵⁶ are 25.

This is a table to find the last two digits of a number where the unit digit is 5.

The last two digits of a number of the form (even)ⁿ

The last two digits of numbers end with 2, 4, 6, and 8.

Numbers ending with 2

(210)^odd, then the last two digits will be 24.

(210)^even, then the last two digits will be 76.

If we multiply 76 with 2ⁿ, the last two digits will be 2ⁿ.

Example:

1. Find the last two digits of 2²³.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

This Story also Contains

1. Understand the basics: The last two digits of the product of two numbers
2. Steps to calculate the last two digits of the product of two numbers
3. To find the last two digits of a number in the form xn:
4. Tips and Tricks
5. Practice questions

( 2²⁰)¹ × 2³

= (2¹⁰)² × 8

The last two digits of (2¹⁰)² is 76.

So, 76 × 8 = 608

Hence, the last two digits of 2²³ is 08.

2. Find the last two digits of 2⁵⁴.

( 2⁵⁰)¹ × 2⁴

= (2¹⁰)⁵ × 16

The last two digits of (2¹⁰)⁵ is 24.

So, 24 × 16 = 384

Hence, the last two digits of 2⁵⁴ is 84.

Numbers ending with 4

Numbers ending with 4 can be converted to numbers ending with 1. This will help us to find the last two digits faster.

Also, we can convert them into the power of 2’s. Then use the formulae of numbers ending with 2.

Example: 44 = 4 × 11, 84 = 4 × 21, 64 = 2⁶ etc.

If the number is not a multiple of 4, then it can be converted with numbers ending with 6, 7, and 8. Then we will solve them.

Example: 74 = 2 × 37, 94 = 2 × 47 etc.

Let’s take an example to understand it better.

Find the last two digits of 84⁵⁴.

(4 × 21)⁸⁴

= (2²)⁸⁴ × (21)⁸⁴

= 2¹⁶⁸ × (21)⁸⁴

Taking 2¹⁶⁸

= (2¹⁰)¹⁶ × 2⁸

The last two digits of (2¹⁰)¹⁶ is 76 and the last two digits of 2⁸ are 56.

Now, the last two digits of 76 × 56 = 56

Taking (21)⁸⁴

Here, the unit digit is 1, and the ten's place digit will be 2 × 4 = 8

So, the last two digits = 81

Finally,

56 × 81 = 4536

Hence, the last two digits of 84⁵⁴ are 36.

Numbers ending with 6

Numbers ending with 6 will always have a factor 2 in them as 2 × 3 = 6.

So, we will convert them into numbers ending with 2.

Then,

(2¹⁰)^odd, then the last two digits will be 24.

(2¹⁰)^even, then the last two digits will be 76.

Example: 16²⁴ = (2⁴)²⁴ = 2⁹⁶ = (2¹⁰)⁹ × 2⁶

Let’s take an example of the whole process.

Find the last two digits of 76²⁰

76²⁰

= (4 × 19)²⁰

= 4²⁰ × 192⁰

= (2²)²⁰ × 19²⁰

= 2⁴⁰ × 19²⁰

= (2¹⁰)⁴ × 19²⁰

Now, the last two digits of (2¹⁰)⁴ are 76.

Taking 19²⁰ = (19)^2×10

Now, the last two digits of 19² is 61.

(61)¹⁰

Here, the last digit is 1.

2nd last digit is 0 as 6 × 0 = 0

Finally, 76 × 01 = 76

Hence, the last two digits of 76²⁰ is 76.

Numbers ending with 8

Numbers ending with 8 can be converted to numbers ending with 1, 3, 7, and 9. This will help us to find the last two digits faster.

Example:

Find the last two digits of 28³⁴.

28³⁴

= (4 × 7)³⁴

= (2²)³⁴ × 7³⁴

= 2⁶⁸ × 7³⁴

= (2¹⁰)⁶ × 2⁸ × 7³⁴

The last two digits of (2¹⁰)⁶ are 76.

2⁸ = 256

If we multiply 76 by 2⁸, then the last two digits will be the last two digits of 2⁸ i.e., 56

7³⁴

= (7)^{4 × 8} × 7²

Taking 7⁴, we get,

The last two digits of 7⁴ is 01.

Also, 7² = 49

Now, (01)⁸ × 49

Here, the last digit is 1.
2nd last digit is 0 as 0 × 8 = 0

So, 01 × 49 = 49

Finally, we get, 56 × 49 = 2744

Hence, the last two digits of 28³⁴ are 44.

Tips and Tricks

• We can convert the numbers ending with 2, 4, 6, and 8 into numbers ending with 1, 3, 5, and 7 by taking 2’s outside of the bracket.

• If we multiply 76 with 2ⁿ, the last two digits will be 2ⁿ.

• The last two digits of 76ⁿ, where n is a positive integer will always be 76.

• If numbers have the last two digits of 24, then the square of that number will have 76 as the last two digits.

• Numbers ending with 1 always have 1 in the unit digit.

• To find the last two digits of the product of two larger numbers, we can use modulo 100.

Practice questions

Q1. Find the last two digits of 17¹²³.

1. 13

2. 23

3. 43

4. 03

Answer:

Here, the last digit is 7.

17¹²³

= (17)^{4 × 30} × 17³

Taking 17⁴, we get,

The last two digits of 17⁴ = 21

Also, The last two digits of 17³ = 13

Now, (21)³⁰ × 13

Here, the last digit is 1.

2nd last digit is 0 as 2 × 0 = 0

Finally, 01 × 13 = 13

Hence, the last two digits of 17123 are 13.

Q2. Find the last two digits of 89¹⁰².

1. 22

2. 21

3. 20

4. 25

Answer:

Here, the last digit is 9.

89¹⁰²

= (89)^{2 × 51}

Taking 89², we get,

The last two digits of 89² = 21

Now, (21)⁵¹

Here, the last digit is 1.

2nd last digit is 2 as 2 × 1 = 2

Hence, the last two digits of 89¹⁰² are 21.

Q3. Find the last two digits of 251¹⁸.

1. 01

2. 11

3. 21

4. 15

Answer:

Here, the last digit is 1.

So, the unit digit of the last two digits will be 1.

To find the ten's digit, we will multiply the ten's digit of the base with the unit digit of the power.

5 × 8 = 40 (Here the last digit is 0)

Hence, the last two digits of 251¹⁸ are 01.

Q4. Find the last two digits of 93²⁵.

1. 43

2. 93

3. 63

4. 83

Answer:

Here, the last digit is 3.

93²⁵

= (93)^{4 × 6} × 93

Taking 93⁴, we get,

The last two digits of 93⁴ = 01

Now, (01)⁶ × 93

= 1 × 93

= 93

Hence, the last two digits of 93²⁵ are 93.

Q5. Find the last two digits of 45³³.

1. 25

2. 75

3. 05

4. 55

Answer:

Here, the last digit is 5.

Here ten's digit of the base is even and the unit digit of the exponent is odd.

So, the last two digits will be 25.

Hence, the last two digits of 45³³ are 25.

Q6. Find the last two digits of 35³³.

1. 75

2. 25

3. 35

4. 05

Answer:

Here, the last digit is 5.

Here ten's digit of the base is odd and the unit digit of the exponent is also odd.

So, the last two digits will be 75.

Hence, the last two digits of 35³³ are 75.

Q7. Find the last two digits of 78²⁵.

1. 78

2. 68

3. 58

4. 08

Answer:

78²⁵

= (2 × 39)²⁵

= 2²⁵ × 39²⁵

= (2¹⁰)² × 2⁵ × 39²⁵

We know,

(2¹⁰)^even, then the last two digits will be 76.

The last two digits of (76 × 2⁵) is 32.

39²⁵

= (39)^{2 × 12} × 39

Taking 39², we get,

The last two digits of 39² is 21.

Now, (21)¹² × 39

Here, the last digit is 1.

2nd last digit is 4 as 2 × 2 = 4

So, The last two digits of (41 × 39) are 99.

Finally, we get, 32 × 99 = 3168

Hence, the last two digits of 78²⁵ are 68.

Q8. Find the last two digits of 16²⁵.

1. 86

2. 66

3. 06

4. 76

Answer:

16²⁵

= (2⁴)²⁵

= 2¹⁰⁰

= (2¹⁰)¹⁰

As we know, when the power of 2¹⁰ is even, the last two digits will be 76.

Hence, the last two digits of 16²⁵ are 76.

Q9. Find the last two digits of 64⁷³.

1. 24

2. 04

3. 44

4. 14

Answer:

64⁷³

= (2 × 32)⁷³

= 2⁷³ × 32⁷³

= (2¹⁰)⁷ × 2³ × (2⁵)⁷³

= (2¹⁰)⁷ × 2³ × 2³⁶⁵

= (2¹⁰)⁷ × 2³ × (2¹⁰)³⁶⁰ × 2⁵

Taking (2¹⁰)⁷, the last two digits are 24.

Taking (2¹⁰)³⁶⁰, the last two digits are 76.

So, The last two digits of (24 × 8 × 76 × 32) are 44.

Hence, the last two digits of 64⁷³ are 44.

Q10. Find the last two digits of 2⁷³.

1. 02

2. 92

3. 84

4. 12

Answer:

2⁷³

= (2¹⁰)⁷ × 2³

The last two digits of (2¹⁰)⁷ are 24.

So, 24 × 8 = 192

Hence, the last two digits of 2⁷³ are 92.