Linear Equations in Two Variables: Definition, Questions, Formula, Examples

Linear equations in two variables are a very important part of algebra. A Pair of Linear Equations in Two Variables means there are two such equations. Linear Equations in Two Variables Examples include systems like 2x + 4y = 5 and 4x + 7y = 6. To solve these, various Linear Equations in Two Variables with Solving Methods can be employed, such as substitution, elimination, cross multiplication, and graphical methods. The Pair Of Linear Equation In Two Variables solutions can be unique, infinite, or no solutions, depending on the relationships between the coefficients. Common Pair Of Linear Equations In Two Variables questions involve finding the point of intersection of the lines represented by the equations. The general Pair Of Linear Equation In Two Variables formula for the solution, if unique, is derived from these methods.

Definition

Linear equations are generally in the form of ax + by = c, where x and y are two variables and a, b, and c are constants. A Pair of Linear Equations in Two Variables means there are two such equations. a1x + b1 y = c1 and a2x + b2y = c2

Example: 2x + 5y = 6 and 5x + 8y = 9 are two pairs of linear equations.

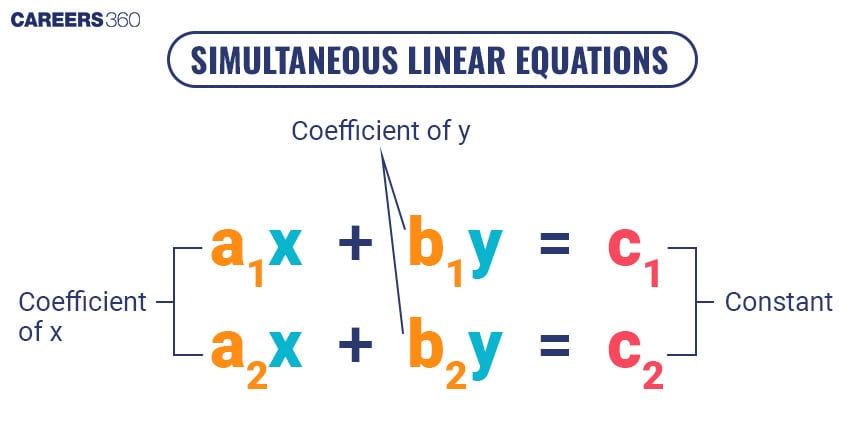
A standard form of Linear Equation in Two Variables

The standard form of a linear equation in two variables is:

ax + by = c, where x and y are two variables and a, b, and c are constants.

Solution of Linear Equation in Two Variable

Methods of solving Linear Equations in two Variable

There are many methods of solving linear equations in two variables. Some of them are as follows:

• Algebraic method (Substitution method and Elimination method)

• Graphical method

• Cross multiplication method

• Method of determinant

Algebraic Method

Algebraic method gives us a systematic approach to solving the pair of linear equations in two variables.

There are two main algebraic methods.

• Substitution method

• Elimination method

Let’s discuss these methods thoroughly.

Substitution Method

The substitution method involves picking one equation from the pair of linear equations in two variables and writing one variable in terms of the other. Then substitute that value in the other equation.

The steps to do the Substitution method are:

Let a pair of linear equations with two variables $x$ and $y$.

Step 1: First, pick any of the two equations and write the value of $x$ in terms of $y$.

Step 2: Substitute the value of $x$ in the other equation.

Step 3: Now find the value of $y$ as there is only one variable.

Step 4: Put the value of $y$ in any equation to find the value of $x$.

Example:

If $x+3y=-3x+y$, then $\frac{x^{2}}{2y^{2}}$ is equal to:

$x+3y+3x-y=0$

⇒ $4x+2y=0$

⇒ $2(2x+y)=0$

⇒ $2x+y=0$

⇒ $y=–2x$

Put the value of $y$ in $\frac{x^{2}}{2y^{2}}$

= $\frac{x^{2}}{2(–2x)^{2}}$

= $\frac{x^{2}}{8x^{2}}$

= $\frac{1}{8}$

Hence, the value of fraction = $\frac{1}{8}$ and value of y = -2x.

Elimination Method

The elimination method involves adding or subtracting the equations to eliminate one of the variables, making it possible to solve for the remaining variable. This method is vastly used and more convenient.

The steps to do the Elimination method are:

Step 1: Multiply one or both equations by a constant so that the coefficients of one of the variables are opposites.

Step 2: Now add or subtract to eliminate that variable.

Step 3: Find the value of the remaining variable as there is only one variable.

Step 4: Substitute the value in any of the equations to get the value of the other variable.

Example:

If a + b = 5 and a – b = 3, then the value of a and b is:

a + b = 5 -----------------------(i)

a – b = 3 ----------------------(ii)

Add both equations (i) and (ii),

⇒ a + b + a – b = 5 + 3

⇒ 2a = 8

⇒ a = 4

From equation (i),

⇒ 4 + b = 5

⇒ b = 5 – 4

⇒ b = 1

Hence, the value of a = 4 and b = 1.

Graphical Method

The graphical method visually shows the solution to a pair of linear equations by plotting the lines and finding their intersection point.

A pair of linear equations that are parallel and have no solution is called an inconsistent pair of linear equations.

A pair of linear equations with two variables that are intersecting and have a unique solution is called a Consistent pair of linear equations.

A pair of linear equations with two variables that are overlapping and have infinitely many solutions is called a Dependent pair of linear equations. A pair of dependent linear equations are always consistent.

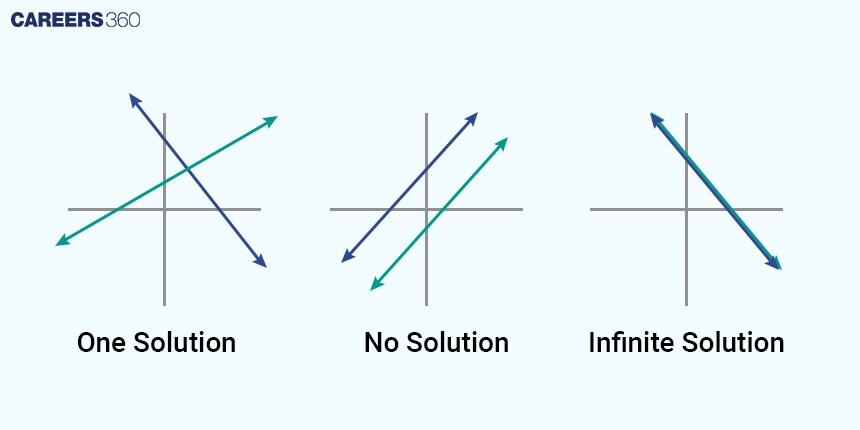
Example:

Check graphically if the given pair of linear equations is consistent. If so solve them graphically.

• $x + 3y = 6$

• $2x - 3y = 12$

Now, we have the points on the graph. A(0, 2), B(6, 0), P(0, -4), and Q(3, -2)

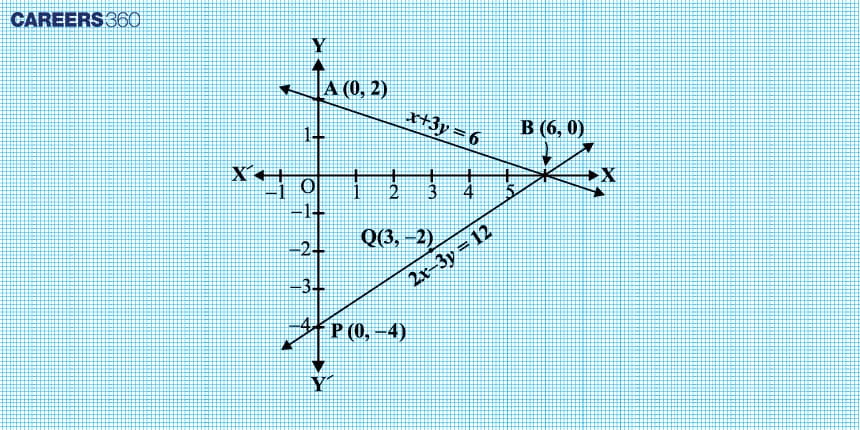
As we can see point B(6, 0) is common to both lines AB and PQ.

So, the solution of the pair of linear equations is $x$ = 6 and $y$ = 0

i.e., Given pair of linear equations are consistent.

Cross Multiplication Method

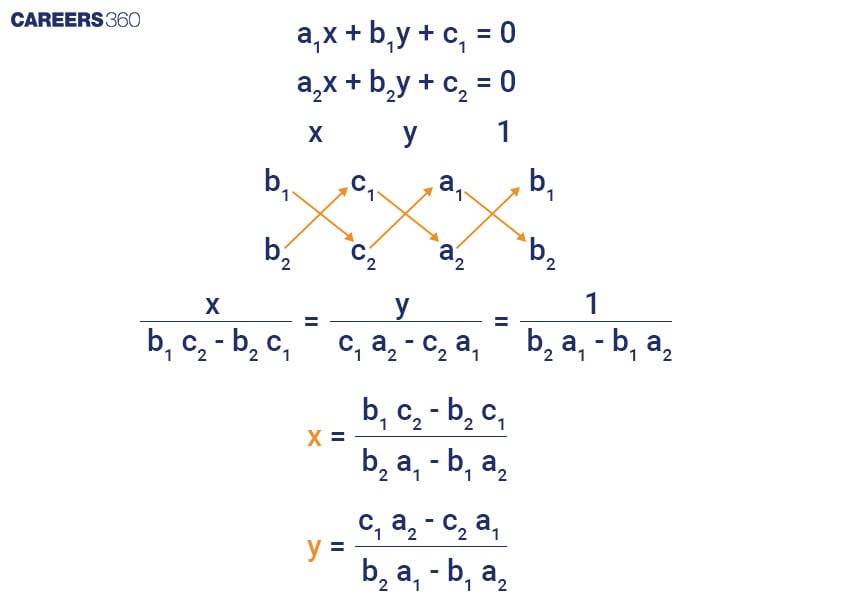
If a pair of linear equations are:

$a_1 x+b_1 y+c_1=0$ and $a_2 x+b_2 y+c_2=0$

Now, in cross multiplication method we can write these variables like

$\frac{x}{b_1c_2-b_2c_1}$ = $\frac{y}{c_1a_2-c_2a_1}$ = $\frac{1}{b_2a_1-a_1b_2}$

Finally, we get:

$x$ = $\frac{b_1c_2-b_2c_1}{b_2a_1-a_1b_2}$

And $y$ = $\frac{c_1a_2-c_2a_1}{b_2a_1-a_1b_2}$

The step-by-step process is given below to understand the process better.

Method of Determinant

The method of the determinant is also called Cramer’s rule. It is an algebraic method to solve pair linear equations using determinants. This method is particularly useful when dealing with systems that can be represented in matrix form.

Let’s discuss how deteminant works.

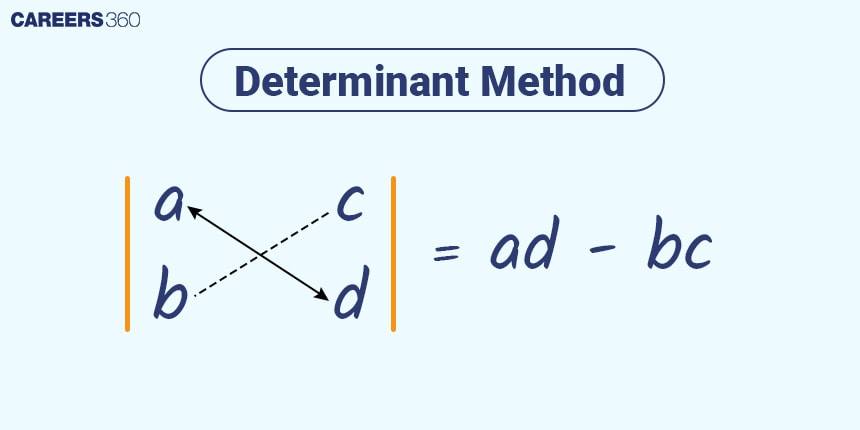
Now steps to do Cramer’s rule to solve a pair of linear equations.

Let's consider two linear equations.

a1x + b1 y = c1

a2x + b2y = c2

Step 1: Form a coefficient matrix and name it D.

Step 2: Form a determinant Dx, replacing the first column of the coefficient matrix D with the constants on the right side of the equations.

Step 3: Form a determinant Dy, replacing the 2nd column of the coefficient matrix D with the constants on the right side of the equations.

Step 4: To get the value of x, divide Dx by D and to get the value of y divide Dy by D.

Example:

Types of Solution

Linear equations can have three types of solutions.

• Unique solution

• No solution

• Infinite many solutions

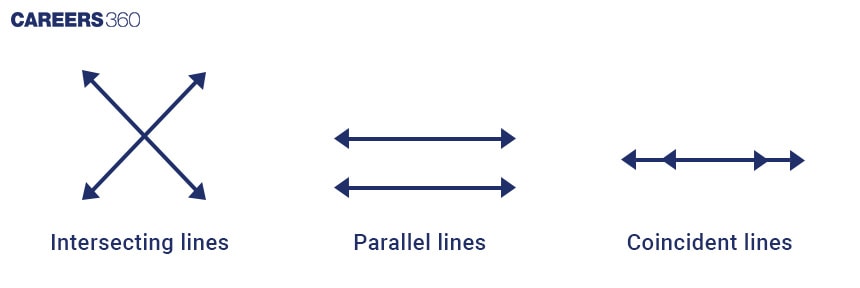
Let two linear equations with two variables be

a1x + b1 y = c1 and a2x + b2y = c2

We will check with these equations when and what type of solutions we get.

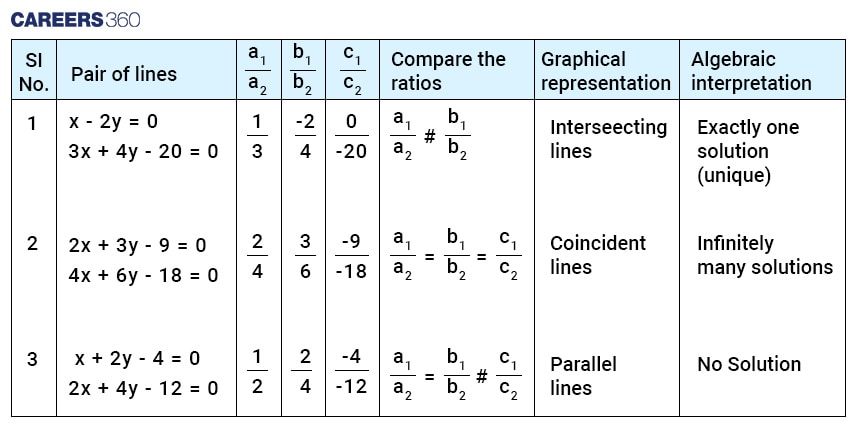
Unique Solution

If two lines intersect exactly at one point, then the system of equations has only one Unique solution.

Formula to check if two linear equations have a unique solution or not is:

$\frac{a_1}{a_2} \neq \frac{b_1}{b_2}$

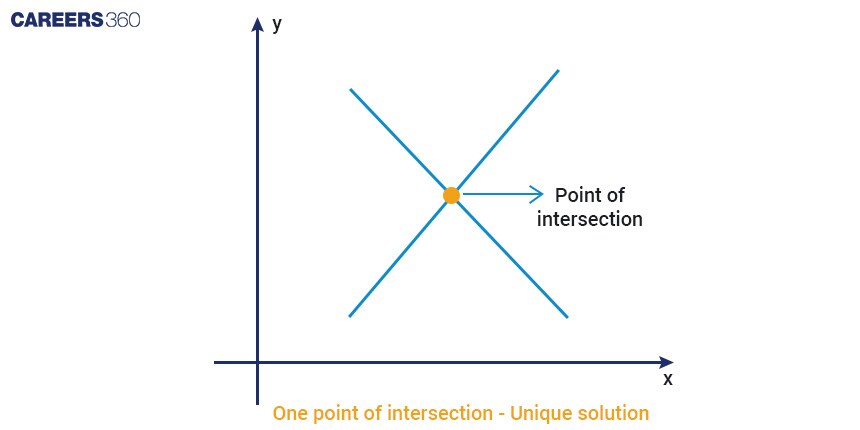
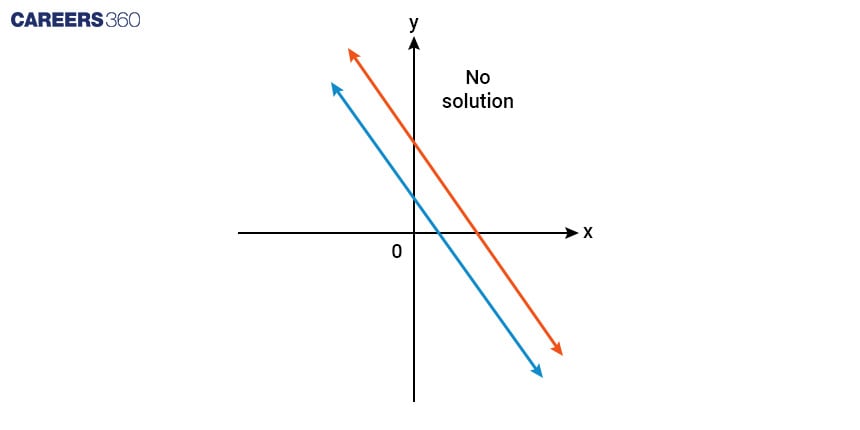
No Solution

If two lines are parallel and never intersect each other, then the system of equations has no solution.

In this case, the slopes of the two lines are the same but their intercepts are different.

Formula to check if two linear equations have no solution is:

$\frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2}$

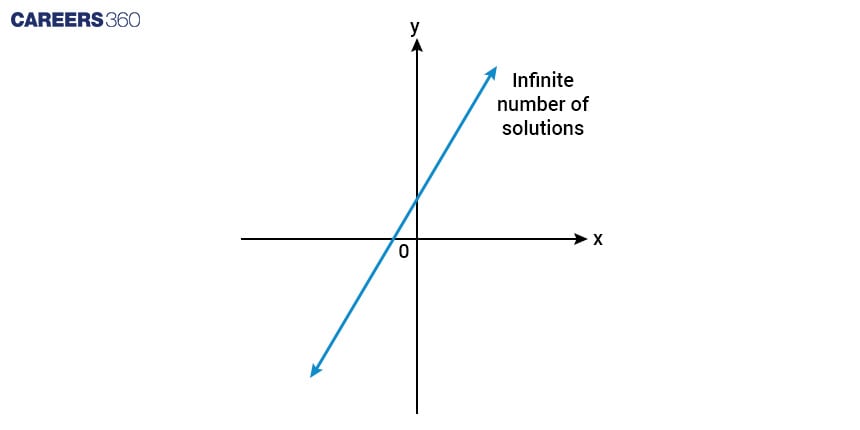
Infinite Many Solutions

If two lines coincide or stay on the same line and overlap completely, then the system of equations has infinitely many solutions.

Formula to check if two linear equations have infinitely many solutions or not is:

$\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}$

Summary of Solutions of two Linear Equations in two Variables

Tips and Tricks

If $a_1 x+b_1 y=c_1$ and $a_2 x+b_2 y=c_2$ are two linear equations, then

• $\frac{a_1}{a_2} \neq \frac{b_1}{b_2}$ to have a unique solution

• $\frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2}$ to have no solution.

• $\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}$ to have infinitely many solutions.

• Substitution method involves picking one equation from the pair of linear equations in two variables and writing one variable in terms of the other.

• The elimination method involves adding or subtracting the equations to eliminate one of the variables, making it possible to solve for the remaining variable.

• The graphical method visually shows the solution to a pair of linear equations by plotting the lines and finding their intersection point.

• Method of the determinant is particularly useful when dealing with systems that can be represented in matrix form.

Practice Questions

Q1. If a + b = 17 and a – b = 9, the value of (4a2 + 4b2) is:

1. 710

2. 720

3. 720

4. 740

Hint: From the two given equations find the values of a and b then put the values in the given expression to get the answer.

Answer:

Given:

a + b = 17------------ (i)

a – b = 9------------ (ii)

Adding equation (i) and equation (ii), we get,

a + b + a – b = 17 + 9

⇒ 2a = 26

$\therefore$ a = 13

Replace a with 13 in equation (i) to get the value of b.

13 + b = 17

$\therefore$ b = 17 – 13 = 4

Replace a and b with their values in 4a2 + 4b2,

4(a2 + b2)

= 4(132 + 42)

= 4(169 + 16)

= 4 × 185

= 740

Hence, the correct answer is 740.

Q2. The difference between two numbers is 9 and the difference between their squares is 207. The numbers are:

1. 17 and 8

2. 16 and 7

3. 15 and 6

4. 15 and 7

Hint: Let the numbers be $x$ and $y$. Use the formula, $(x^{2}-y^{2})=(x-y)(x+y)$

Answer:

Given: The difference between the two numbers is 9.

The difference between their squares is 207.

Let the numbers be $x$ and $y$.

Difference between the numbers $(x-y)=9$ ----------------------(1)

Difference between their squares $(x^{2}-y^{2})=207$

$⇒(x-y)(x+y)=207$ ---------------------------(2)

Substituting the value of $(x-y)$ in equation (2)

$⇒9×(x+y)=207$

$⇒(x+y)=23$ -------------------------(3)

Adding equations (1) and (3), we get,

$⇒2x=32$

$\therefore x=16$

So, $y=(23-16)=7$

Hence, the correct answer is 16 and 7.

Q3. The cost of 4 pens, 6 notebooks, and 9 files is Rs. 305. The cost of 3 pens, 4 notebooks and 2 files is Rs. 145. What is the cost (in Rs.) of 5 pens, 8 notebooks, and 16 files?

1. 515

2. 565

3. 540

4. Can not be determined

Hint: Let the cost of 1 pen, 1 notebook and 1 file be Rs. $x, y$ and $z$, respectively, then make the equations from the given information.

Answer:

Let the cost of 1 pen, 1 notebook and 1 file be Rs. $x, y$ and $z$, respectively.

The cost of 4 pens, 6 notebooks, and 9 files is Rs. 305.

The cost of 3 pens, 4 notebooks and 2 files is Rs. 145.

So, $4x + 6y+ 9z = 305$ (Equation1)

$3x + 4y + 2z = 145$ (Equation2)

Performing 2 × (Equation1) – (Equation2), we get

$5x + 8y + 16z = 2(305) - 145$

⇒ $5x + 8y + 16z = 565$

Hence, the correct answer is 565.

Q4. The product of the digits of a two-digit number is 24. If we add 45 to the number, the new number obtained is formed by interchanging the digits. What is the original number?

1. 54

2. 83

3. 38

4. 45

Hint: Take a 2-digit number with unit digit $y$ and tens digit $x$, we can write it as $10x+y$, then its reverse will be $10y+x$. Make an equation with this information and find the unknown value.

Answer:

Let the unit digit of the number be $y$ and the tens digit be $x$.

Number $= 10x$ + $y$

Product of digits $= x$ × $y = 24$ ---------------(i)

According to the question,

$10x+y+45 = 10y + x$

⇒ $9y-9x= 45$

⇒ $y-x = \frac{45}{9} = 5$ ---------------------(ii)

Solving equations (i) and (ii), we get,

$x= 3$ and $y= 8$

So, the number $=10x+y=10×3+8=38$

Hence, the correct answer is 38.

Q5. $x$ varies inversely as the square of $y$. Given that $y=2$ for $x=1$, the value of $x$ for $y=6$ will be equal to:

1. 3

2. 9

3. $\frac{1}{3}$

4. $\frac{1}{9}$

Hint: Calculate the value of the constant first. Then, insert it into the next equation.

Answer:

$x$ varies inversely as a square of $y$.

$⇒x=\frac{a}{y^2}$, where $a$ is constant

At $y=2, x=1$

$⇒1=\frac{a}{2^2}$

$⇒a=4$

If $y=6$, then,

$\therefore x=\frac{4}{6^2}=\frac{4}{36}=\frac{1}{9}$

Hence, the correct answer is $\frac{1}{9}$.

Q6. Number of solution of the two equations $4x – y = 2$ and $2y – 8x + 4 = 0$ is:

1. Zero

2. One

3. Two

4. Infinitely many

Hint: There are an infinite number of possible solutions for the equation system if two lines are in the same precise line if they share the same slope and y-intercept.

Answer:

Given: $4x - y = 2$-----(equation 1) and $2y - 8x + 4 = 0$-----(equation 2)

There are an infinite number of possible solutions for the equation system if two lines are in the same precise line if they share the same slope and y-intercept.

Rearranging equation (1) we get,

$y = 4x - 2$

Rearranging equation (2) we get,

$2y = 8x - 4$

$⇒y = 4x - 2$

From the above equation, we can see that both lines are the same.

So, there will be infinitely many solutions.

Hence, the correct answer is infinitely many.

Q7. A and B have some toffees. If A gives one toffee to B, they will have an equal number of toffees. If B gives one toffee to A, the number of toffees with A is double the number with B. The total number of toffees with A and B is:

1. 12

2. 10

3. 14

4. 15

Hint: Let the number of toffees with A and B be x and y respectively. Form linear equations to get the values of x and y.

Answer:

Let the number of toffees with A and B be x and y respectively.

According to the question:

Case 1.

x – 1 = y + 1

⇒ x = y + 2...............(equation 1)

Case 2.

x + 1 = 2(y – 1)

⇒ x – 2y = –3....................(equation 2)

Putting the value of x, we get:

2 + y – 2y = –3

⇒ y = 5

Putting the value of y in equation 1, we get:

x = 5 + 2 = 7

Total toffees = 5 + 7 = 12

Hence, the correct answer is 12.

Q8. The present age of Rahim is five times the present age of his daughter, Savita. Seven years from now, Rahim will be three times as old as Savita. What is the present age (in years) of Rahim?

1. 45 years

2. 35 years

3. 30 years

4. 40 years

Hint: Let Rahim's present age be x years and his daughter's be y years.

The two equations will be x = 5y and x + 7 = 3(y + 7).

Answer:

Let the present age of Rahim be x years and her daughter be y years.

Given: x = 5y

According to the question,

x + 7 = 3(y + 7)

⇒ x + 7 = 3y + 21

Putting the value of x, we get:

5y + 7 = 3y + 21

⇒ 2y = 14

⇒ y = 7

So, x = 5y = 5 × 7 = 35

Hence, the correct answer is 35 years.

Q9. The cost of 3 pieces of bread and 1 packet of juice at a certain store is Rs. 323.50. At the same store, the cost of 5 pieces of bread and 1 packet of juice is Rs. 433.50. What will be the cost of 2 pieces of bread and 2 packets of juice at this store?

1. Rs. 427

2. Rs. 350

3. Rs. 433

4. Rs. 403

Hint: Let the cost of one bread as $b$ and the cost of one packet of juice as $j$. Set up an equation as given information. Solve for $b$ and $j$.

Answer:

Let the cost of one bread be b and the cost of one packet of juice be j.

The cost of 3 breads and 1 packet of juice.

⇒ 3b + j = 323.50---(1)

The cost of 5 breads and 1 packet of juice.

⇒ 5b + j = 433.50---(2)

Subtracting the first equation from the second,

⇒ 2b = 433.50 - 323.50 = 110

⇒ b = $\frac{110}{2}$ = 55

Substituting b = 55 into the first equation,

⇒ 3 × 55 + j = 323.50

⇒ j = 323.50 - 165 = 158.50

So, the cost of one bread is Rs. 55 and the cost of one packet of juice is Rs. 158.50.

Therefore, the cost of 2 breads and 2 packets of juice is,

⇒ 2b + 2j = 2 × 55 + 2 × 158.50 = 110 + 317 = 427

Hence, the correct answer is Rs. 427.

Q10. The ratio of the incomes of two employees is 7 : 4, and the ratio of their expenditures is 3 : 1. If each of them manages to save INR 4800 per month, find the sum of their monthly incomes (in INR).

1. 21120

2. 20120

3. 21150

4. 18150

Hint: Let their income be $7x, 4x$ and their expenditure be $3y, y$. According to the question,

$7x-3y=4800$ ..........................(1)

$4x-y=4800$ .........................(2)

Answer:

Given: The ratio of the incomes of two employees is 7 : 4, and the ratio of their expenditures is 3 : 1. Each of them manages to save INR 4,800 per month.

Let their income be $7x, 4x$ and their expenditure be $3y, y$.

According to the question,

$7x-3y=4800$..........................(1)

$4x-y=4800$.........................(2)

Solving equations (1) and (2) we get,

$x=1920$ and $y=2880$

So, the sum of their monthly income $= (7x+4x) = 11x = 11×1920 = 21120$

Hence, the correct answer is 21120.