Lines and Angles: Definition, Calculator, Questions, Formula, Chart
Lines and Angles: An Overview
Lines and angles are fundamental concepts in geometry, essential for understanding various geometric relationships and properties. In class 9, students explore these concepts through definitions, types, and properties. The lines and angles class 9 worksheet and test paper pdf provide practical problems and examples to enhance learning. Key topics include parallel lines and vertical angles, and parallel lines and interior angles, which are often examined through diagrams and formulas. Additionally, parallel and transversal lines create alternate interiors and corresponding angles, which are vital for solving geometric questions. Tools like the parallel and transversal lines calculator can aid in visualizing and solving problems effectively.
CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts
XAT 2025: Section-wise Preparation Tips | Sample Paper
Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers
- Definition of Lines
- Definition of Angles
- Types of Lines
- Types of Angles
- Tips and Tricks
- Practice Questions
Definition of Lines
A straight one-dimensional figure that extends infinitely in both ways without any thickness or curvature is called a Line. A line does not curve or bend and can be horizontal or vertical.
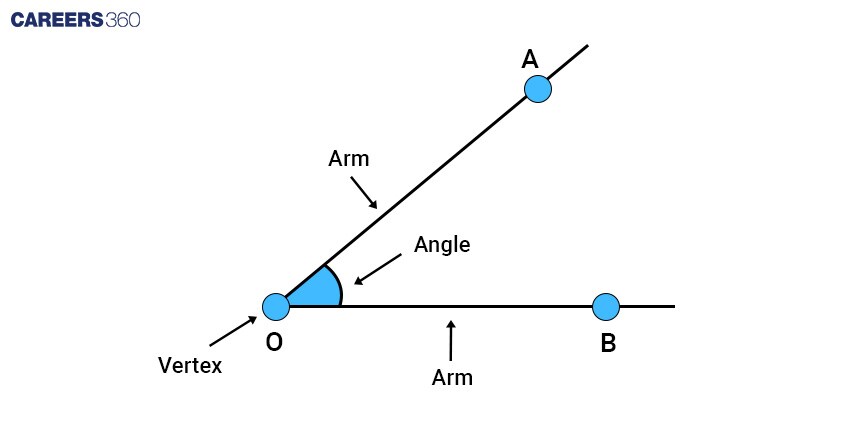
Definition of Angles
An angle is a fundamental concept in geometry that describes the figure formed by two rays or line segments sharing a common endpoint. The common endpoint is called the vertex of the angle and rays or line segments are called arms or sides of the angle. Angles measure the amount of turn or rotation between the two rays.
Types of Lines
There are several types of lines depending on the characteristics.
In the context of endpoints and length, lines are of two types.
Line segment
Ray
Lines can be classified based on their properties and relationships with other lines. Here are the types of lines:
Straight line
Horizontal line
Vertical line
Parallel line
Perpendicular line
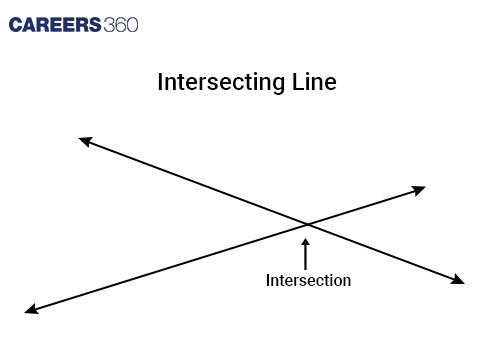
Intersecting line
Transversal line
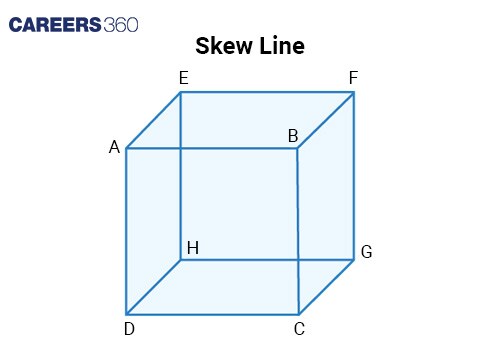
Skew line
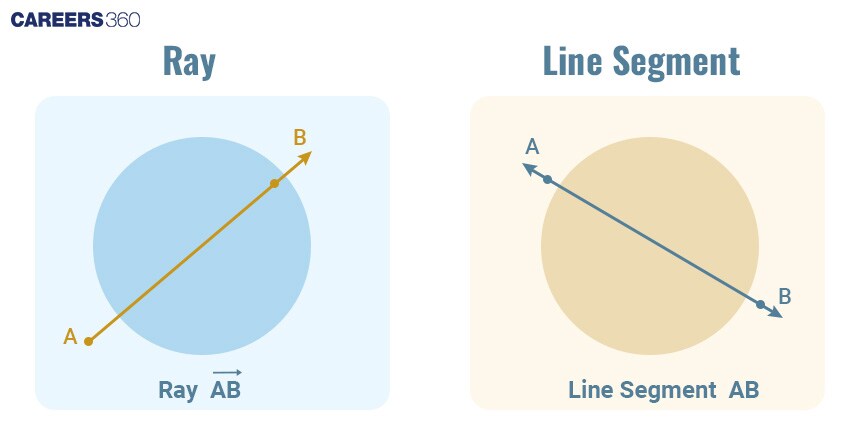
Line Segment and Ray
Ray is a type of line which has a starting point on one side but no endpoint on the other side. It continues infinitely in one end.
In the picture, A is the starting point and it crosses through point B and goes infinitely. It is denoted by Arror over AB.
A line segment is a type of line which has a starting point and endpoint. It is of finite length and does not extend beyond endpoints.
In the picture, A is the starting point or endpoint on one side and B is the endpoint or starting point on another side. It is denoted by bar AB.
Parallel lines, Perpendicular lines, Transversal lines
Types of lines | Description | Illustration |
Straight line | A line that extends infinitely on both sides and does not curve. Example: y = 2x + 3 |
|
Horizontal line | A line runs left to right and remains at a constant y-coordinate. It has a slope of zero. Example: y = 4 |
|
Vertical line | A line runs up and down and remains at a constant x-coordinate. Its slope is undefined. Example: x = -4 |
|
Parallel line | Two or more lines in a plane that never intersect because they have the same slope. Example: y = 3x + 1 |
|
Perpendicular line | When two lines intersect at a right angle (90 degrees). The slopes of perpendicular lines are negative reciprocals of each other. Example: y = -2x + 1 |
|
Intersecting line | Lines that cross at a single point. They have different slopes and meet at one point. Example: y = x + 1 |
|
Transversal line | A line which intersects two or more lines at distinct points. | |
Skew line | Skew lines exist only in three-dimensional(3D) space. Two or more lines that do not touch and also not parallel. |
|
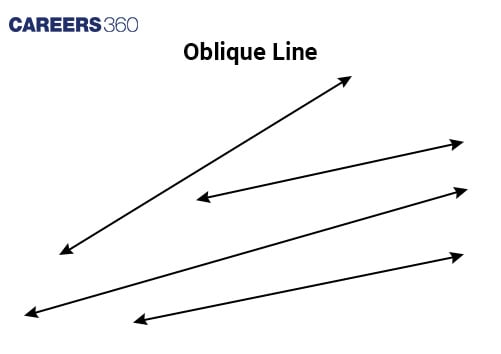
Oblique line | Lines that intersect but are not perpendicular. They have different slopes that are not negative reciprocals of each other. Example: y = x + 2 |
|
Types of Angles
There are many types of angles based on their measurement or characteristics or their position.
Types of angles based on their measurement are:
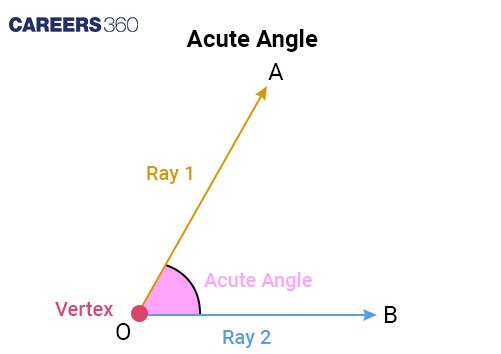
Acute angle
Right angle
Obtuse Angle
Straight Angle
Reflex Angle
Full Angle/ Complete Angle
Types of angles based on comparison with the other angle are:
Supplementary Angles
Complementary Angles
Corresponding Angles
Adjacent Angles
Vertically Opposite Angles
Alternate interior Angles
Alternate Exterior Angles
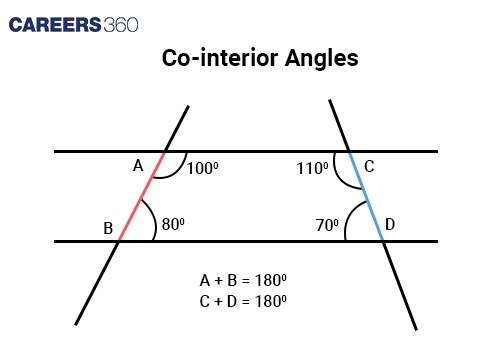
Co-interior Angles
General Classification
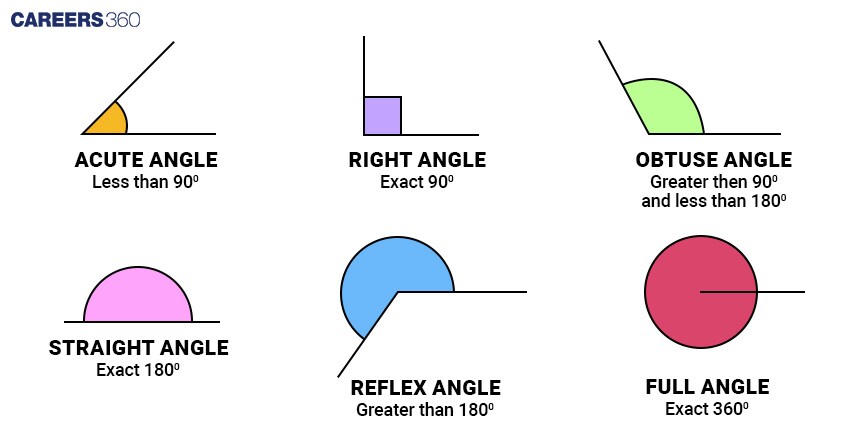
Types of angles | Description | Illustration |
Acute angle | An angle that measures less than 90°. |
|
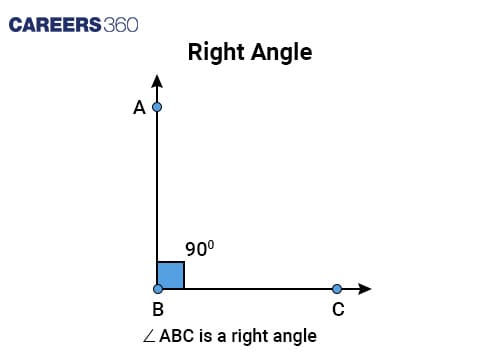
Right angle | An angle that measures exactly 90°. |
|
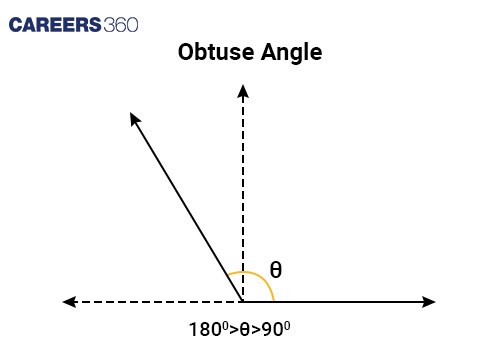
Obtuse angle | An angle that measures more than 90° but less than 180°. |
|
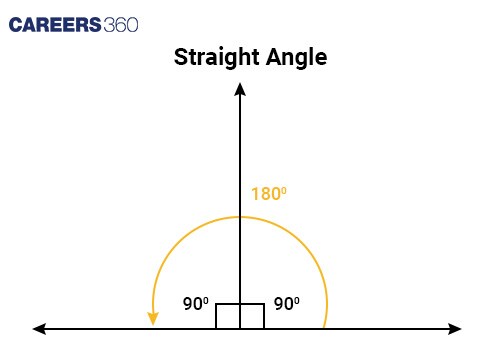
Straight angle | An angle that measures exactly 180° and is formed by a straight line. |
|
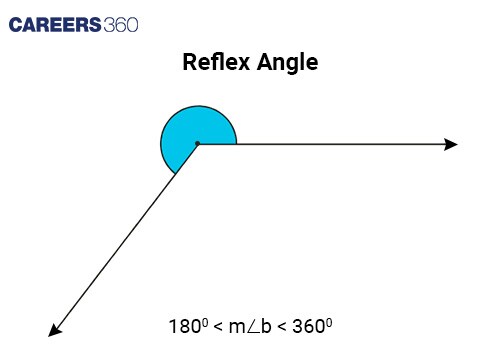
Reflex angle | An angle that measures more than 180° but less than 360°. |
|
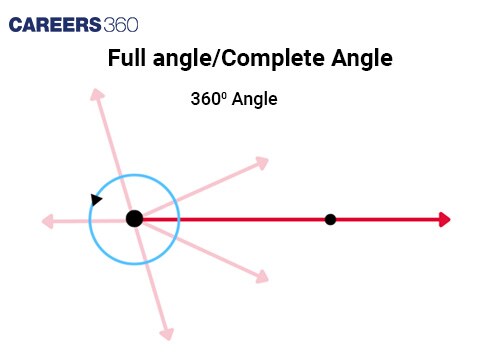
Full angle/Complete Angle | An angle that measures exactly 360°. |
|
Classification based on the relation between two angles
Types of angles | Description | Illustration |
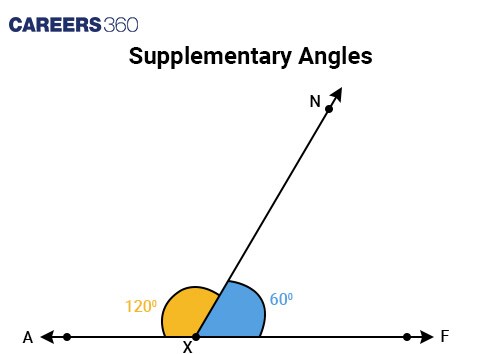
Supplementary Angles | When two angles sum up to 180°. Example: Angles AXN and FXN sum up to 180°.(120° + 60°) So, Angles AXN and FXN are supplementary angles. |
|
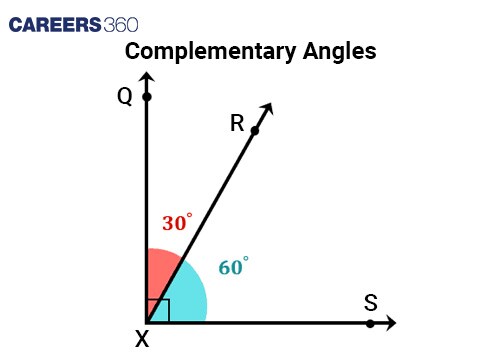
Complementary Angles | When two angles sum up to 90°. Example: Angles RXQ and RXS sum up to 90°.(30° + 60°) |
|
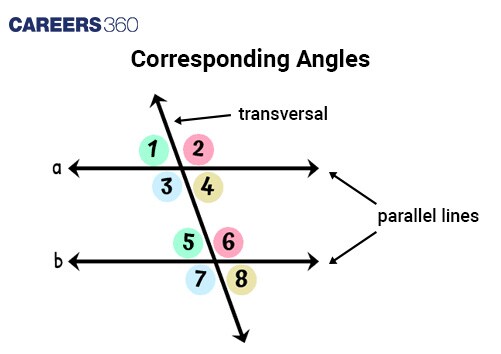
Corresponding Angles | Angles that are in the same relative position at each intersection of a transversal with two parallel lines. Corresponding angles between two parallel lines are always equal and vice versa. Example: Angle 2 and 6 are equal. Angle 1 and 5 are equal. Angle 4 and 8 are equal. Angle 3 and 7 are equal. |
|
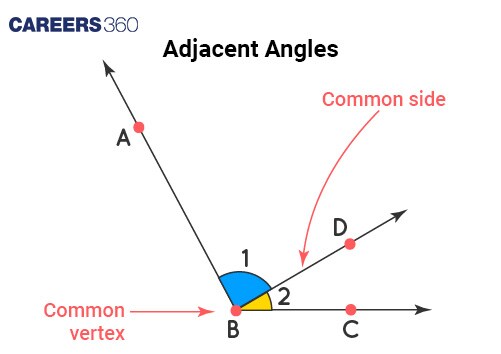
Adjacent Angles | When two angles share a common vertex and a common side but do not overlap. Example: Angles ABC and DBC where B is the common vertex. |
|
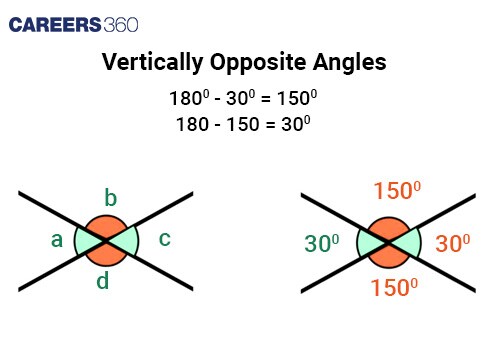
Vertically Opposite angles | If two lines intersect, the angles opposite each other at the intersection are vertically opposite. Vertically opposite angles are equal. Example: Angle a = Angle c and Angle b = Angle d |
|
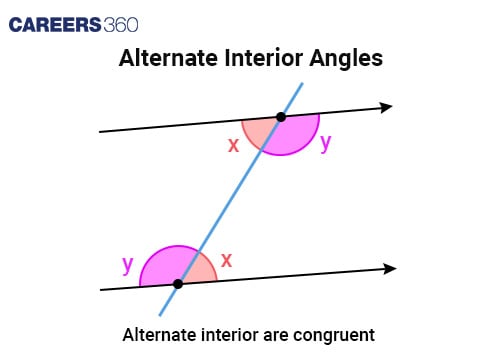
Alternate interior angles | Angles on opposite sides of a transversal but inside the two lines. Alternate interior angles between two parallel lines are always equal and vice versa. |
|
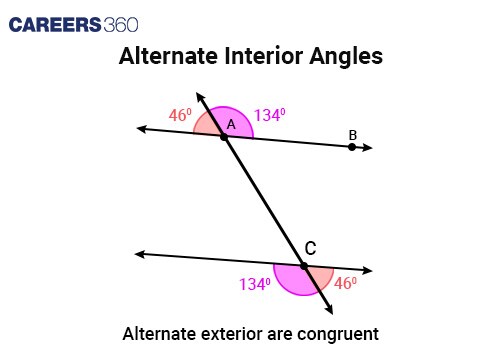
Alternate Exterior angles | Angles on opposite sides of a transversal but outside the two lines. Alternate exterior angles between two parallel lines are always equal and vice versa. |
|
Co-interior angles | Pairs of angles that are on the same side of a transversal cutting through two parallel lines. These angles lie between the two parallel lines. Sum of co-interior angles between two parallel lines is 180 degree. |
|
Tips and Tricks
If one angle is given, then subtract it from 180° to get its supplementary angle.
If one angle is given, then subtract it from 90° to get its complementary angle.
In vertical angles, opposite angles formed by two intersecting lines are equal.
Angles on opposite sides of the transversal but inside the two lines are equal.
Angles on opposite sides of the transversal but outside the two lines are equal.
If two lines are perpendicular, they form four right angles at their intersection.
Co-interior angles lie between the two parallel lines on the same side of the transversal line.
Practice Questions
Q1. If the sum and difference of two angles are 135° and $\frac{\pi}{12}$, respectively, then the value of the angles in degree measure is:
70° and 65°
75° and 60°
45° and 90°
80° and 55°
Hint: Use ${\pi}=180°$ and form linear equations.
Answer:
Let the two angles be x and y.
So, x + y = 135°------------------------------(1)
The difference of the two angles is $\frac{\pi}{12}$.
So, x – y = $\frac{\pi}{12}=\frac{180}{12}$ = 15° ---------------------------(2)
Solving equations (1) and (2), we get,
x = 75°
So, y = 135 – 75 = 60°
Hence, the correct answer is 75° and 60°.
Q2. In an isosceles triangle, if the unequal angle is 4 times the sum of the equal angles, then each equal angle is:
25°
30°
21°
18°
Hint: Use and set up an equation as given as the unequal angle is 4 times the sum of the equal angles and the angle sum property of a triangle.
Answer:
In an isosceles triangle, two angles are equal.
Let the equal angles be $\angle B$ and $\angle C$ ($\angle B=\angle C$). The third angle which is unequal is $\angle A$.
Given that the unequal angle is $4$ times the sum of the equal angles.
$=4(\angle B+\angle C)$
$=4(\angle B+\angle B)$
$=4(2\angle B)$
$=8\angle B$
The sum of the angles in a triangle is always $180^{\circ}$.
$\Rightarrow 2\angle B+ 8\angle B = 180^{\circ}$
$\Rightarrow 10\angle B = 180^{\circ}$
$\Rightarrow \angle B= 18^{\circ}$
Hence, the correct answer is $18^{\circ}$.
Q3. In $\triangle \mathrm{ABC}$, $\angle \mathrm{ABC} = 90^{\circ}$, $\mathrm{BP}$ is drawn perpendicular to $\mathrm{AC}$. If $\angle \mathrm{BAP} = 50^{\circ},$ what is the value of $\angle \mathrm{PBC}?$
30°
45°
50°
60°
Hint: Use the angle sum property and complementary angles to find $\angle \mathrm{PBC}$.
Answer:
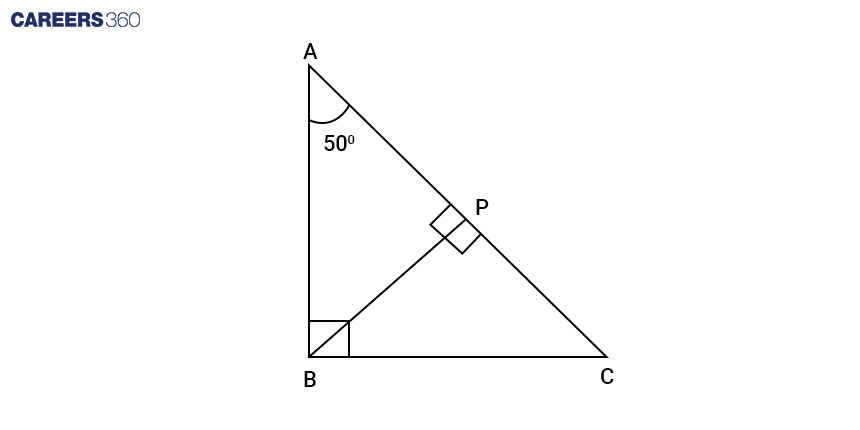
In right-angled $\triangle \mathrm{ABC}$, where $\angle \mathrm{ABC} = 90^{\circ}$, $\mathrm{BP}$ is drawn perpendicular to $\mathrm{AC}$. Given that $\angle \mathrm{BAP }= 50^{\circ}$
In $\triangle\mathrm{ ABC}$,
$\mathrm{\angle C = 180^{\circ} - \angle A - \angle B = 180^{\circ} - 50^{\circ} - 90^{\circ} = 40^{\circ}}$
In $\mathrm{\triangle BPC}$,
$\mathrm{\angle PBC +\angle BPC +\angle PCB =180^{\circ}}$
⇒ $\mathrm{\angle PBC = 90^{\circ} - \angle PCB = 90^{\circ} - 40^{\circ} = 50^{\circ}}$
Hence, the correct answer is $50^{\circ}$.
Q4. ABC is an isosceles triangle having AB = AC and $\angle$A = 40$^\circ$. Bisector PO and OQ of the exterior angle $\angle$ ABD and $\angle$ ACE formed by producing BC on both sides, meet at O, then the value of $\angle$BOC is:
70°
110°
80°
55°
Hint: Use the angle sum property and the concept of vertically opposite angles to solve this.
Answer:
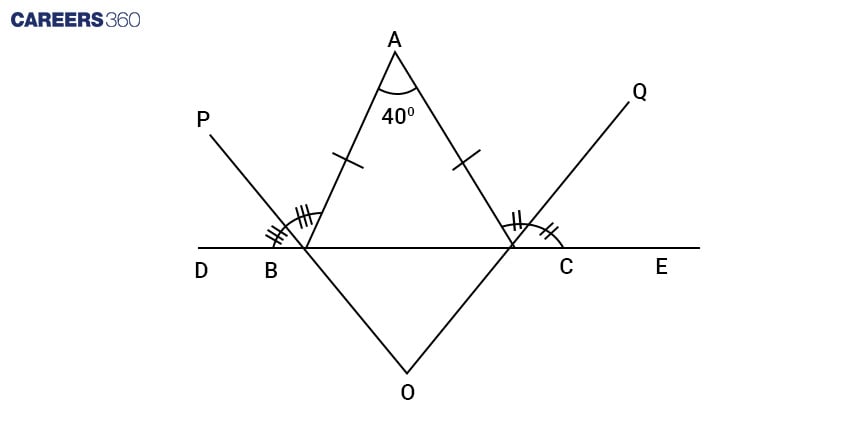
Given, an isosceles $\triangle$ ABC with AB = BC
And, $\angle$ A = 40$^\circ$ with bisectors PO and OQ of $\angle$ ABD and $\angle$ ACE.
In $\triangle$ ABC,
$\angle$A + $\angle$ B+ $\angle$ C = 180$^\circ$
Or, 40$^\circ$ + 2$\angle$C = 180$^\circ$
Or, $\angle$ B = $\angle$ C = 70$^\circ$
Now, $\angle$ ABD + $\angle$ ABC = 180$^\circ$
Or, $\angle$ ABD + 70$^\circ$ = 180$^\circ$
Or, $\angle$ ABD = 110$^\circ$
Since PO is an angle bisector, $\angle$ PBD = $\frac{110^\circ}{2}=55^\circ$
Similarly, $\angle$ QCE = 55$^\circ$
In $\triangle$ BCO,
$\angle$BOC + $\angle$ CBO+ $\angle$ BCO = 180$^\circ$
Or, $\angle$ BOC + $\angle$ PBD+ $\angle$ QCE = 180$^\circ$ (vertically opposite angles)
Or, $\angle$ BOC + 55$^\circ$ + 55$^\circ$ = 180$^\circ$
Or, $\angle$ BOC = 70$^\circ$
Hence, the correct answer is 70$^\circ$.
Q5. In the following figure, if l || m, then find the measures of angles marked by a and b.
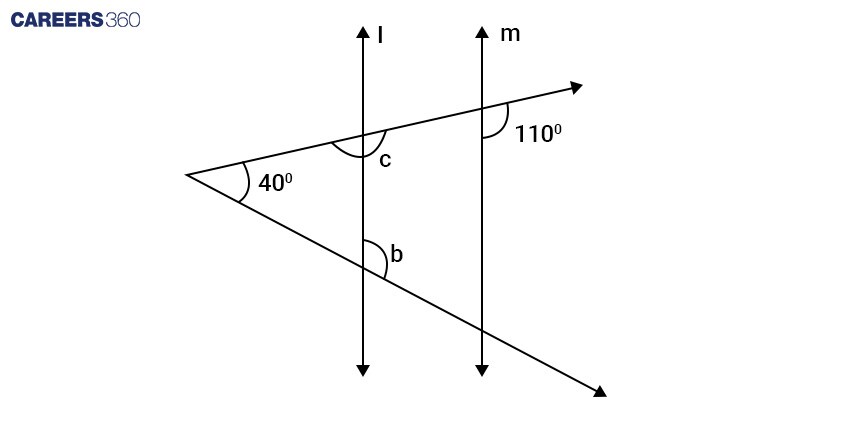
a = 90$^{\circ}$ and b = 90$^{\circ}$
a = 55$^{\circ}$ and b = 125$^{\circ}$
a = 70$^{\circ}$ and b = 110$^{\circ}$
a = 60$^{\circ}$ and b = 120$^{\circ}$
Hint: For two parallel lines, the corresponding angles are equal.
A triangle's exterior angle equals the sum of opposite interior angles.
Answer:
Since $l \parallel m$,
⇒ $\angle$ c = 110$^{\circ}$ (corresponding angles are equal)
Also, $\angle$ a + $\angle$ c = 180$^{\circ}$ (supplementary angles)
⇒ $\angle$ a = 180$^{\circ}$ – 110$^{\circ}$ = 70$^{\circ}$
Now, $\angle$ b = $\angle$ a + 40$^{\circ}$ (exterior angle of a triangle)
= 70$^{\circ}$ + 40$^{\circ}$
= 110$^{\circ}$
Hence, the correct answer is a = 70$^{\circ}$ and b = 110$^{\circ}$.
Q6. An angle is greater than its complementary angle by 30°. Find the measure of the angle.
30°
90°
60°
120°
Hint: Let $x$ be the angle and the complement of the angle be $(90°-x)$.
Answer:
Let $x$ be the angle and the complement of the angle be $(90°-x)$.
According to the question,
$(90°-x)+30°=x$
⇒ $2x=120°$
$\therefore x =60°$
Hence, the correct angle is 60°.
Q7. An angle $\frac{1}{3}$rd of its supplementary angle. Find the measure of the angle.
45°
90°
135°
22.5°
Hint: Let $x$ be the angle.
The supplement of the angle is $(180°-x)$.
Answer:
Let $x$ be the angle.
The supplement of the angle is $(180°-x)$.
According to the question,
$\frac{1}{3}(180°-x)=x$
⇒ $180°-x=3x$
⇒ $4x=180°$
$\therefore x =45°$
Hence, the correct answer is 45°.
Frequently Asked Questions (FAQs)
A straight one-dimensional figure that extends infinitely in both ways without any thickness or curvature is called a Line. A line does not curve or bend and can be horizontal or vertical.
An angle is a fundamental concept in geometry that describes the figure formed by two rays or line segments sharing a common endpoint. The common endpoint is called the vertex of the angle and rays or line segments are called arms or sides of the angle. Angles measure the amount of turn or rotation between the two rays.
There 6 main types of angles.
These are:
Acute angle
Right angle
Obtuse Angle
Straight Angle
Reflex Angle
Full Angle
An angle that measures less than 90° is called an acute angle.
Example: 75° is an acute angle as it measures less than 90°.
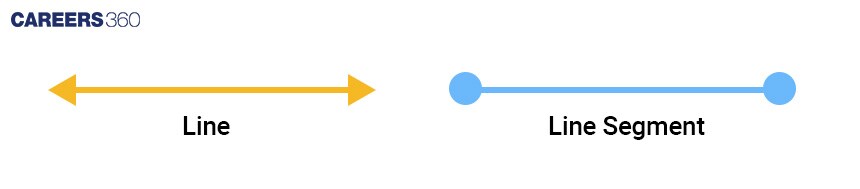
Line | Line segment | |
Definition | A line is a straight one-dimensional figure that extends infinitely in both directions. | A line segment is a part of a line that has two distinct endpoints. |
Length | Infinite | Finite |
Endpoints | Only starting point. No endpoints | Endpoints on both sides. |
Measurable or not | It is not measurable. | It is measurable. |
Ray is a type of line that has a starting point on one side but no endpoint on the other side. It continues infinitely in one end.
A line segment is a type of line that has a starting point and endpoint. It is of finite length and does not extend beyond endpoints.