Parallelogram and Mid Point Theorem: Definition, Formula, Properties

Parallelogram and Mid point theorem are one of the most important topics in geometry. Many theorems are related to parallelograms and one such theorem is mid point theorem. In this article, we have to discuss parallelogram theorems, parallelogram diagonals theorem, parallelogram theorems in geometry, parallelogram theorems worksheet, parallelogram theorems calculator, parallelogram theorems properties, mid point theorem formula, mid point theorem proof, mid point theorem explanation etc.

We have also stated and proved the midpoint theorem and some of the theorems related to quadrilateral properties. We have also compared quadrilaterals with four-sided polygons like rectangle, square, rhombus, and trapezium.

Parallelogram: A general description

A parallelogram is a four-sided quadrilateral or polygon with distinctive properties from other quadrilaterals.

In a parallelogram:

• Opposite sides are equal.

• Opposite sides are parallel to each other.

• Opposite angles are equal.

• Diagonals bisect each other.

• Adjacent angles sum up to 180°.

Sides and Angles of a parallelogram

• Opposite sides: In a parallelogram, the opposite sides are equal in length and parallel.

If ABCD is a parallelogram with sides AB, BC, CD, and DA, then AB = CD, BC = DA, AB || CD, and BC || DA.

• Opposite angles: opposite angles of a parallelogram are equal.

In a parallelogram ABCD, ∠A = ∠C and ∠B = ∠D

• Consecutive angles: Consecutive angles in a parallelogram are supplementary. That means the sum of those angles is 180°.

In a parallelogram ABCD, ∠A + ∠C = 180°, ∠B + ∠C = 180°, ∠C + ∠D = 180° and ∠D + ∠A = 180°

• Diagonals: Diagonals of a parallelogram bisect each other. One diagonal of a parallelogram divides the parallelogram into two congruent triangles.

In a parallelogram ABCD, AC and BD are diagonals. AC divides ABCD into two congruent triangles ABC and ADC, BD divides ABCD into two congruent triangles ABD and BDC.

If E is the intersection of two diagonals AC and BD, then AE = CE and BE = DE

Parallelogram and other quadrilateral

Is Trapezium a parallelogram?

Trapezium is not a parallelogram. Because Trapezium and Parallelogram have different properties.

In a parallelogram,

• Opposite sides are equal.

• The opposite sides are parallel.

• Opposite angles are equal.

But in a Trapezium,

• Only one pair of parallel sides, which are called the bases of the Trapezium.

• The other pair of sides are not parallel and can differ in length. They are called the legs of a Trapezium.

Is Square a parallelogram?

A square is a parallelogram. Because the properties of square and parallelogram match.

The common properties between squares and parallelograms are:

• Opposite sides are equal.

• Opposite sides are parallel.

• Opposite angles are equal.

• Adjacent angles are supplementary.

• Diagonals bisect each other.

In addition to that, squares have some extra properties.

• All four sides are equal.

• All four angles are right angles.

• Diagonals are equal.

• Diagonals bisect each other at right angles.

Therefore, while all squares are parallelograms, not all parallelograms are squares.

Is a Rectangle a parallelogram?

A rectangle is a parallelogram. Because the properties of rectangle and parallelogram match.

The common properties between rectangles and parallelograms are:

• Opposite sides are equal.

• Opposite sides are parallel.

• Opposite angles are equal.

• Adjacent angles are supplementary.

• Diagonals bisect each other.

In addition, rectangles have some extra properties.

• All the angles of a rectangle are right angles.

• Diagonals are equal in length.

Therefore, while all rectangles are parallelograms, not all parallelograms are rectangles.

Is Rhombus a parallelogram?

A rhombus is a parallelogram. Because the properties of rhombus and parallelogram match.

The common properties between rhombuses and parallelograms are:

• Opposite sides are equal.

• The opposite sides are parallel.

• Opposite angles are equal.

• Adjacent angles are supplementary.

• Diagonals bisect each other.

In addition to that, rhombuses have some extra properties.

• All four sides are equal.

• Diagonals bisect each other at right angles.

• Diagonals bisect the angles of the rhombus.

Therefore, while all rhombuses are parallelograms, not all parallelograms are rhombuses.

Difference between parallelogram, Rhombus, Square, Rectangle, and Trapezium

The perimeter of a parallelogram

The perimeter of a parallelogram is the total distance around the parallelogram. It is calculated by adding the lengths of all four sides.

If ABCD is a parallelogram with sides a, b, c, and d,

Then Perimeter of parallelogram ABCD = a + b + c + d

As we know, in a parallelogram, opposite sides are equal.

So a = c, b = d

We can now write it like

Perimeter of parallelogram ABCD = 2a + 2b = 2(a + b)

If one side and the lengths of diagonals are known,

The perimeter of the parallelogram = 2a + √(2x2 + 2y2 – 4a2), where x and y are the lengths of diagonals and a is the length of the side.

If one side and height along with one of the angles is known,

The perimeter of a parallelogram = 2a + (2h/sinθ), where a is the length of the side, h is the height of the parallelogram, and θ is the given angle.

Area of a parallelogram

The area of a parallelogram can be calculated by multiplying its base and height.

So, the Area of a parallelogram = Base × Its corresponding height

Alternatively, if the lengths of two adjacent sides and the included angle are known, then

The area of a parallelogram = a b sinθ, where a and b are the lengths of the sides, and θ is the included angle.

Theorems of parallelogram

Parallelograms have many important theorems. We have given the statements of the theorems and proved them below.

Theorem 1: Parallelograms on the same base and between the same parallel sides are equal in area.

Statement: Parallelograms that share the same base and are situated between the same parallel lines have equal areas.

Proof:

Here ABCD and EBCF are two parallelograms with the same base BC and are between the same parallel lines AD || BC, EF || BC.

We have to prove that the area of ABCD = The area of EBCF.

Let’s draw two perpendicular lines from points A and E on line BC, meeting the line BC on points M and N respectively.

So, AM and EN are perpendicular distances of A and E to BC, respectively.

We know, the Area of a parallelogram = Base × Its corresponding height

So, the area of parallelogram ABCD = BC × AM

The area of parallelogram EBCF = BC × EN

As AD and EF are both parallel to BC, any distance between AD to BC and EF to BC will be equal.

Therefore AM = EN

Now, the area of parallelogram ABCD = BC × AM = BC × EN [As AM = EN]

Hence, the area of ABCD = the area of EBCF

This proves that Parallelograms that share the same base and are situated between the same parallel lines have equal areas.

Theorem 2: The area of a parallelogram is equal to the product of its base and the corresponding altitude.

Statement: The area of a parallelogram is equal to the product of its base and the corresponding altitude (height).

Proof:

ABCD is a parallelogram with base AB.

Let BL be the perpendicular distance from AB to CD.

We have to prove the area of the parallelogram ABCD = AB × BL

Draw a perpendicular from point A which meets the extended CD at point M.

ABLM is a rectangle.

Both rectangle ABLM and parallelogram ABCD have base AB.

So, their area will be the same.

We know, the area of a rectangle = Length × Breadth

So, the area of rectangle ABLM = AB × BL = the area of parallelogram ABCD

Hence, the area of the parallelogram ABCD = AB × BL

This proves that the area of a parallelogram is equal to the product of its base and the corresponding altitude (height).

Midpoint Theorem

Statement: The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of the length of the third side.

Proof of Midpoint Theorem

In ΔABC, D and E are the midpoints of sides AB and AC, respectively.

We have to prove that, DE || BC and DE = $\frac{1}{2}$ × BC

In ΔABC, through C, draw a line parallel to BA, and it meets extend DE at point F.

In ΔAED and ΔCEF,

∠DAE = ∠ECF (alternate interior angles)

AE = EC (E is the midpoint of AC)

∠AED = ∠CEF (vertically opposite angles)

Therefore, by ASA(Angle-Side-Angle) rule, ΔAED ≅ ΔCEF

So, DE = EF and AD = CF (Corresponding parts of congruent triangles are congruent)

Now, AD = BD

⇒ BD = CF

So, BCFD is a parallelogram. (Since BD || CF and BD = CF)

⇒ DF || BC and DF = BC

Therefore, DE || BC ……….(1)

Also, DE + EF = BC

⇒ 2DE = BC

⇒ DE = $\frac{1}{2}$ × BC ………….(2)

From (1) and (2), we get,

DE || BC and DE = $\frac{1}{2}$ × BC

This proves that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of the length of the third side.

Example:

In a $\triangle$ ABC, AB = BC, and P, Q, and R are the midpoints of the sides AB, BC, and AC, respectively. If PR = 5 cm, then find the length of QR.

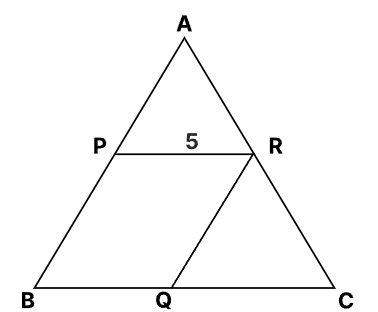
According to the question,

PR = 5 cm

Then, BC = 2 × PR = 10 cm

[The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.]

In $\triangle$ABC, if AB = BC then,

AB = 10 cm

From the mid-point theorem,

QR = $\frac{\text{AB}}{2} = \frac{10}{2} = 5$ cm

Hence, the correct answer is 5 cm.

Converse of Midpoint Theorem

Statement: If a line segment drawn through the midpoint of one side of a triangle is parallel to another side of the triangle, then it bisects the third side.

Proof of Converse of Midpoint Theorem

In ΔABC, D is the midpoint of AB and DE || BC.

We have to prove E is the midpoint of AC.

In ΔABC, through C, draw a line parallel to BA, and it meets extend DE at point F.

Here BD is parallel to CF. [By construction]

Also DF || BC

So, BCFD is a paralleogram.

BD = CF [Opposite sides of parallelograms are equal]

Also AD = BD [D is the midpoint of AB]

So, AD = CF

In ΔAED and ΔCEF,

∠DAE = ∠ECF [alternate interior angles]

AD = CF [Proved above]

∠AED = ∠CEF [vertically opposite angles]

Therefore, by ASA(Angle-Side-Angle) rule, ΔAED ≅ ΔCEF

So, AE = CE (Corresponding sides of congruent triangles)

Hence, E is the midpoint of AC.

This proves that if a line segment drawn through the midpoint of one side of a triangle is parallel to another side of the triangle, then it bisects the third side.

Important points

• Area of a parallelogram = Length of a side × Its corresponding height

• The midpoint theorem states that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of the length of the third side.

• If a line segment drawn through the midpoint of one side of a triangle is parallel to another side of the triangle, then it bisects the third side.

• Parallelograms that share the same base and are situated between the same parallel lines have equal areas.

• Perimeter of parallelogram ABCD with sides a, b, c, and d = 2a + 2b = 2(a + b)

• Squares, rectangles, and rhombuses are parallelograms but Trapeziums are not parallelograms.

Practice Questions

Q1. The area of the parallelogram whose length is 30 cm, width is 20 cm and diagonal is 40 cm is:

1. $200\sqrt{15}\text{ cm}^{2}$

2. $100\sqrt{15}\text{ cm}^{2}$

3. $300\sqrt{15}\text{ cm}^{2}$

4. $150\sqrt{15}\text{ cm}^{2}$

Hint: Area of triangle = $\sqrt{s(s - a)(s - b)(s - c)}$ where $s$ is semi-perimeter and $a, b, c$ are sides of the triangle.

Answer: D

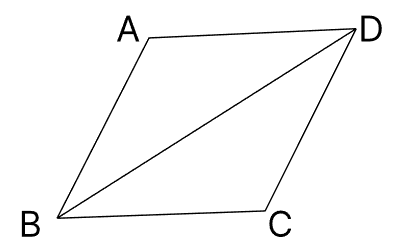
In $\triangle$ ABD,

AB = 20 cm. AD = 30 cm. BD = 40 cm

Semi perimeter (s) = $\frac{a+b+c}{2}$ = $\frac{20+30+40}{2}$ = 45 cm

Now, the area of $\triangle$ABD

= $\sqrt{s(s - a)(s - b)(s - c)}$

= $\sqrt{45(45 - 20)(45 - 30)(45 - 40)}$

= $\sqrt{45 \times 25 \times 15 \times 5}$

= $\sqrt{5 \times 3 \times 5 \times 5 \times 5 \times 3 \times 5}$

= $\sqrt{5^2 \times 5^2 \times 5 \times 3^2 \times 3}$

= $5 \times 5 \times 3\sqrt{15}$

= $75\sqrt{15}$

$\therefore$ Area of parallelogram ABCD $=2 \times 75\sqrt{15}=150\sqrt{15}\text{ cm}^2$

Hence, the correct answer is $150\sqrt{15}\text{ cm}^2$.

Q2. Two sides of a parallelogram are 20 cm and 25 cm. If the altitude corresponding to the side of the length 25 cm is 10 cm, then the altitude corresponding to the other pair of sides is:

1. 10 cm

2. 10.5 cm

3. 12 cm

4. 12.5 cm

Hint: Area of a parallelogram = Length of a side × Its corresponding height

Answer: D

Given: Two sides of a parallelogram are 20 cm and 25 cm. If the altitude corresponding to the side of length 25 cm is 10 cm.

Let the altitude corresponding to the other pair of sides be $h$ cm.

According to the question,

20 × $h$ = 25 × 10

⇒ $h$ = $\frac{25×10}{20}$

$\therefore h$ = $\frac{25}{2}$ = 12.5 cm

Hence, the correct answer is 12.5 cm.

Q3. A triangle and a parallelogram have the same base 28 cm and the same area. If the height of the parallelogram is 12 cm, then find the length of the altitude of the triangle.

1. 28 cm

2. 23 cm

3. 24 cm

4. 21 cm

Hint: Area of a parallelogram = Base $\times$ Height

Area of a triangle = $\frac{1}{2}\times$ Height $\times$ Base

Answer: C

Area of the parallelogram = $28 \times 12 = 336\ \mathrm{cm^2}$

Let the length of the altitude of the triangle be $h$ cm.

According to the question,

$\frac{1}{2}\times h \times 28 = 336$

⇒ $h = 12\times2$

⇒ $h = 24\text{ cm}$

Hence, the correct answer is 24 cm.

Q4. A field is 150 m long and 80 m wide. How many times (rounded off to 1 decimal place) is its perimeter to the length of its diagonal?

1. 2.3

2. 2.5

3. 2.7

4. 3.1

Hint: Length of the diagonal = $\sqrt{(l^2+w^2)}$, where $l$ = length, $w$ = width

Answer: C

Length $(l)$ = 150 m

Width $(w)$ = 80 m

Perimeter $=2(l+b)=2(150+80) = 460$ m

Length of diagonal = $\sqrt{(l^2+w^2)} = \sqrt{(150^2+80^2)} =170$ m

Ratio of perimeter to diagonal $=\frac{460}{170} = 2.7$

Hence, the correct answer is 2.7.

Q5. M is the mid-point of side QR of a parallelogram PQRS (P being on the top left hand, followed by other points going clockwise). The line SM is drawn intersecting PQ produced at I. What is the length (in terms of the length of SR) of PI?

1. $\frac{3 \mathrm{SR}}{2}$

2. $\frac{\mathrm{SR}}{2}$

3. $2 \mathrm{SR}$

4. $\mathrm{SR}$

Hint: The midpoint theorem states that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of the length of the third side. Use this information to solve the question.

Answer: C

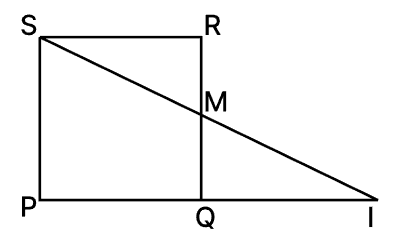
In $\triangle$PIS, M is the midpoint of QR and QM || PS

$\therefore$ Q is the midpoint of PI [converse of mid-point theorem]

⇒ PI = 2PQ

Given, PQRS is a parallelogram.

Since, in parallelogram opposite sides are parallel and equal.

Therefore, PQ = SR

⇒ PI = 2SR

Hence, the correct answer is $2 \mathrm{SR}$.

Q6. The two adjacent sides of a parallelogram are 12 cm and 5 cm respectively. If one of the diagonals is 13 cm long, then what is the area of the parallelogram?

1. 60 cm2

2. 30 cm2

3. 75 cm2

4. 25 cm2

Hint: Find the area of one of the triangles using the formula:

$\sqrt{s(s-a)(s-b)(s-c)}$, where $s$ is the semiperimeter and $a,b,c$ are the sides of the triangle.

Answer: A

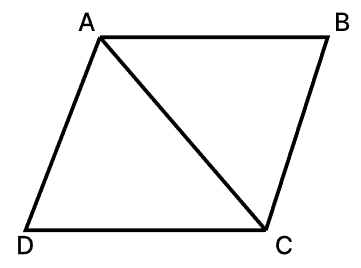
In $\triangle$ABC, AB = 12 cm, BC = 5 cm and AC = 13 cm

The semiperimeter ($s$) = $\frac{12+5+13}{2}$ = 15 cm

So, the area of $\triangle$ABC

= $\sqrt{15(15-13)(15-12)(15-5)}$

= $\sqrt{15×2×3×10}$

= 30 cm2

Now, the area of the parallelogram ABCD = 2 × the area of $\triangle$ABC = 2 × 30 = 60 cm2

Hence, the correct answer is 60 cm2.

Q7. The midpoints of AB and AC of a $\triangle$ABC are X and Y, respectively. If BC + XY = 24 units, then the value of BC − XY is:

1. 5 cm

2. 4 cm

3. 6 cm

4. 8 cm

Hint: The line segment in a triangle joining the midpoint of any two sides of the triangle is said to be parallel to its third side and half the length of the third side.

Answer: D

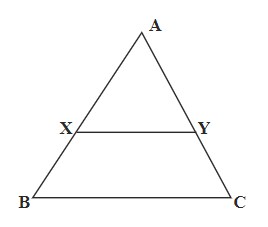
The line segment in a triangle joining the midpoint of any two sides of the triangle is said to be parallel to its third side and half the length of the third side.

According to the question,

BC + XY = 24 ..........(1)

Since XY = $\frac{1}{2}$ of BC,

⇒ $\frac{1}{2}$BC + BC = 24

⇒ 3BC = 24 × 2

⇒ 3BC = 48

⇒ BC = 16 cm

From Eq. (1) we get,

⇒ 16 + XY = 24

⇒ XY = 8 cm

Now accordingly,

⇒ BC – XY = 16 – 8 = 8 cm

The value of BC – XY is 8 cm.

Hence, the correct answer is 8 cm.

Q8. PQRA is a rectangle, AP = 22 cm and PQ = 8 cm. $\triangle$ABC is a triangle whose vertices lie on the sides of PQRA such that BQ = 2 cm and QC = 16 cm. Then the length of the line joining the midpoints of the sides AB and BC is:

1. $4\sqrt2$ cm

2. 5 cm

3. 6 cm

4. 10 cm

Hint: From $\triangle$ACR find AC, then try to find DE. Use the Pythagoras theorem:

(Hypotenuse)2 = (Base)2 + (Perpendicular)2

Answer: B

Given: PQRA is a rectangle, AP = 22 cm and PQ = 8 cm. $\triangle$ABC is a triangle whose vertices lie on the sides of PQRA such that BQ = 2 cm and QC = 16 cm.

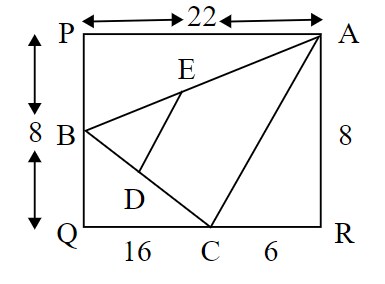
Let D and E be the two midpoints of BC and AB, respectively.

PQRA is a rectangle, PA = QR = 22 cm, PQ = AR = 8 cm and QC = 16 cm.

So, CR = (22 – 16) = 6 cm

From $\triangle$ACR,

AC = $\sqrt{8^2+6^2}$

⇒ AC = 10 cm

Since D and E are the two midpoints of BC and AB, respectively,

So, DE = $\frac{AC}{2}$

⇒ DE = $\frac{10}{2}$

⇒ DE = 5 cm

Hence, the correct answer is 5 cm.

Frequently Asked Questions

Q1. What is a parallelogram?

Answer:

A parallelogram is a four-sided quadrilateral with distinctive properties from other quadrilaterals.

In a parallelogram:

• Opposite sides are equal.

• Opposite sides are parallel to each other.

• Opposite angles are equal.

• Diagonals bisect each other.

• Adjacent angles sum up to 180°.

Q2. What does the Midpoint theorem state?

Answer:

The Midpoint theorem states that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of the length of the third side.

Q3. What are the types of parallelograms?

Answer:

There are three special types of parallelograms.

• Rectangles: Opposite sides of rectangles are equal and each interior angle is 90°.

• Rhombuses: All four sides of rhombuses are equal and opposite sides are parallel to each other.

• Squares: Squares have four equal sides and each interior angle is 90°.

Q4. Is trapezium a parallelogram?

Answer:

Trapezium is not a parallelogram. Because Trapezium and Parallelogram have different properties.

In a parallelogram,

• Opposite sides are equal.

• The opposite sides are parallel.

• Opposite angles are equal.

But in a Trapezium,

• Only one pair of parallel sides, which are called the bases of the Trapezium.

• The other pair of sides are not parallel and can differ in length. They are called the legs of a Trapezium.

Q5. When are the Midpoint theorem and converse of the Midpoint theorem used?

Answer:

• The Midpoint Theorem is often used in proving properties related to parallel lines and similar triangles.

• The converse of the Midpoint Theorem is useful in proving that a given point is the midpoint of a side of a triangle.

• Midpoint theorem is useful in constructing geometric shapes and figures, especially when dealing with parallel lines and midpoints.

• In various geometry problems, the Midpoint Theorem is used to determine unknown side lengths and angles by introducing midpoints and parallel lines.