Perfect squares and perfect Cubes

Perfect squares and perfect Cubes are fundamental parts of mathematics, with their distinct properties and wide applications across various fields. They are integral parts of both basic arithmetic and more advanced mathematical concepts. Understanding the properties and applications of Perfect Squares and Perfect Cubes can greatly enhance problem-solving skills and mathematical comprehension.
In this article, we are going to discuss Perfect Squares and Perfect Cubes, Perfect Squares and Perfect Cubes List, the difference between Perfect Squares and Perfect Cubes, and Perfect Squares and Perfect Cubes examples.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

Perfect Squares and Perfect Cubes List

Here are some examples of Perfect square numbers:

• 100 = 10²

• 225 = 15²

• 625 = 25²

• 900 = 30²

Here are some examples of Perfect cube numbers:

• 64 = 4³

• 125 = 5³

• 729 = 9³

• 1000 = 10³

A list of a few perfect squares and perfect cubes is given below:

Usage of perfect square and perfect cubes numbers

Perfect Squares

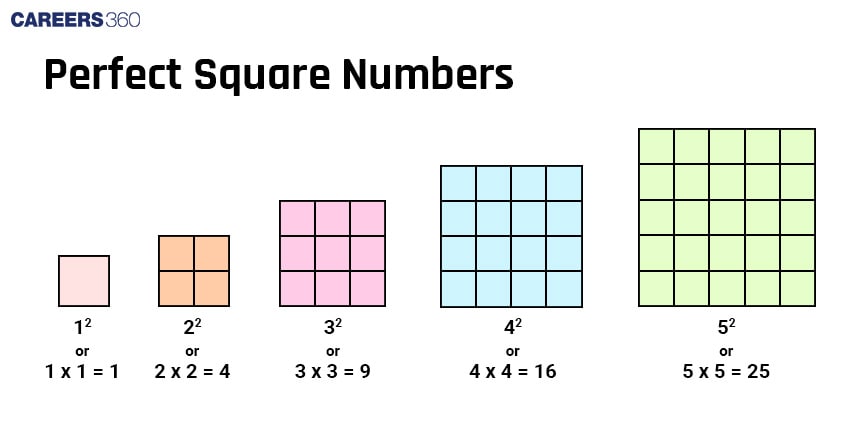
If a number can be expressed as the product of an integer with itself, then that number is called a Perfect square.
In other words, a number "a" is a perfect square if there exists an integer "b" such that a = b²

Example: 4 is a perfect square as 4 = 2², 9 is a perfect square as 9 = 3²

Properties of perfect squares

1. Non-Negative Perfect Squares:

Perfect squares are always non-negative numbers.
If we multiply two negative numbers, we will get a positive number all the time (example: –8 × –8 = +64)
or if we multiply two positive numbers, the resultant number always is positive (Example: +8 × +8 = +64).

2. Square Root of a perfect square:

The square root of a perfect square is always an integer.
Example: 9=3, which is an integer, 121=11, which is an integer

3. Last digit of perfect square:

Most of the time Perfect squares end with the integers 0, 1, 4, 5, 6, or 9, but never in 2, 3, 7, or 8, when expressed in the base 10.
Example: 100(10²), 121(11²), 144(12²), 225(15²), 196(14²), 169(13²),...

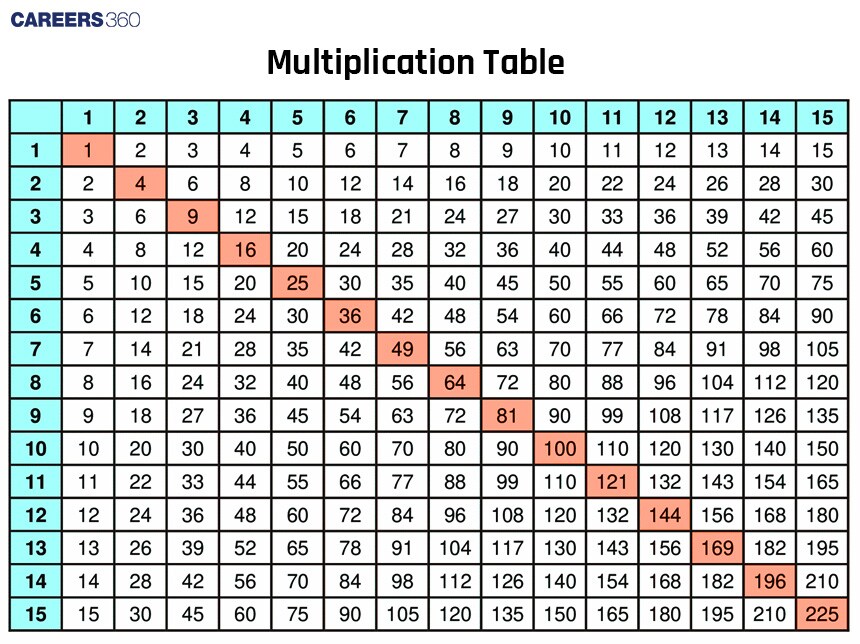
Squares table up to 50

Factors of a perfect square

To explain, the factors of a perfect square, let's take an example.

64 is a perfect square. Why?

Unlike most numbers, perfect squares have an odd number of total factors. This is because one of the factors (the square root of the perfect square) is repeated.
Factors of 64 are 1, 2, 4, 8, 14, 32, 64.

Factors can be paired as follows.
1 × 64 = 64

2 × 32 = 64

4 × 16 = 64

8 × 8 = 64

As we can see 8 is repeated, so it is a perfect square number.

Is 50 a perfect square number?

Factors of 50 are 1, 2, 5, 10, 25, 50.

Factors can be paired as follows.
1 × 50 = 50

2 × 25 = 50

5 × 10 = 50

As we can there are no factors repeated, so 50 is not a perfect square.

Prime Factorization Approach

The prime factorisation of a perfect square provides insight into its factors. All the exponents in its prime factorisation must be even in a perfect square.

100 is a perfect square number. Why?

100 = 2 × 2 × 5 × 5 = 2² × 5²

As we can see, here the exponents of 2 and 5 are even.
So, 100 is a perfect square.

Is 216 a perfect square?

216 = 2 × 2 × 2 × 3 × 3 × 3 = 2³ × 3³

As we can see, here the exponents of 2 and 3 are uneven.
So, 216 is not a perfect square.
But if we multiply it with one more 2 and 3, then exponents will be even and the resultant number will be a perfect square number.

How to find the square root of a perfect square number?

The three most common methods to find the square root of a perfect square are:

1. Prime factorisation method

2. Long division method

3. Estimation method

1. Prime Factorisation Method

In the Prime factorisation method, we express the number as a product of prime factors and then pair the factors to find the square root. It is the most commonly used method.

Step 1: Factorize the number into its prime factors.

Step 2: Pair the same type of prime factors.

Step 3: Multiply one number from each pair to get the required square root.

Example:

Find the square root of 225.

⇒ The prime factors of 225 = 3 × 3 × 5 × 5 = 3² × 5²

Taking one number from each pair, we get 3 × 5 =15

So, the square root of 225 is 15.

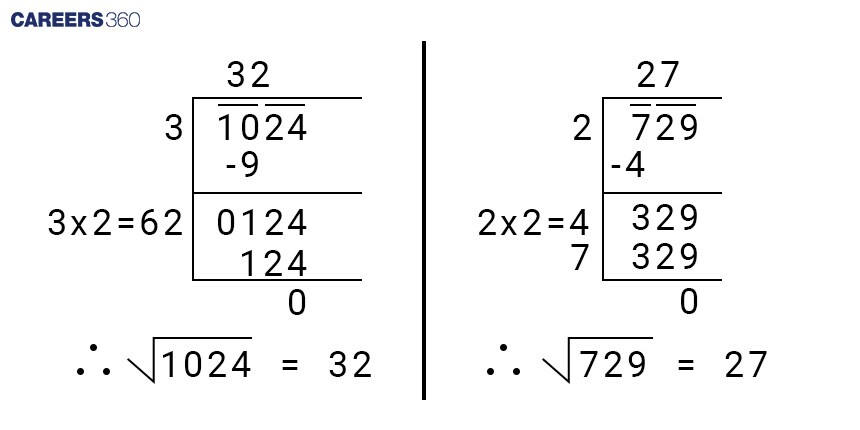
2. Long Division Method

The long division method is useful for larger numbers or when precision is necessary without a calculator.

Step 1: Group the digits of the number in pairs from right to left and place a bar above their head. If there is an odd number of digits, put a bar on the leftmost digit.

Step 2: Find the largest number whose square is less than or equal to the first group of digits.

Step 3: Subtract this square from the first group and bring down the next pair of digits.

Step 4: Double the divisor and find a digit that, when added to the divisor and multiplied by the new digit, is less than or equal to the current dividend.

Step 5: Repeat this process until all pairs have been processed and the remainder is 0 or less than the divisor.

3. Estimation method

The estimation method is useful for larger numbers or when a rough estimate is sufficient.

Step 1: Take one immediate next perfect square and the nearest preceding perfect square of the number.

Step 2: Then check the number is closer to which number.

Step 3: Take an educated guess then what the number will be.

Example:

Find the square root of 200.

⇒ 196 < 200 < 225

So, 142 < 200 < 152

So, the square root of 200 lies between 14 and 15, but closer to 14.
∴200≈14

An educated guess will be 14.1 as the number is very close to the square of 14, which is correct.

Perfect Cubes

If a number can be expressed as the product of an integer multiplied by itself three times, then that number is called a Perfect cube.

In other words, a number "a" is a perfect cube if there exists an integer "b" such that a = b3

Example: 8 is a perfect cube as 8 = 2³, 27 is a perfect cube as 27 = 3³

Properties of perfect cubes

1. Positive and Negative Perfect Cubes:

Perfect cubes can be positive or negative integers unlike perfect squares, which were always non-negative integers.
Example: −27 is a perfect cube as −27 = (−3)³, −125 is a perfect square as −125 = (−5)³

2. Cube root of a perfect cube:

The cube root of a perfect cube is always an integer.
Example: 93=3, which is an integer, 643=4, which is an integer

3. Last digit of a perfect cube:

In base 10, a perfect cube can end in any digit, unlike perfect squares which have more restricted ending digits.

Example: 343(7³), 512(8³), 1728(12³), 2197(13³)
In these examples, the Perfect cube ending digits have 3, 2, 8, 7. These digits do not generally come up at the end of a Perfect square.

Cubes table up to 50

Factors of a perfect cube

Let's take an example to understand the factors of a cube better.

27 is a perfect cube. Why?

Factors of a perfect cube will always be paired as the multiple of the cube number.

27 is the cube of 3.
Factors of 27 are 1, 3, 9, 27.

Factors can be paired as follows.
1 × 27(3 × 3 × 3) = 27

3 × 9(3 × 3) = 27

As we can all the pairs are multiple of 3.
So, 27 is a perfect cube number.

Is 30 a perfect cube?

Factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30.

Factors can be paired as follows.
1 × 30(2 × 3 × 5) = 30

2 × 15(3 × 5) = 30

3 × 10(2 × 5) = 30

5 × 6(2 × 3) = 30

Here pairs don't have multiple of any specific number like the above example.
So, 30 is not a perfect cube.

Prime Factorization Approach

The prime factorisation of a perfect cube provides insight into its factors. All the exponents in its prime factorisation must be multiple of 3.

125 is a perfect cube number. Why?

125 = 5 × 5 × 5 = 5³

As we can see, here the exponent of 5 is a multiple of 3.

So, 125 is a perfect cube.

Is 100 a perfect cube?

100 = 2 × 2 × 5 × 5 = 2² × 5²

As we can see, here the exponents of 2 and 5 are not a multiple of 3.

So, 100 is not a perfect cube.

But if we multiply it with one more 2 and 5, then exponents will be multiple of 3 and the resultant number will be a perfect cube number.

How to find the root of a perfect cube number?

The three most common methods to find the cube root of a perfect cube are:

1. Prime factorisation method

2. Estimation method

3. Direct calculation method for small numbers

1. Prime Factorisation Method

In the Prime factorisation method, we express the number as a product of prime factors and then group the factors into triplets to find the cube root. It is the most commonly used method.

Step 1: Factorize the number into its prime factors.

Step 2: Group the triplets of the same type of prime factors.

Step 3: Multiply one number from each triplet to get the required square root.

Example:

Find the cube root of 512.

The prime factors of 512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2³ × 2³ × 2³

Taking one number from each pair, we get 2 × 2 × 2 = 8

So, the cube root of 512 is 8.

2. Estimation Method

The estimation method is useful for larger numbers or when a rough estimate is sufficient.

Step 1: Take one immediate next perfect cube and the nearest preceding perfect cube of the number.

Step 2: Then check the number is closer to which number.

Step 3: Take an educated guess then what the number will be.

Example:

Find the cube root of 250.

⇒ 216 < 250 < 343

So, 63 < 200 < 73

So, the cube root of 250 lies between 6 and 7, but closer to 6.
∴2503≈6

An educated guess will be 6.3, which is correct.

3. Direct Calculation Method For Small Numbers

For small perfect cubes, we can directly calculate the cube root by identifying the integer whose cube is the given number.

Example:

Find the cube root of 8.

8 = 2³

So, the cube root of 8 is 2.

Can a number be both a perfect square and a perfect cube?

A number can be both a perfect square and a perfect cube. Those numbers are known as perfect sixth powers. This is because a number that is both a perfect square and a perfect cube must be raised to the power of 6.

We will take an example to understand it better.

64 is a perfect square.

64 = 8²

Also, 64 is a perfect cube.

64 = 4³

So, we can write 64 in terms of the sixth power as 2⁶.

The same can be said for 1 and 729.

Practice Questions

Q1. The least number that divides 37044, gives the result in a perfect cube, is:

1. 2

2. 4

3. 14

4. 21

Hint: Factorise 37044 and find which numbers are not in a set of 3.

Answer:

We have to find the smallest number that divides 37044 and results in a perfect cube.

Here, 37044 = 2 × 2 × 3 × 3 × 3 × 7 × 7 × 7

= 4 × 3³ × 7³

= 4 × (21)³

Therefore, the smallest number that divides 37044 and results in a perfect cube is 4.

Hence, the correct answer is 4.

Q2. Find the value of: 138243

1. 38

2. 36

3. 24

4. 28

Hint: Factorise 13824 and find whose cube equals to 13824.

Answer:

Here, 13824 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3

= 2³ × 2³ × 2³ × 3³

= (2 × 2 × 2 × 3)³

= (24)³

∴138243 = 24

Hence, the correct answer is 24.

Q3. What is the smallest two-digit perfect cube?

1. 25

2. 27

3. 16

4. 64

Hint: Find the perfect cube root of the given options.

Answer:

⇒ 251/3 = 52/3

This is not a perfect cube.

⇒ 271/3 = 33/3 = 3

This is a perfect cube.

⇒ 161/3 = 24/3 = 2 × (21/3)

This is not a perfect cube.

⇒ 641/3 = 43/3 = 4

This is a perfect cube.

Thus, 27 and 64 are perfect cubes of numbers and 27 is the smallest.

Hence, the correct answer is 27.

Q4. What is the smallest number by which 625 must be divided so that the quotient is a perfect cube?

1. 25

2. 5

3. 3

4. 2

Hint: A perfect cube has multiples of 3 as powers of prime factors.

Answer:

We know, a perfect cube has multiples of 3 as powers of prime factors.

So, 625 = 5⁴

Hence, 625 can be made a perfect cube by dividing it by 5.

After dividing 625 by 5 we get 125 = 5³

Hence, the correct answer is 5.

Q5. A teacher wants to arrange his students in an equal number of rows and columns. If there are 1369 students, the number of students in the last row is:

1. 37

2. 32

3. 63

4. 47

Hint: The total number of students in a class is found by multiplying the number of rows and columns of the class.

Answer:

The teacher wants to arrange the students in a square formation, where the number of rows equals the number of columns.

The number of students, 1369, is a perfect square (since 37² = 1369).

Therefore, the teacher can arrange the students in 37 rows with 37 students in each row.

Hence, the correct answer is 37.

Q6. What is the least number that can be multiplied by 69120 to make it a perfect cube?

1. 10

2. 50

3. 25

4. 5

Hint: For the number to be a perfect cube, all the exponents must be multiples of 3.

Answer:

Prime factorization of 69120=29×33×5

For the number to be a perfect cube, all the exponents must be multiples of 3, thus the above number must be multiplied by 52=25

Hence, the correct answer is 25.

Q7. The cube of the sum of two given numbers is 1728, while the product of the two given numbers is 32. Find the positive difference between the cubes of the two given numbers.

1. 448

2. 576

3. 480

4. 512

Hint: Let the two numbers be a and b

First, find a+b and then find a−b using formula (a+b)2−(a−b)2=4ab and then solve for a and b.

Answer:

Let the two numbers be a and b

(a+b)3=1728

⇒ a+b=17283=12............I

ab=32 given,

Now,

(a+b)2−(a−b)2=4ab

⇒ (a−b)2=122−4×32

⇒ (a−b)2=16

⇒ a−b=4.................II

By adding eq. I and eq. II

2a=16

⇒ a=8

Put a=8 in eq. I

⇒ 8+b=12

⇒ b=4

So from this, we know the numbers are 8 and 4.

The positive difference between the cubes of these numbers =(83−43)=512−64=448

Hence, the correct answer is 448.

Q8. By what the least number should 4320 be multiplied to obtain a number that is a perfect cube?

1. 40

2. 50

3. 60

4. 80

Hint: Factorise the given number to get the required value.

Answer:

4320 = 3 × 3 × 3 × 2 × 2 × 2 × 2 × 2 × 5 = 3³ × 2⁵ × 5

We need one 2's and two 5's to make a cube.

Thus, the numbers should be multiplied as 2 × 5² = 2 × 2⁵ = 50

Hence, the correct answer is 50.

Q9. For what value of N, the number 34N will be a perfect cube, where 34N is a 3-digit number?

1. 2

2. 3

3. 4

4. 5

Hint: Check for the perfect cube between 340 and 349.

Answer:

We know the nearest cube to 34N is 73 = 343

So, for N = 3, 34N will be a perfect cube.

Hence, the correct answer is 3.

Q10. What is the smallest value that must be added to 709, so that the resultant is a perfect square?

1. 8

2. 12

3. 20

4. 32

Hint: First, find a perfect square number near the given number. Then take the difference to solve it.

Answer:

709 + x = perfect square

The perfect square nearest to 709 is 729 = 272

∴x = 729 – 709 = 20

Hence, the correct answer is 20.

Q11. The smallest whole number that is to be multiplied by 59535 to make a perfect square is x. The sum of digits of x is:

1. 9

2. 5

3. 7

4. 6

Hint: First, factorize the given number. Then, find out the number that needs to be multiplied to make it a perfect square.

Answer:

Factorization of the 59535 = 5 × 3⁵ × 7²

It needs to be multiplied by 5 × 3 = 15 to get a perfect square.

∴ Sum of digits = 1 + 5 = 6

Hence, the correct answer is 6.

Q12. The least number that should be subtracted from the number 32146 to make it a perfect square is:

1. 305

2. 105

3. 605

4. 205

Hint: Try to find the nearest perfect square number of 32146.

Answer:

We know the value of (180)² = 32400

Then, the least number subtracted from 32146 to make it perfect square = 32146 – (179)²

= 32146 – 32041 = 105

Hence, the correct answer is 105.

Q13. Some boys raised Rs. 12,544 for a famine fund, with each boy contributing as many rupees as there were boys. The number of boys who contributed is:

1. 102

2. 112

3. 122

4. 132

Hint: Assume the total number of boys is x and each boy gives Rs. x for a famine fund. Solve by using the given conditions to find the desired value.

Answer:

Given: A number of boys raised Rs. 12544 for a famine fund.

Amount raised by each boy = the total number of boys

Let the number of boys be x.

So, the amount raised by each boy = Rs. x

As per given condition,

x2=12544

⇒x=12544

∴x=112

Hence, the correct answer is 112.

Q14. For what value of N, 270N will be a perfect square, where 270N is a 4-digit number?

1. 1

2. 6

3. 4

4. 9

Hint: First, find a perfect square number nearest the given number. Then compare it with the given number to solve this.

Answer:

270N is a 4-digit number.

A perfect square between 2700–2709 is 522 = 2704

∴ N = 4

Hence, the correct answer is 4.

Q15. What smallest value must be added to 508, so that the resultant is a perfect cube?

1. 4

2. 6

3. 8

4. 10

Hint: First, find a perfect cube number near the given number.

Answer:

508 + x = perfect cube

The perfect cube nearest to 508 is 512 = 83

∴x = 512 – 508 = 4

Hence, the correct answer is 4.