Square Root and Cube Root of Surds: Definition, Calculator, Questions, Formula

Surds are irrational numbers. Surds can not be simplified to give any rational number. We will use several specific formulas and tricks to learn how to find the square root cube root or nth root of surds. Also, there are several methods to simplify these expressions. One can find resources in the PDF form. Documents like ‘square root of surds’ provide essential concepts, formulas, and questions on finding the square root of surds.
In this article, we are going to discuss key formulas, such as the formula for the square root of surds and cube root of surds, various square root of surds problems and cube root of quadratic surd problems etc. It is very important to understand the square root of surd form and one should focus on the positive square root of surds as well as the negative square root of the surds. This article also involves the methods for how to calculate cube roots of surds.

Square roots and Cube roots: An Overview

Square roots and cube roots are fundamental operations in mathematics. The square root of a number $x$ is a value $y$ such that $y^2 = x$, and the cube root of $x$ is a value $y$ such that $y^3 = x$. These operations are crucial for solving equations, simplifying expressions, and understanding various mathematical concepts.

How to find the Square root of a number

Finding the square root of a number is a fundamental mathematical operation that involves determining a number that, when multiplied by itself, yields the original number. Various methods such as long division, factorisation, and approximation are used to compute square roots accurately.

Long Division Method

The long division method for finding the square root of a number involves a step-by-step process of division and estimation. Here’s how it works:

• Step 1: Group the number into pairs of digits starting from right to left.

• Step 2: Starting with the leftmost pair, find the largest integer whose square is less than or equal to the first pair of digits. This forms the first part of the square root.

• Step 3: Subtract the square of this integer from the original pair and bring down the next pair of digits to form a new dividend.

• Step 4: Double the current part of the square root found so far and find the next digit that, when multiplied by itself, gives a number close to the new dividend.

• Step 5: Repeat steps 3 and 4 until all pairs of digits have been used, forming the complete square root.

Example: Find the square root of 1225 using the long division method.

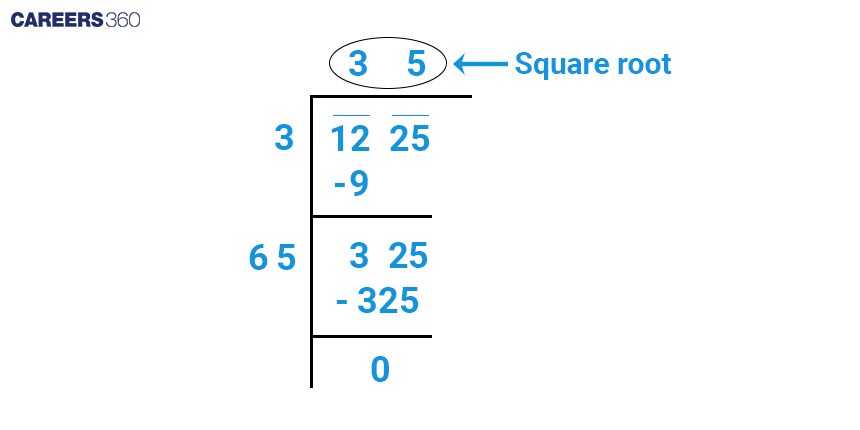
Method of factor

The factorisation method for finding the square root of a number involves the following steps:

• Step 1: Factorize the number into its prime factors.

• Step 2: Take one factor from each pair of these prime factors.

• Step 3: Multiply these to obtain the square root.

Example: Find the square root of 324 using the factorisation method.

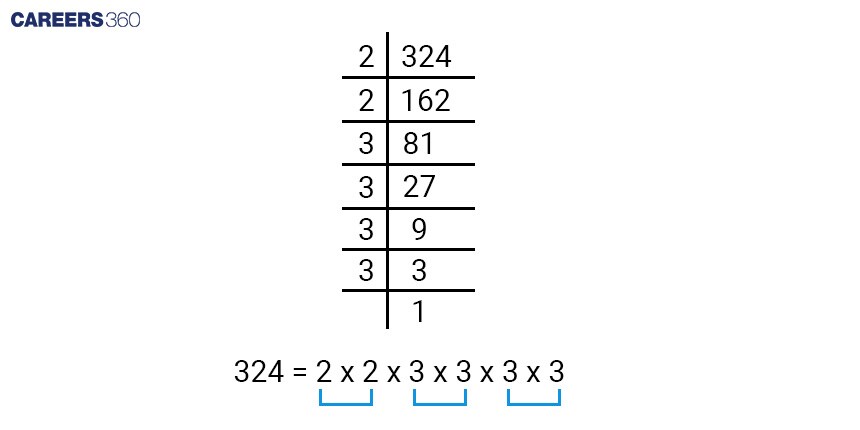
So, the square root of 324 is (2 × 3 × 3) = 18.

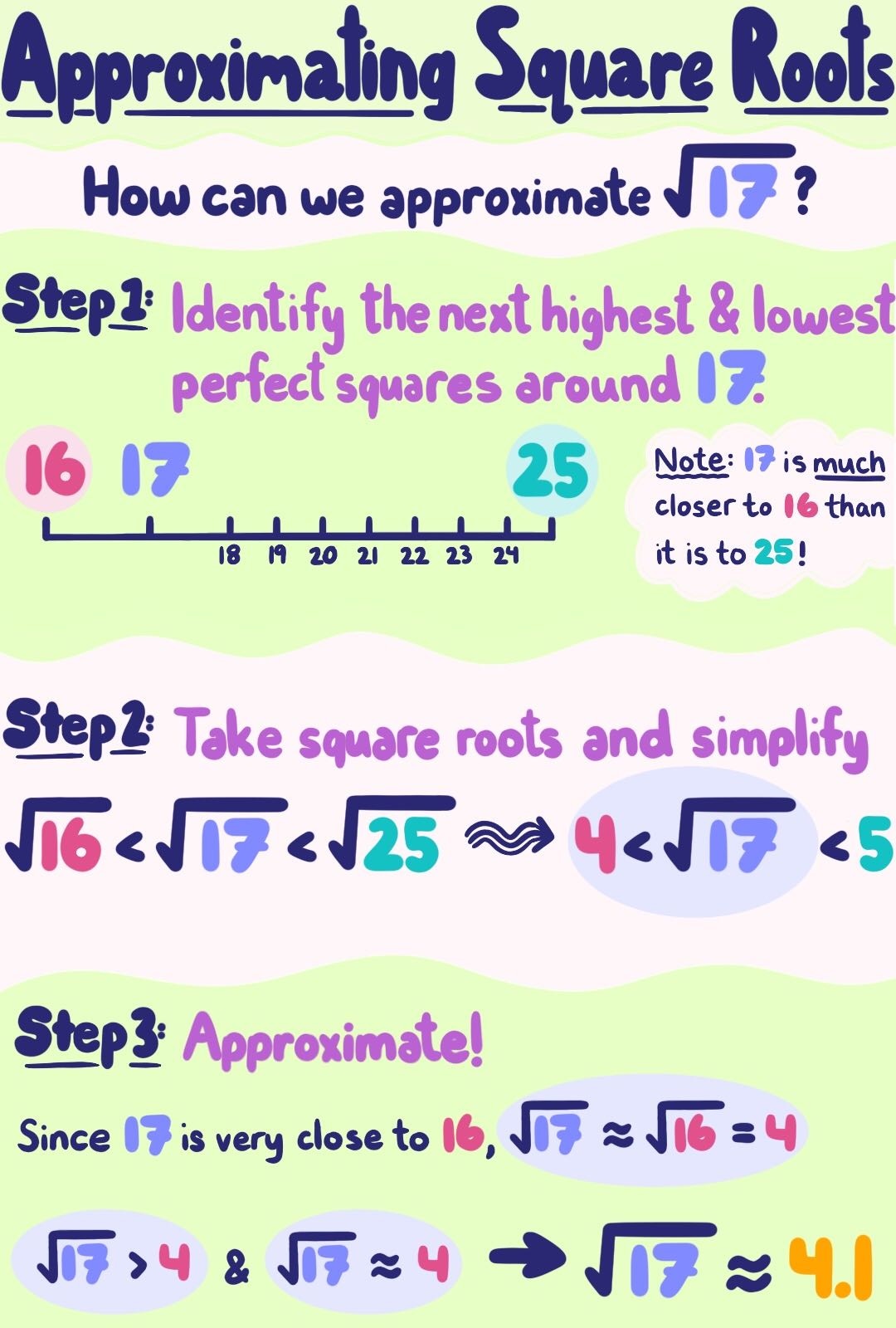
Method of Approximation

This method involves estimating the square root by identifying two close perfect squares and interpolating them.

The square root of a Surd

The square root of a surd refers to simplifying an expression that contains a square root of a number that is not a perfect square. Surds often involve radicals (square roots) of numbers that cannot be simplified further into rational numbers. Finding the square root of a surd typically involves using algebraic techniques to express it in a simplified form.

Steps to find the square root of a surd

Let’s find the square root of the surd ($a+\sqrt{b}$) following these general steps:

• Use the formula, $(a + b)^2 = a^2 + 2ab + b^2$, to simplify the expression of $\sqrt{a + \sqrt{b}}$.

• Identify $x$ and $y$ such that $\sqrt{a + \sqrt{b}} = (\sqrt{x} + \sqrt{y})^2$.

• The square root of ($a+\sqrt{b}$) will be $(\sqrt{x} + \sqrt{y})$.

Example: Find the square root of $(9+4\sqrt{5})$.

Here, $9+4\sqrt{5}$ = $4+5+4\sqrt{5}$ = $(2)^2+2×2×\sqrt{5}+(\sqrt{5})^2$ = $(2+\sqrt{5})^2$

Hence, the square root of $(9+4\sqrt{5})$ is $(2+\sqrt{5})$ or $-(2+\sqrt{5})$.

How to find the Cube root of a number

Finding the cube root of a number involves determining a value which, when multiplied by itself three times, equals the original number. There are various ways to find the cube root of a number, let's discuss them with proper examples.

Method of factor

This method is similar to finding the square root by factorisation but involves triplets of factors. Finding the cube root of a number using the factorization method involves the following steps:

• Break down the number into its prime factors.

• Group the prime factors into sets of three identical factors.

• For each group of three identical factors, take one factor out of the group.

• Multiply these factors together to get the cube root of the original number.

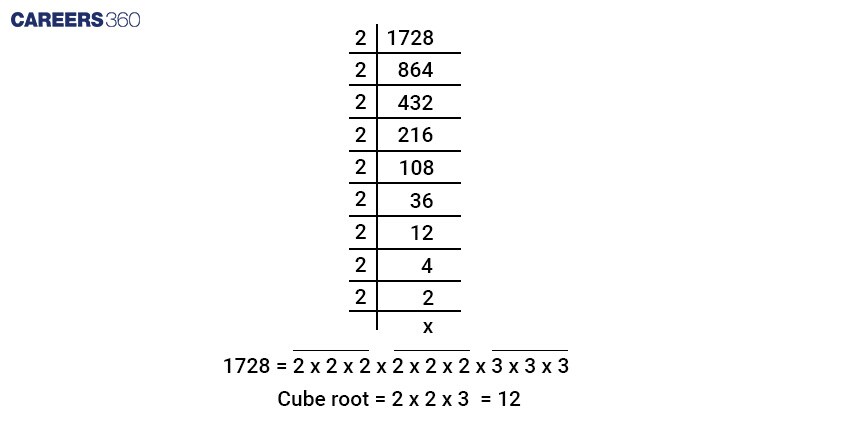
Example: Find the cube root of 1728 using the factorisation method.

Method of Approximation

Estimate the cube root by identifying two close perfect cubes.

Example: Find the cube root of 17 using the approximation method.

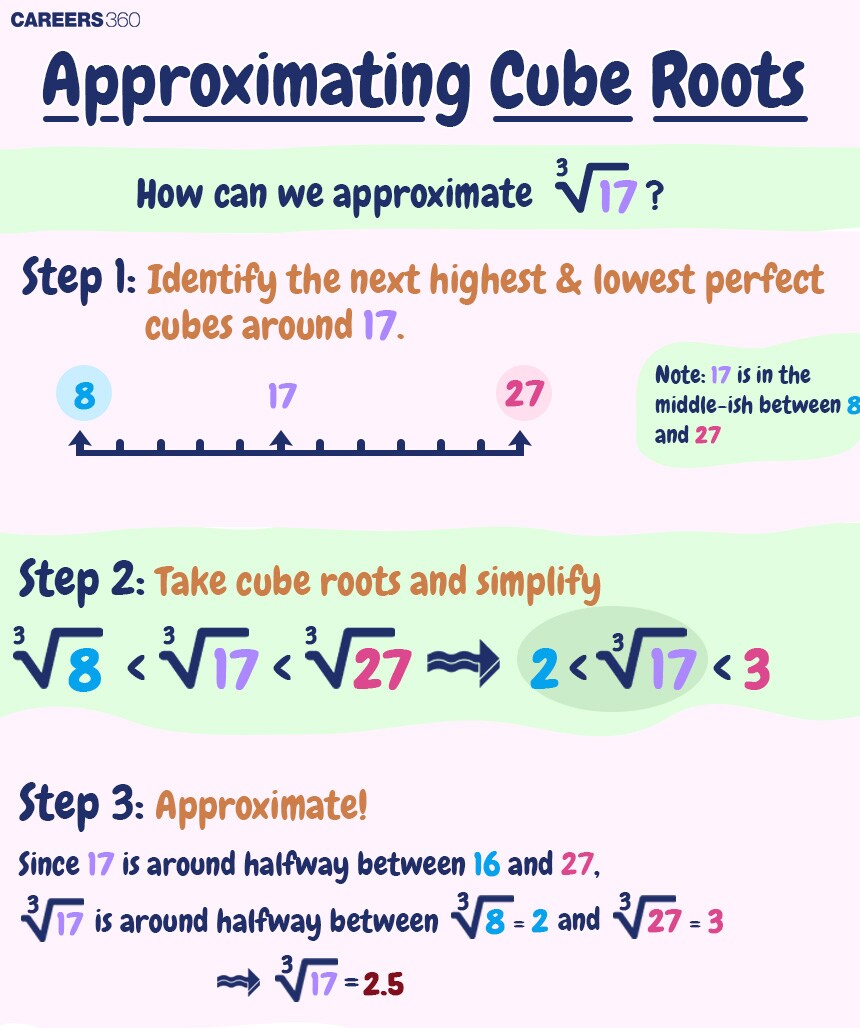
Cube root of a Surd

The cube root of a surd involves simplifying an expression that includes a cube root of a number that is not a perfect cube. Finding the cube root of a surd generally requires using algebraic methods such as using specific formulas to simplify and express the cube root in its simplest form.

Steps to find the cube root of a surd

Let’s find the cube root of the surd ($a+\sqrt{b}$) following these general steps:

• Use the formula, $(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$, to simplify expression of $\sqrt{a + \sqrt{b}}$.

• Identify $x$ and $y$ such that $\sqrt{a + \sqrt{b}} = (\sqrt{x} + \sqrt{y})^3$.

• The cube root of ($a+\sqrt{b}$) will be $(\sqrt{x} + \sqrt{y})$.

Example: Find the cube root of $10 + 6\sqrt{3}$.

Here, $10 + 6\sqrt{3}$

= $1 + 9 + 3\sqrt{3} + 3\sqrt{3}$

= $(1)^3 + 3×(1)^2×(\sqrt{3}) + 3×(1)×(\sqrt{3})^2 + (\sqrt{3})^3$

= $(1+\sqrt{3})^3$

So, the cube root of $10 + 6\sqrt{3}$ is $(1+\sqrt{3})$.

Tips and Tricks

• Memorize common squares and cubes to quickly identify roots.

• Practice using different methods to become proficient in finding roots.

• For surds, always simplify inside the radical as much as possible before finding the root.

• Use approximation methods to estimate roots when exact calculation is difficult.

Practice Questions/Solved Examples

Q.1.

If $9\sqrt{x}=\sqrt{12}+\sqrt{147}$, then $x$ =?

1. 5

2. 3

3. 2

4. 4

Hint: Simplify the square roots and solve.

Solution:

$9\sqrt{x} = \sqrt{12} + \sqrt{147}$

⇒ $9\sqrt{x} = 2\sqrt{3} + 7\sqrt{3}$

⇒ $9\sqrt{x} = 9\sqrt{3}$

$\therefore x = 3$

Hence, the correct answer is option (2).

Q.2.

$2\sqrt{54}-6\sqrt{\frac{2}{3}}-\sqrt{96}$ is equal to:

1. $\sqrt{6}$

2. $0$

3. $1$

4. $2$

Hint: Simplify the square roots and solve to get the required answer.

Solution:

Given:

$2\sqrt{54}-6\sqrt{\frac{2}{3}}-\sqrt{96}$

= $6\sqrt{6}-6\sqrt{\frac{2}{3}}-4\sqrt{6}$

= $2\sqrt{6}-6\sqrt{\frac{2}{3}}$

= $2\sqrt{2}\sqrt{3}-6\frac{\sqrt{2}}{\sqrt{3}}$

= $\frac{2\sqrt{2}×3-6\sqrt{2}}{\sqrt{3}}$

= $\frac{6\sqrt{2}-6\sqrt{2}}{\sqrt{3}}$

= $0$

Hence, the correct answer is option (2).

Q.3.

$\frac{\sqrt{24}+\sqrt{216}}{\sqrt{96}}$ is equal to:

1. 1

2. 6

3. 8

4. 2

Hint: Simplify the square roots and solve to get the required answer.

Solution:

Given:

$\frac{\sqrt{24}+\sqrt{216}}{\sqrt{96}}$

= $\frac{2\sqrt{6}+6\sqrt{6}}{4\sqrt{6}}$

= $\frac{8\sqrt{6}}{4\sqrt{6}}$

= $2$

Hence, the correct answer is option (4).

Q.4.

What is the value of $\sqrt{1509+\sqrt{144}}?$

1. 39

2. 37

3. 41

4. 49

Hint: Use the values of square roots of 144 and 1521.

Solution:

$\sqrt{1509+\sqrt{144}} = \sqrt{1509+12}=\sqrt{1521}=39$

Hence, the correct answer is option (1).

Q.5.

What is the simplified value of $\frac{33}{(6–\sqrt3)}$?

1. $6+\sqrt3$

2. $6-\sqrt3$

3. $12+\sqrt3$

4. $12-\sqrt3$

Hint: Multiply $(6+\sqrt3)$ with the numerator and denominator.

Solution:

$\frac{33}{(6–\sqrt3)}$

$=\frac{33}{(6–\sqrt3)}×\frac{(6+\sqrt3)}{(6+\sqrt3)}$

$=\frac{33(6+\sqrt3)}{33}$

$=(6+\sqrt3)$

Hence, the correct answer is option (1).

Q.6.

If $a = 64$ and $b = 289$, then the value of $\sqrt{\sqrt{\sqrt{a}+\sqrt{b}}-\sqrt{\sqrt{b}-\sqrt{a}}}$ is:

1. $2^{\frac{1}{2}}$

2. $2$

3. $4$

4. $–1$

Hint: Determine the solution by substituting the values in the expression and solve.

Solution:

Given: $a = 64$ and $b = 289$

The given expression is $\sqrt{\sqrt{\sqrt{a}+\sqrt{b}}-\sqrt{\sqrt{b}-\sqrt{a}}}$.

Substitute the value of $a = 64$ and $b = 289$ in the above equation, we get,

$=\sqrt{\sqrt{\sqrt{64}+\sqrt{289}}-\sqrt{\sqrt{289} - \sqrt{64}}}$

$=\sqrt{\sqrt{8+17}-\sqrt{17-8}}$

$=\sqrt{\sqrt{25}-\sqrt{9}}$

$=\sqrt{5-3}$

$=2^{\frac{1}{2}}$

Hence, the correct answer is option (1).

Q.7.

The square root of $\frac{2+\sqrt{3}}{2}$ is:

1. $\pm \frac{1}{\sqrt{2}}(\sqrt{3}+1)$

2. $\pm \frac{1}{2}(\sqrt{3}-2)$

3. $\text{none}$

4. $\pm \frac{1}{2}(\sqrt{3}+1)$

Hint: Write $\frac{2+\sqrt{3}}{2}$ in the form of $\frac{1}{4}({4+2\sqrt{3}})$ to make it perfect square.

Solution:

Given: $\frac{2+\sqrt{3}}{2}$

$= \frac{1}{4}({4+2\sqrt{3}})$

$= \frac{1}{4}[1^2+(\sqrt{3})^2+2×1×\sqrt{3}]$

$= \frac{1}{4}(1+\sqrt{3})^2$

So, the square root of $\frac{2+\sqrt{3}}{2}$

$= \sqrt{\frac{2+\sqrt{3}}{2}}$

$= \sqrt{\frac{1}{4}(1+\sqrt{3})^2}$

$= \pm \frac{1}{2}(1+\sqrt{3})$

Hence, the correct answer is option (4).

Q.8.

If $(2+\sqrt{3})a=(2-\sqrt{3})b=1$, then the value of $\frac{1}{a}+\frac{1}{b}$ is:

1. $1$

2. $2$

3. $2\sqrt{3}$

4. $4$

Hint: Find the value of $\frac{1}{a}$ and $\frac{1}{b}$ by cross multiplication. Use this information to solve the question.

Solution:

$(2+\sqrt{3})a=(2-\sqrt{3})b=1$

$(2+\sqrt{3})a=1$

$⇒ a = \frac{1}{2+\sqrt{3}}$

$⇒ \frac{1}{a} = 2-\sqrt{3}$

Again, $(2-\sqrt{3})b=1$

$⇒ b = \frac{1}{2-\sqrt{3}}$

$⇒ \frac{1}{b} = 2+\sqrt{3}$

$\frac{1}{a} + \frac{1}{b}=2-\sqrt{3}+2+\sqrt{3}$

$\frac{1}{a} + \frac{1}{b}=4$

Hence, the correct answer is option (4).

Q.9.

If $2x=\sqrt{a}+\frac{1}{\sqrt{a}}, a>0$, then the value of $\frac{\sqrt{x^{2}-1}}{x-\sqrt{x^{2}-1}}$ is:

1. $a+1$

2. $\frac{1}{2}(a+1)$

3. $\frac{1}{2}(a–1)$

4. $a–1$

Hint: Find the value of $x$ and ${\sqrt{x^{2}-1}}$ separately and place it in the equation to get the answer.

Solution:

Given: $2x=\sqrt{a}+\frac{1}{\sqrt{a}}, a>0$

$⇒2x=\sqrt{a}+\frac{1}{\sqrt{a}}$

$⇒x=\frac{1}{2}(\sqrt{a}+\frac{1}{\sqrt{a}})$

Calculating the value of ${\sqrt{x^{2}-1}}$

$⇒{\sqrt{x^{2}-1}}={\sqrt{(\frac{1}{2}(\sqrt{a}+\frac{1}{\sqrt{a}}))^{2}-1}}$

$⇒{\sqrt{(\frac{a^2-2a+1}{4a})}}=\frac{a-1}{2\sqrt{a}}$

So that $\frac{\sqrt{x^{2}-1}}{x-\sqrt{x^{2}-1}}$ becomes

$⇒\frac{\sqrt{x^{2}-1}}{x-\sqrt{x^{2}-1}}=\frac{\frac{a-1}{2\sqrt{a}}}{\frac{1}{2}(\sqrt{a}+\frac{1}{\sqrt{a}})-(\frac{a-1}{2\sqrt{a}})}$

$⇒\frac{\sqrt{x^{2}-1}}{x-\sqrt{x^{2}-1}}=\frac{a-1}{2\sqrt{a}}×\frac{2\sqrt{a}}{2}=\frac{1}{2}(a–1)$

Hence, the correct answer is option (3).

Q.10.

Which of the following statement(s) is/are true?

I. $\sqrt{144}\times \sqrt{36}<\sqrt[3]{125}\times \sqrt{121}$

II. $\sqrt{324}+ \sqrt{49}<\sqrt[3]{216}\times \sqrt{9}$

1. Only I

2. Only II

3. Neither I nor II

4. Both I and II

Hint: Use mathematical operations like square roots, cube roots, addition, and multiplication.

Solution:

I. $\sqrt{144}\times \sqrt{36}<\sqrt[3]{125}\times \sqrt{121}$

On the left side, $\sqrt{144} = 12$ and $\sqrt{36} = 6$, so their product is $12 \times 6 = 72$.

On the right side, $\sqrt[3]{125} = 5$ and $\sqrt{121} = 11$, so their product is $5 \times 11 = 55$.

So, the inequality $72 < 55$ is not true.

II. $\sqrt{324}+ \sqrt{49}<\sqrt[3]{216}\times \sqrt{9}$

On the left side, $\sqrt{324} = 18$ and $\sqrt{49} = 7$, so their sum is $18 + 7 = 25$.

On the right side, $\sqrt[3]{216} = 6$ and $\sqrt{9} = 3$, so their product is $6 \times 3 = 18$.

So, the inequality $25 < 18$ is not true.

Therefore, the answer is neither I nor II.

Hence, the correct answer is option (3).