Surface Area and Volume of a Prism: Formula, Calculator

The surface area and volume of a Prism is an important chapter of 3d geometry. Prisms can be of many different types such as triangular, rectangular, or pentagonal etc. We will discuss 'Surface Area and Volume of a Prism', 'Surface area and volume of a prism formula', 'Surface area and volume of a prism worksheet', 'Surface area and volume of a prism calculator', 'Surface area and volume of a rectangular prism', 'Surface area and volume of a triangular prism', 'Surface area and volume of a triangular prism calculator', 'Surface area and volume of a rectangular prism formula', and 'Surface area and volume of a hexagonal prism' etc.

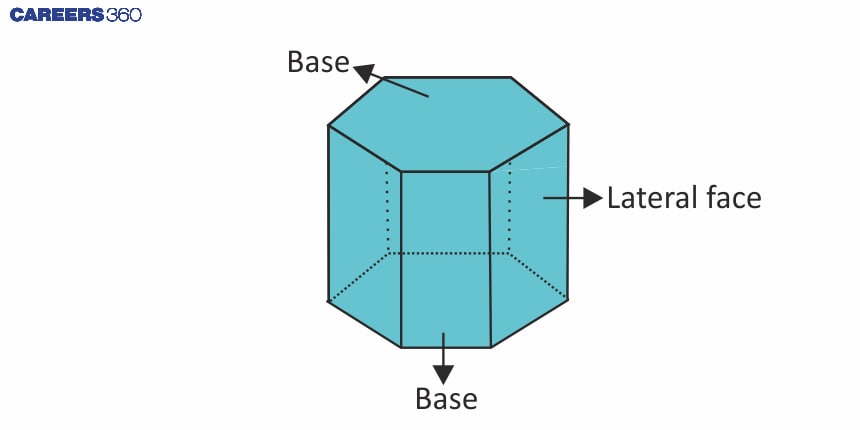
Prism: An Overview

A prism is a three-dimensional object with two parallel, congruent bases covered by rectangular or parallelogram faces. The bases can be of any shape. According to the shapes of their bases, prisms are called triangular, rectangular, and hexagonal.

Examples of Prism

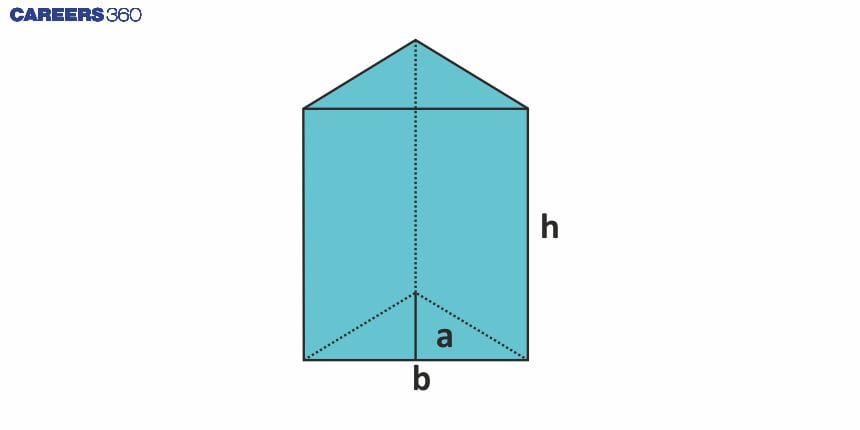
• Triangular Prism: A tent with triangular faces.

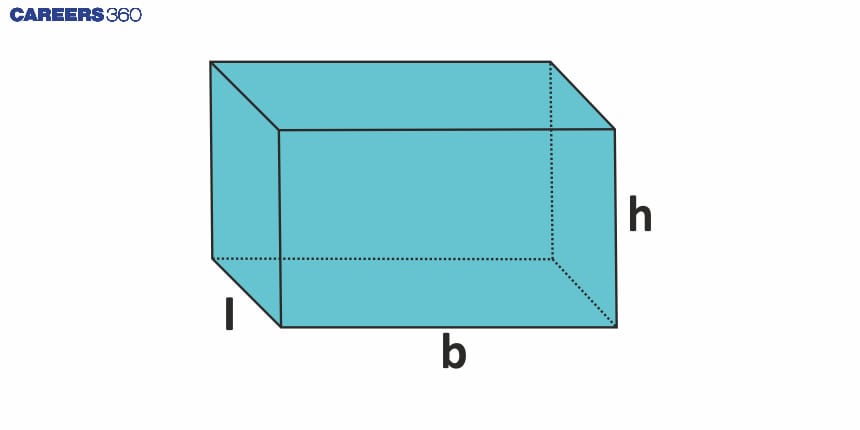
• Rectangular Prism: A common brick or a shoebox.

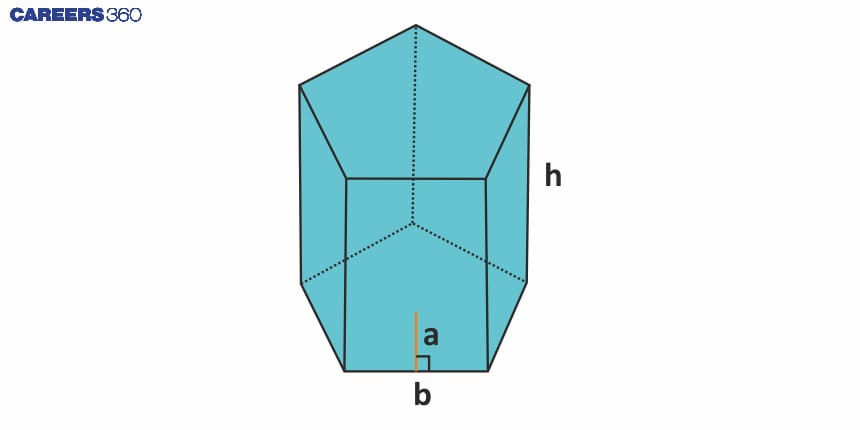
• Pentagonal Prism: A cross-section of certain complex buildings.

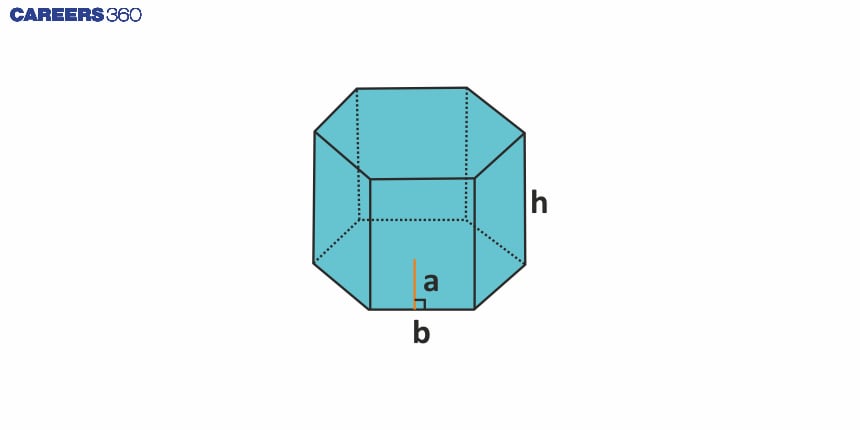
• Hexagonal Prism: Some nuts and bolts.

What is the Surface area of a Prism?

The surface area of a prism is the total area of all of its faces, including the base, top, and lateral surfaces. It helps in determining how much material is needed to cover the prism.

The formula for the surface area of a Prism

There are two types of formulas for the surface area of a prism, one is the lateral surface area and the other is the total surface area of a prism.

Lateral Surface Area of a Prism

The lateral surface area (LSA) is the sum of the areas of all the lateral faces (the faces excluding the bases).

So, LSA = Perimeter of the Base × Height

The Total surface area of a Prism

The total surface area (TSA) includes the lateral surface area and the area of the two bases.

So, TSA = LSA + (2 × Area of Base)

What is the Volume of a Prism?

The volume of a prism measures the space it occupies. It is found by multiplying the area of the base by the height (the perpendicular distance between the bases).

The formula for the Volume of a Prism

Volume of a Prism = Area of the Base × Height

List of Formulas

Important points

• The base shape determines the type of prism.

• The height is the perpendicular distance between the bases.

• The lateral surface area accounts for the sides excluding the bases.

• The total surface area includes all faces of the prism.

• Volume is the product of the base area and the height.

Practice Questions/Solved Examples

Q.1.

A prism has a regular hexagonal base with a side of 6 cm. If the total surface area of the prism is 216$\sqrt3$ cm2, then what is the height (in cm) of the prism?

1. $3\sqrt3$

2. $6\sqrt3$

3. $3$

4. $6$

Hint: By using the formula: Total curved surface area of prism = 2 × (Area of base) + 6 × (Side of the base) × height

Solution:

Given: Side, $a$ = 6 cm

Let the height be $h$.

Area of the base of the hexagonal prism $=6 \times \frac{\sqrt3}{4}a^2=6 \times \frac{\sqrt3}{4} \times 6^2 = 54\sqrt3$

Total curved surface area of prism = 2 × (Area of base) + 6 × (Side of the base) × height

⇒ $216\sqrt3 = 2 \times 54\sqrt3 + 6 \times 6 \times h$

⇒ $108\sqrt3 = 36h$

$\therefore h = 3\sqrt3\ \text{cm}$

Hence, the correct answer is $3\sqrt3$.

Q.2.

The base of a prism is a right-angled triangle with two sides 5 cm and 12 cm. The height of the prism is 10 cm. The total surface area of the prism is:

1. 360 sq cm

2. 300 sq cm

3. 300 sq cm

4. 325 sq cm

Hint: Total surface area of a prism = curved surface area + 2 (area of base)

Solution:

Given: Height = 10 cm

Two sides = 5 cm and 12 cm

$\therefore$ Area of the base of the right prism = $\frac{1}{2}×5×12$ = 30 sq cm

Other side of the right-angled triangle $=\sqrt{5^2+12^2}=\sqrt{25+144} = 13$

Curved surface area = perimeter of base × height = (5 + 12 + 13) × 10 = 300 sq cm

$\therefore$ Total surface area = curved surface area + 2 (area of base) = 300 + 2 × 30 = 360 sq cm

Hence, the correct answer is 360 sq cm.

Q.3.

A right prism stands on a base 6 cm equilateral triangle and its volume is $81\sqrt3$ cm3. The height (in cm) of the prism is:

1. 9

2. 10

3. 12

4. 15

Hint: Use the formulas:

Area of equilateral triangle of side $a$ = $\frac{\sqrt{3}a^2}{4}$

Volume of a right prism = Area of base × Height

Solution:

The base of a right prism = 6 cm

Volume $= 81\sqrt3$ cm3

Area of base of prism $= \frac{\sqrt{3}}{4}×6×6 = 9\sqrt{3}$ cm2

Volume of a right prism = area of base × height

⇒ $81\sqrt3=9\sqrt{3}$ × height

⇒ Height = 9 cm

Hence, the correct answer is 9.

Q.4.

If the altitude of a right prism is 10 cm and its base is an equilateral triangle of side 12 cm, then its total surface area (in cm2) is:

1. $(5+3\sqrt3)$

2. $36\sqrt3$

3. $360$

4. $72(5+\sqrt3)$

Hint: Use the formulas:

Area of equilateral triangle of side $a =\frac{\sqrt3a^2}{4}$

The perimeter of an equilateral triangle of side $a = 3a$

Total surface area of prism = Perimeter of base × Height + 2 × Base area

Solution:

Use the formulas:

Area of equilateral triangle of side $a =\frac{\sqrt3a^2}{4}$

The perimeter of an equilateral triangle of side $a = 3a$

Total surface area of prism = Perimeter of base × Height + 2 × Base area

Height of a right prism = 10 cm

Side of an equilateral triangle, $a$ = 12 cm

Base area $= \frac{\sqrt3a^2}{4} = \frac{\sqrt3}{4}×12×12 = 36\sqrt3$cm2

Perimeter of base $= 3a = 3 × 12 = 36$ cm

Total surface area of prism = (Perimeter of base × Height + 2 × Base area)

$=36×10 + 2×36\sqrt3$

$= 360+72\sqrt3$

$= 72(5+\sqrt3)$ cm2

Hence, the correct answer is $72(5+\sqrt3)$.

Q.5.

The base of a right prism is a right-angled triangle whose sides are 5 cm, 12 cm, and 13 cm. If the area of the total surface of the prism is 360 cm2, then its height is:

1. 10 cm

2. 10 cm

3. 10 cm

4. 10 cm

Hint: Use the formulas:

Area of an equilateral triangle = $\frac{1}{2}$ × Base × Perpendicular

The perimeter of a right triangle = Base + Hypotenuse + Perpendicular

Total surface area of prism = (Perimeter of base × Height + 2 × Base area)

Solution:

The area of the total surface of the prism = 360 cm2

The base of the right-angled triangle = 5 cm

The perpendicular of the right-angled triangle = 12 cm

Hypotenuse of the right-angled triangle = 13 cm

Perimeter of base of prism = (5 + 12 + 13) = 30 cm

Base area = $\frac{1}{2}$ × base × perpendicular

= $\frac{1}{2}$ × 5 × 12

= 30 cm2

Total surface area of prism = (Perimeter of base × Height + 2 × Base area)

⇒ 360 = 30 × height + 2 × 30

⇒ Height = $\frac{360 - 60}{30}$ = 10 cm

Hence, the correct answer is 10 cm.

Q.6.

The base of the right prism, whose height is 2 cm, is a square. If the total surface area of the prism is 10 cm2, then its volume (in cm3) is:

1. 3

2. 1

3. 2

4. 4

Hint: Use the formulas:

The total surface area of the prism = curved surface area + 2 × area of base

The volume of a prism = base area × height

Solution:

Height = 2 cm

The total surface area of the prism = 10 cm2

Let the side of the base be $a$ cm.

The total surface area of the prism = curved surface area + 2 × area of base

10 = perimeter of base × height + 2 × area of base

⇒ (4 × $a$ × 2) + (2 × $a^2$) = 10

⇒ $a^2 + 4a -5$ = 0

⇒ $(a+5)(a-1)$ = 0

Since $a$ cannot be negative,

$a$ = 1

Volume = base area × height

= $(1)^2 × 2$

= 2 cm3

Hence, the correct answer is 2 cm3.

Q.7.

Let ABCDEF be a prism whose base is a right-angled triangle, where sides adjacent to 90$^{\circ}$ are 9 cm and 12 cm. If the cost of painting the prism is INR 151.20, at the rate of 20 paise per sq cm then the height of the prism is:

1. 17 cm

2. 18 cm

3. 15 cm

4. 16 cm

Hint: Use the formula:

Total surface area = perimeter of base × height + 2 × area of base

Solution:

Total surface area of prism = $\frac{\text{Total cost of painting}}{\text{Cost per sq cm}}=\frac{151.2}{0.2}$ = 756 cm2

Hypotenuse of the triangular base = $\sqrt{9^2 + 12^2}$ = $\sqrt{81 + 144}$ = $\sqrt{225}$ = 15 cm

Perimeter of base = 9 + 12 + 15 = 36 cm

Let h be the height of the prism.

Total surface area = perimeter of base × height + 2 × area of base

756 = 36 × h + 2 × $\frac{1}{2}$ × 9 × 12

⇒ 756 = 36h + 108

⇒ h = $\frac{756-108}{36}$ = $\frac{648}{36}$ = 18 cm

Hence, the correct answer is 18 cm.

Q.8.

The base of a solid right prism is a triangle whose sides are 9 cm, 12 cm, and 15 cm. The height of the prism is 5 cm. Then, the total surface area (in cm2) of the prism is:

1. 180

2. 234

3. 288

4. 270

Hint: The total surface area of a prism = 2 × The area of the base + The perimeter of the base × The height of the prism

Solution:

Given that the base of a solid right prism is a triangle whose sides are 9 cm, 12 cm, 15 cm and the height of the prism is 5 cm.

The total surface area of a prism = 2 × The area of the base + The perimeter of the base × The height of the prism

The area of the base = $\frac{1}{2}$ × 9 × 12 = 54 cm2

The perimeter of the base = 9 + 12 + 15 = 36 cm

The total surface area of a prism = 2 × 54 cm2 + 36 cm × 5 cm = 108 cm2 + 180 cm2 = 288 cm2

Hence, the correct answer is 288 cm2.