Cube: Definition in Math, Reasoning Questions, Examples

Cube is a subtopic of Logical Reasoning that appears in various exams. This topic is commonly found in many Government exams such as SSC, Railway, Defence, and other competitive exams. The questions related to this topic can be tricky, but they are generally easy and scoring, once the concept is fully understood. One should have complete knowledge of a cube and the structure of a cube to solve the questions related to this topic. In this article we will cover structure of a cube, cube reasoning questions, cube reasoning formula, cube reasoning tricks, how to solve cube reasoning etc.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: IBSAT 2024 Mock Tests | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

Question with Solutions: Missing Number | Alphabet Test | Arithmatical Problems | Calendar

This Story also Contains

1. Cube: Structure of a Cube
2. Types of Questions Asked from Cube Reasoning
3. Recommended Books and Online Resources
4. Question Weightage of Cube in Competitive Exams
5. Practice Questions For Cutting of a Cube and Counting of Smaller Cubes
6. Practice Questions For Counting of Coloured Cubes

Cube: Structure of a Cube

A cube is a 3D figure with three sides, length, breadth and height where all the sides are equal. A cube has 6 faces, 8 vertices, and 12 edges. The faces of the cube are square-shaped and each face meets at the right angle. Each of the faces meets the other four faces and one face is opposite. Each of the vertices meets the three faces and three edges. The edges and faces opposite to each other are parallel.

Types of Questions Asked from Cube Reasoning

There are several types of questions that have been seen from the topic cube -

1. Cutting of a cube and counting of smaller cubes

2. Counting of coloured cubes

Let’s discuss these types and cube reasoning tricks in detail with the help of examples -

1. Cutting of a Cube and Counting of Smaller Cubes

In these types of problems, a bigger cube is divided into smaller cubes by making the required number of cuts on different faces. Each smaller cube is of equal length.

To understand the concept, let’s assume that the bigger cube of length ‘L1’ is cut from different faces to form smaller cubes of length ‘L2’.

If we divide the length of a bigger cube by the length of the smaller cubes, we will get the number of parts (of each face) in which the cube is divided, and that is denoted by ‘n’.

∴ n = L1/L2

So, the total number of cuts to be made = 3 × (n - 1)

The total number of smaller cubes formed due to the division of a cube = (n)³

Example: Suppose a cube of length 27 cm is cut into smaller cubes of length 3 cm. How many cuts will be made and how many smaller cubes will be formed?

Answer: n = L1/L2 = 27/3 = 9

∴ Total number of cuts = 3 × (n - 1) = 3 × (9 - 1) = 3 × 8 = 24

∴ Total number of smaller cubes = (n)³ = (9)³ = 729

2. Counting of Coloured Cubes

In these types of problems, the given cube will be painted on all its surfaces with any colour. So, here, we have to find the number of coloured cubes based on the number of painted surfaces of smaller cubes. When we cut a painted cube to form smaller cubes, we will get different types of painted cubes based on the number of painted surfaces. We have two categories of coloured cubes:

(I) Single-Coloured Cube

Here, all the surfaces of the cube are painted with only one colour. When the cube is cut into smaller cubes, we will get different types of cubes on the basis of the number of painted surfaces. They are as follows:

Corner cube (3-Faces coloured) - When the painted cube is cut to form smaller cubes, the maximum number of the painted surfaces of smaller cubes can be 3. These types of cubes are formed at the corner of the bigger cube, that’s why, these cubes are also known as corner cubes. Thus, all the corner cubes are painted on 3 surfaces. As we know, there are a total of 8 corners.

So, the number of smaller cubes of which 3 surfaces are painted = 8

Middle cubes (2-Faces coloured) - When the painted cube is cut, the formed smaller cubes are also painted. These types of cubes are formed at the middle of the edges of the cube, that’s why, these cubes are also known as middle cubes.

The number of smaller cubes of which 2 surfaces are painted = 12 × (n - 2)

Central cubes (1-Face coloured) - When the painted cube is cut, the formed smaller cubes are also painted. These types of cubes are formed at the centre of the faces of the cube, that’s why, these cubes are also known as central cubes.

The number of smaller cubes of which 1 surface is painted = 6 × (n - 2)²

Inner Central cubes (0-Faces coloured) - When the painted cube is cut, the formed smaller cubes are also painted. These types of cubes are formed inside the centre of the cube, that’s why, these cubes are also known as inner central cubes.

The number of smaller cubes of which 0 surface is painted = (n - 2)³

Example: A bigger cube with all surfaces painted yellow is cut into 27 smaller cubes of equal size. How many smaller cubes are there which have 3 surfaces painted, 2 surfaces painted, 1 surface painted, and no surface painted?

Answer: Total smaller cubes = 27

⇒ (n)³ = 27 ⇒ n = 3

Total number of cubes with 3 surfaces painted = 8

Total number of cubes with 2 surfaces painted = 12 × (n - 2) = 12 × (3 - 2) = 12 × 1 = 12

Total number of cubes with 1 surface painted = 6 × (n - 2)² = 6 × (3 - 2)² = 6 × 1 = 6

Total number of cubes with 0 surfaces painted = (n - 2)³ = (3 - 2)³ = 1

(II) Multi-coloured Cube

Here, all the surfaces of the cube are painted with different colours. When the cube is cut into smaller cubes, we will get different types of cubes based on the number of painted surfaces. They are as follows:

Corner Cube (3-Faces coloured) - When the painted cube is cut to form smaller cubes, the maximum number of the painted surfaces of smaller cubes can be 3. These types of cubes are formed at the corner of the bigger cube, that’s why, these cubes are also known as corner cubes. Thus, all the corner cubes are painted on 3 surfaces. As we know, there are a total of 8 corners.

So, the number of smaller cubes of which 3 surfaces are painted = 8

But here, if we talk about the painted surfaces with a particular colour, then we can simply refer to the picture of the cube to identify the painted surface of the cube with a specific colour.

Middle Cubes (2-Faces coloured) - When the painted cube is cut, the formed smaller cubes are also painted. These types of cubes are formed at the middle of the edges of the cube, that’s why, these cubes are also known as middle cubes.

The number of smaller cubes of which 2 surfaces are painted = 12 × (n - 2)

But here, if we talk about the painted surfaces with a particular colour, then we can simply refer to the picture of the dice. 2-faces coloured cubes depend on the edges of the cube. Multiply (n - 2) by the number of required edges to identify the painted surfaces of the cube with a specific colour.

Central Cubes (1-Face coloured) - When the painted cube is cut, the formed smaller cubes are also painted. These types of cubes are formed at the centre of the faces of the cube, that’s why, these cubes are also known as central cubes.

The number of smaller cubes of which 1 surface is painted = 6 × (n - 2)²

But here, if we talk about the painted surfaces with a particular colour, then we can simply refer to the picture of the dice. 1-face coloured cubes depend on the faces of the cube. Multiply (n - 2)2 by the number of required faces to identify the painted surfaces of the cube with a specific colour.

Inner Central Cubes (0-Faces coloured) - When the painted cube is cut, the formed smaller cubes are also painted. These types of cubes are formed inside the centre of the cube, that’s why, these cubes are also known as inner central cubes.

The number of smaller cubes of which 0 surface is painted = (n - 2)³

Example: Two adjacent surfaces of a cube are painted red, two other adjacent faces are blue, and two remaining adjacent faces are painted green. Now it is cut into 125 smaller cubes, then how many smaller cubes have 2 surfaces painted with red and green colour, and 1 surface painted with blue colour?

Answer: Total smaller cubes = 125

⇒ (n)³ = 125 ⇒ n = 5

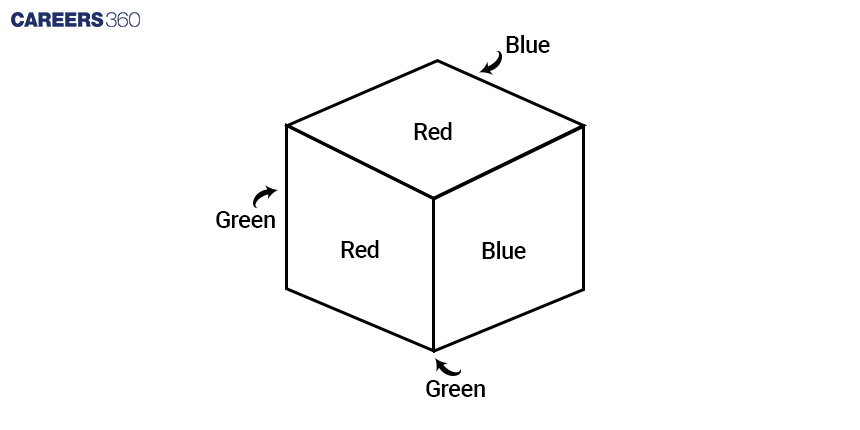
Total number of cubes with 2 surfaces painted (Red + Green), Here, if we check the figure, the edges that have red and green faces at their sides, there are only 3 such edges.

Thus, the total number of required cubes = 3 × (n - 2) = 3 × (5 - 2) = 3 × 3 = 9

Total number of cubes with 1 surface painted (Blue), here, if we check the figure, 2 faces that are painted blue.

Thus, the total number of required faces = 2 × (n - 2)² = 2 × (5 - 2)² = 2 × 9 = 18

The candidates who are preparing for the upcoming entrance and Government exams can also refer to the links given below and master the reasoning ability section:

Recommended Books and Online Resources

1. A Modern Approach to Verbal & Non-Verbal Reasoning by R.S. Aggarwal

2. SSC Reasoning by Rakesh Yadav

Question Weightage of Cube in Competitive Exams

The number of questions based on the cube varies from exam to exam -
1) Questions asked in SSC exams i.e. SSC MTS, SSC CGL, SSC CHSL, SSC CPO, Steno - 2 to 3 questions.
2) Questions asked in the RRB exam i.e. Group D, NTPC, JE, ALP etc - 2 to 3 questions.
3) Questions asked in Banking exams, Bank PO, Bank Clerk - 1 to 2 questions.
4) The candidates must practice cube reasoning questions pdf or questions on cube reasoning to ace the topic cube reasoning.

Note: Practice cube reasoning questions with answers of each type given below.

Practice Questions For Cutting of a Cube and Counting of Smaller Cubes

Q1. Directions: A bigger cube of length 64 cm is cut into smaller cubes of length 8 cm. What is the total number of cubes made?

A) 27

B) 125

C) 512 (Correct)

D) 64

Solution: Length of bigger cube = 64 cm, Length of each smaller cube = 8 cm

Thus, n = 64/8 = 8

So, the total number of cubes made = (n)³ = (8)3 = 512

Hence, the third option is correct.

Q2. Directions: A bigger cube is cut into 125 smaller cubes. How many cuts are required to form these smaller cubes?

A) 20

B) 5

C) 10

D) 12 (Correct)

Solution: The total number of cubes made = 125

⇒ (n)³ = 125 ⇒ n = 5

Total number of cuts = 3 × (n - 1) = 3 × (5 - 1) = 3 × 4 = 12

Hence, the fourth option is correct.

Q3. Directions: A bigger cube of length 48 cm is cut into smaller cubes of length 8 cm. What is the total number of cubes made?

A) 64

B) 216 (Correct)

C) 125

D) 40

Solution: Length of bigger cube = 48 cm, Length of each smaller cube = 8 cm

Thus, n = 48/8 = 6

So, the total number of cubes made = (n)³ = (6)³ = 216

Hence, the second option is correct.

Q4. Directions: If a number of smaller cubes are taken out from a bigger cube, each side is ¼ the size of the original cube’s side. What is the total number of smaller cubes made?

A) 60

B) 64 (Correct)

C) 25

D) 20

Solution: Let the length of the bigger cube = x cm and the length of each smaller cube = x/4 cm

Thus, n = x/(x/4) = 4

So, the total number of cubes made = (n)³ = (4)³ = 64

Hence, the second option is correct.

Q5. Directions: If a number of smaller cubes are taken out from a bigger cube, each side is 1/7 the size of the original cube’s side. What is the total number of smaller cubes made?

A) 343 (Correct)

B) 64

C) 125

D) 150

Solution: Let the length of the bigger cube = x cm, and the length of each smaller cube = x/7 cm

Thus, n = x/(x/7) = 7

So, the total number of cubes made = (n)³ = (7)³ = 343

Hence, the first option is correct.

Practice Questions For Counting of Coloured Cubes

Q1. A 12 cm coloured cube is cut into 2 cm smaller cubes. How many cubes have 2 surfaces painted and 1 surface painted?

A) 48, 96 (Correct)

B) 48, 90

C) 56, 96

D) 36, 94

Answer: Length of original cube = 12 cm, Length of smaller cubes = 2 cm

So, n = 12/2 = 6

Total number of cubes with 2 surfaces painted = 12 × (n - 2) = 12 × (6 - 2) = 12 × 4 = 48

Total number of cubes with 1 surface painted = 6 × (n - 2)² = 6 × (6 - 2)² = 6 × 16 = 96

Hence, the first option is correct.

Q2. A 25 cm coloured cube is cut into 5 cm smaller cubes. How many cubes have 3 surfaces painted, 2 surfaces painted and 1 surface painted?

A) 8, 24, 54

B) 8, 36, 45

C) 8, 36, 54 (Correct)

D) 8, 48, 36

Answer: Length of original cube = 25 cm, Length of smaller cubes = 5 cm

So, n = 25/5 = 5

Total number of cubes with 3 surfaces painted = 8

Total number of cubes with 2 surfaces painted = 12 × (n - 2) = 12 × (5 - 2) = 12 × 3 = 36

Total number of cubes with 1 surface painted = 6 × (n - 2)² = 6 × (5 - 2)² = 6 × 9 = 54

Hence, the third option is correct.

Q3. A bigger cube with all surfaces painted yellow is cut into 27 smaller cubes of equal size. How many cubes are there which have only one surface painted?

A) 1

B) 6 (Correct)

C) 8

D) 10

Solution: Total number of smaller cubes = 27

⇒ Total number of smaller cubes = (n)³ ⇒ (n)³ = 27 ⇒ n = 3

Total number of cubes with 1 surface painted = 6 × (n - 2)2 = 6 × (3 - 2)² = 6 × 1 = 6

Hence, the second option is correct.

Q4. A cube of white material is painted black on all its surfaces. If it is cut into 216 smaller cubes of the same size, then how many cubes will have 2 surfaces painted black?

A) 96

B) 56

C) 64

D) 48 (Correct)

Solution: Total number of smaller cubes = 216

⇒ Total number of smaller cubes = (n)³ ⇒ (n)³ = 216 ⇒ n = 6

Total number of cubes with 2 surface painted = 12 × (n - 2) = 12 × (6 - 2) = 12 × 4 = 48

Hence, the fourth option is correct.

Q5. A coloured cube is cut into 343 smaller cubes of the same size, then how many cubes will have at least 2 surfaces painted?

A) 48

B) 68 (Correct)

C) 8

D) 40

Solution: Total number of smaller cubes = 343

⇒ Total number of smaller cubes = (n)³ ⇒ (n)³ = 343 ⇒ n = 7

Total number of cubes with at least 2 surfaces painted = Cubes with 2 surfaces painted + Cubes with 3 surfaces painted = (12 × (n - 2)) + 8 = (12 × (7 - 2)) + 8 = (12 × 5) + 8 = 60 + 8 = 68

Hence, the second option is correct.

Q6. A coloured cube is cut into 125 smaller cubes of the same size, then how many cubes will have at most 2 surfaces painted?

A) 117 (Correct)

B) 124

C) 96

D) 105

Solution: Total number of smaller cubes = 125

⇒ Total number of smaller cubes = (n)³ ⇒ (n)³ = 125 ⇒ n = 5

Total number of cubes with at most 2 surfaces painted = Cubes with 2 surfaces painted + Cubes with 1 surfaces painted + Cubes with no surface painted = (12 × (n - 2)) + (6 × (n - 2)2) + ((n - 2)3) = (12 × (5 - 2)) + (6 × (5 - 2)2) + ((5 - 2)3) = (12 × 3) + (6 × 9) + (27) = 117

Hence, the first option is correct.

Q7. There is a bigger cube of 12 cm. 2 adjacent surfaces of it are painted red, 2 other adjacent surfaces are painted yellow, 1 surface is painted blue, and 1 surface is painted green. Now it is cut into smaller cubes of 2 cm, then how many smaller cubes are there which have only 2 surfaces painted with red and blue colour?

A) 48

B) 8 (Correct)

C) 24

D) 32

Solution: Length of bigger cube = 12 cm, Length of smaller cube = 2 cm

So, n = 12/2 = 6

Now, we have to consider the smaller cubes whose one surface is painted red and the other is painted blue, as shown in the diagram below:

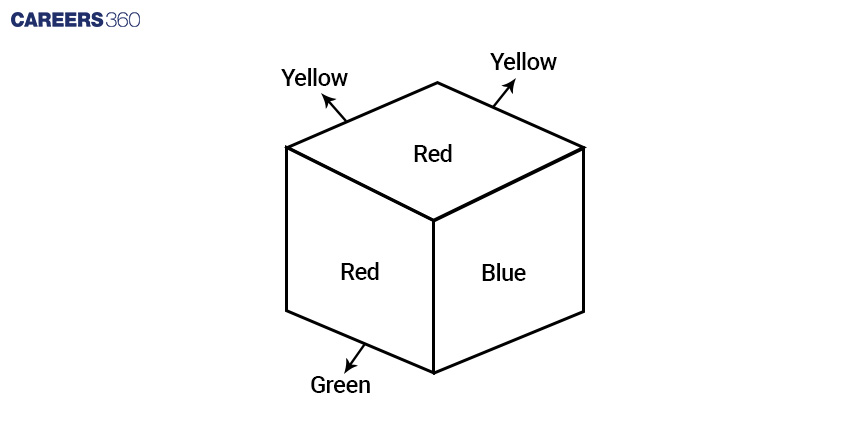
So, according to the above diagram, there are only 2 such edges where these required cubes are formed.

The number of smaller cubes which have only 2 surfaces painted with red and blue colour = 2 × (n - 2)

= 2 × (6 - 2) = 2 × 4 = 8

Hence, the second option is correct.

Q8. A bigger coloured cube is cut into 125 smaller cubes of 8 cm3, then what is the length of the bigger cube?

A) 40 cm

B) 20 cm

C) 5 cm

D) 10 cm (Correct)

Solution: Total number of smaller cubes = 125

The total number of smaller cubes = (n)³ ⇒ (n)³ = 125 ⇒ n = 5

The volume of each smaller cube = 8 cm3

So, the length of the smaller cube = 2 cm

Let the length of the bigger cube be L cm.

So, n = L/2 ⇒ 5 = L/2 ⇒ L = 10 cm

Hence, the fourth option is correct.

Q9. Two adjacent surfaces of a bigger cube are painted red, 1 surface is painted blue and the remaining 3 surfaces are painted yellow. Now, it is cut into 216 smaller cubes. How many smaller cubes have only 1 surface painted with a yellow colour?

A) 48 (Correct)

B) 32

C) 16

D) 12

Solution: Total number of smaller cubes = 216

The total number of smaller cubes = (n)³ ⇒ (n)³ = 216 ⇒ n = 6

Here, we have to determine the number of smaller cubes that have 1 surface painted with yellow colour.

Yellow painted surfaces are 3,

The number of cubes that have only 1 surface painted with yellow colour = 3 × (n - 2)² = 3 × (6 - 2)² = 3 × 16 = 48

Hence, the first option is correct.

Q10. Four surfaces of a bigger cube are painted red, and the remaining 2 surfaces are painted yellow. Now, it is cut into 64 smaller cubes. How many smaller cubes have only 1 surface painted with a red colour?

A) 8

B) 32

C) 16 (Correct)

D) 12

Solution: Total number of smaller cubes = 64

The total number of smaller cubes = (n)³ ⇒ (n)³ = 64 ⇒ n = 4

Here, we have to determine the number of smaller cubes that have 1 surface painted with red colour.

Red painted surfaces are 4,

The number of cubes that have only 1 surface painted with red colour = 4 × (n - 2)² = 4 × (4 - 2)² = 4 × 4 = 16

Hence, the third option is correct.

Read more: For verbal reasoning read the topics below:

About the Faculty
Tanu Gupta, with over a decade of experience as a reasoning faculty, specializes in preparing students for various entrance examinations and career development. Her extensive work with multiple educational platforms and institutions has honed her expertise in logical and analytical thinking. Her dedication to innovative teaching methods ensures these articles provide practical insights and expert guidance.