Logical Deductions and Connections: Meaning, Questions, Formula, Examples

Logical deduction is an important topic in analytical reasoning. In easy words, logical deductions meaning identifying patterns, examining evidence and drawing conclusions from the given premises or statements. This skill is useful in many aspects of life such as making decisions in any situation, solving problems or solving tricky puzzles.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: IBSAT 2024 Mock Tests | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

Question with Solutions: Missing Number | Alphabet Test | Arithmatical Problems | Calendar

This Story also Contains

1. Logical Deduction Introduction
2. Tips and Tricks to solve the Syllogism questions
3. Example Problems on Logical Deductions Based Relational Questions

Logical Deduction Introduction

Logical dedication requires rational thinking, to arrive at correct and relatable conclusions. Whether you are solving logical deductions, any mathematical problem or have to decide something important at the workplace or any other place logical reasoning is a precious skill. Logical deductions and connections questions are mostly seen in the UGC NET, CAT, CLAT, Banking etc exams. Logical deductions solving requires the complete understanding of the concept. These questions consist of good weightage such as 3-5 marks depending on the level of the exam. It is of two types.

1) Immediate Deductive Inference

2) Mediate Deductive Inference

Let’s discuss the types and logical deductions rules in detail-

Immediate Deductive Inference

Immediate deductive inference is inference in which a conclusion is drawn from only one premise. It involves two propositions one is premise and the other is conclusion. There are three immediate deductive inferences which are as follows:
1) Conversion: In this inference subject and predicate are interchanged.
For example - The conversion of “Some women are believers.” is “Some believers are women”.
2) Obversion: In this inference to form the obverse of a proposition, change the proposition's position and put back the predicate by its complement.
For example - The obverse of “All human beings are mortal.” is “No human being is immortal.”
3) Contraposition: The subject and predicate complement terms are interchanged in this inference. The contraposition of the proposition is done mainly in three parts such as firstly obverting the original, secondly, converting the resulting proposition and in the third step obverting the resultant one.
For example - The proposition “ All men are mortal” obverts to “ No men are immortal” which converts to “No non-mortal (immortal) men are human” which when obverted gives “All non-mortal are non-men.”

Example:
It is an inference which can be made from only one premise, statement or proposition.

Statement: All frogs are green.
Immediate Inference: No frogs are not green or no frogs are non-green.

Mediate Deductive Inference

Mediate deductive inference is inference in which a conclusion is drawn from two or more premises. Both premises together implicit the conclusion.
It consists of three main parts which are as follows:
1) Major Premise
2) Minor Premise
3) Conclusion

In general, the central premise is a statement considered true.
Syllogism is a form of mediate deductive inference, in which the conclusion is drawn from two premises taken jointly.
Example:
Statements:
1) All men are handsome. (Major premise)
2) Ramesh is a man. (Minor premise)
Conclusion:
Ramesh is handsome.
Solution:
Ramesh is a man.
The minor premise is defined as a definite example of the major premise.

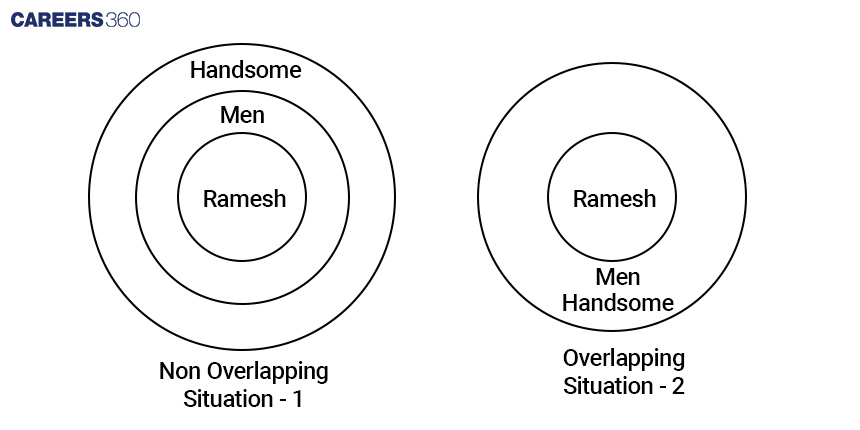
The above Venn diagrams represent the combination of major and minor statements in two different ways. In the first situation, the statement “All men are handsome”, the Venn diagram of men is inside the Venn diagram of handsome. Hence, the major statement is true. And since Ramesh is a man, the Venn diagram representing Ramesh should be inside the circle of Men. In the second case, the only difference is the major statement “All men are handsome”, the Venn diagrams of men and handsome overlap with each other. Because that’s another possibility. Since Ramesh is a man, it is represented inside the circle of Men. Observing both situations, you should agree that the conclusion given “Ramesh is handsome” is true in both situations.

Logical Deductions trick or Point to remember: The conclusion should be true according to all the possible cases. One should draw all possible cases before concluding.

Example:
Directions: In the following question, two statements are given, followed by a conclusion. You have to consider the statements to be true even if they are seen to be at variance from commonly known facts. You have to decide whether a conclusion is correct or incorrect following the given statements.

Major premise: All Teachers are left-handed.

Minor premise: All left-handed are Doctors.

The conclusion is that some Doctors are Teachers.

A. Correct

B. Incorrect

Solution:
The Venn diagram is given below according to the given statements:

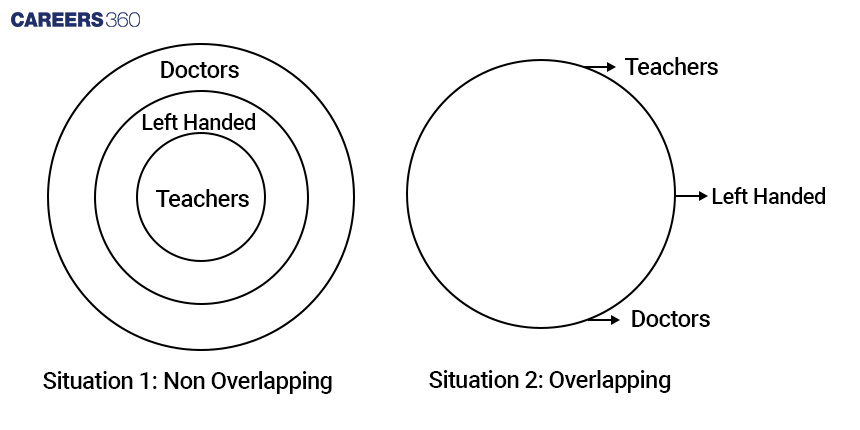
Situation 1:
The Venn diagram of teachers is inside left-handed which in turn is inside the Venn diagram of doctors. According to the diagram, the Venn diagram of teachers overlaps with the Venn diagram of doctors indicating that some doctors are teachers. Hence the conclusion is correct according to this diagram, but can not be concluded as the final answer until the second case is checked.
Situation 2:
Since all the Venn diagrams overlap with each other, according to the diagram all the doctors are teachers or all the teachers are doctors. Hence, the conclusion is “some doctors are teachers” is wrong. Since the conclusion is wrong according to the second Venn diagram. So, the conclusion is incorrect. Hence, the second option is correct.

Four-Fold Classification of Proposition

According to quality, propositions are classified as Affirmative and Negative whereas according to quantity, propositions are classified into universal and particular.

Based on the above two principles, there are four types of propositions which are as follows:
(1) Universal affirmative (A)
(2) Universal negative (E)
(3) Particular affirmative (I)
(4) Particular negative (O).
These propositions are called unconditional or categorical propositions because no condition is stated anywhere in the propositions. Hence, this is known as a four-fold classification of propositions.

Example: Using the X variable to represent the subject and the Y variable to represent the predicate, the four types of categorical propositions are A-propositions, where all X are Y; E propositions, where all X are not Y; I propositions, where some X are Y; and O proposition, where some X are not Y.

Distribution of terms in A, E, I, O propositions

1) A term is said to be distributed when the reference is given to both the subject term and predicate term.
2) In A proposition SUBJECT is DISTRIBUTED and the PREDICATE is UNDISTRUBUTED.
3) In E proposition SUBJECT is DISTRIBUTED and the PREDICATE is also DISTRIBUTED.
4) In I proposition SUBJECT is UNDISTRIBUTED and the PREDICATE is also UNDISTRIBUTED.
5) In O proposition SUBJECT is UNDISTRIBUTED and the PREDICATE is DISTRIBUTED.

Example:
Given below are four propositions. Two of them are related in such a way that they are not true and they may be false. You have to select the code to state those two propositions.
(1) All women are honest.
(2) No women are honest.
(3) Some women are honest.
(4) Some women are not honest.
You have to choose the correct answer from the options given below:
(1) 1 and 2 only
(2) 2 and 3 only
(3) 3 and 4 only
(4) 1 and 4 only
Solution:
(1) All women are honest - Universal affirmative.
(2) No women are honest - Universal negative.
(3) Some women are honest - Partial affirmative.
(4) Some women are not honest - Partial negative.
Only (1) and (2) are forming complementary pairs. Universal affirmative and universal negative form complementary pairs. Therefore, they can’t occur together. Hence, the first option is correct.

Tips and Tricks to solve the Syllogism questions

(1) First, read the statements and conclusions carefully and pay attention to words like ‘some’, ‘very few’, ‘all’, ‘at least’, etc. These words form the base to solve the syllogism questions.

(2) The best way to solve syllogism questions is to draw the Venn diagrams. This will make the explanation more clear and simplified.

(3) Never assume anything from the outer world while solving the syllogism questions. The only information that has to be followed while solving the question is the information mentioned in the question. You should not assume anything while solving questions.

(4) In the end, analyse the Venn diagram's conclusion and check for other alternative solutions to mark the answer.

Learn more: The verbal reasoning topics are given below.

Example Problems on Logical Deductions Based Relational Questions

1. Directions: In the following question, two statements are given, followed by two conclusions, I and II. You have to consider the statements to be true even if they are seen to be at variance from commonly known facts. You have to decide which of the given conclusions, if any, follows from the given statements.

Statements:
All cats are mammals.
Some mammals are dogs.

Conclusions:
All cats are dogs.
Some dogs are cats.

1. Only conclusion I follows

2. Only conclusion II follows

3. Either I or II follows

4. Neither I nor II follows

5. Both I and II follow

Solution:

According to the given statements, the premises establish that cats are mammals, but they do not establish a direct relationship between cats and dogs. Therefore, neither of the conclusions can be logically deduced from the given statements. Hence, the fourth option is correct.

2. Directions: In the following question, two statements are given, followed by two conclusions, I and II. You have to consider the statements to be true even if they are seen to be at variance from commonly known facts. You have to decide which of the given conclusions, if any, follows from the given statements.

Statements:
If it is cold, people wear sweaters.
People are wearing sweaters.

Conclusions:
It is cold.
If people are wearing sweaters, it is cold.

1. Only conclusion I follows

2. Only conclusion II follows

3. Either I or II follows

4. Neither I nor II follows

5. Both I and II follow

Solution:
According to the given statements, the first conclusion follows because if people are wearing sweaters, it implies that it is cold (based on the first premise). The second conclusion restates the conditional relationship established in the first premise. Hence, the fifth option is correct.

3. Directions: In the following question, two statements are given, followed by two conclusions, I and II. You have to consider the statements to be true even if they are seen to be at variance from commonly known facts. You have to decide which of the given conclusions, if any, follows from the given statements.

Statements:
Some teachers are fools.
Some fools are poor.

Conclusions:
Some teachers are poor.
Some poor are teachers.

1. Only conclusion I follows

2. Only conclusion II follows

3. Either I or II follows

4. Neither I nor II follows

5. Both I and II follow

Solution:
Here, both premises are particular, and no definite conclusion follows. Hence, the fourth option is correct.

4. Directions: In the following question, two statements are given, followed by two conclusions, I and II. You have to consider the statements to be true even if they are seen to be at variance from commonly known facts. You have to decide which of the given conclusions, if any, follows from the given statements.

Statements:
Some kings are queens.
All queens are beautiful.

Conclusions:
All kings are beautiful.
All queens are kings.

1. Only conclusion I follows

2. Only conclusion II follows

3. Either I or II follows

4. Neither I nor II follows

5. Both I and II follow

Solution:
Here, one premise is particular. Therefore, the conclusion must be particular. So, neither I nor II follows. Hence, the fourth option is correct.

5. Directions: In the following question, two statements are given, followed by two conclusions, I and II. You have to consider the statements to be true even if they are seen to be at variance from commonly known facts. You have to decide which of the given conclusions, if any, follows from the given statements.

Statements:
1. All dawns are day.
2. No day is night.

Conclusions:
I. No night is day.
II. Some dawns are night.

1) Only conclusion I follows

2) Only conclusion II follows

3) Both I and II follow

4) Neither I nor II follows

Solution:

The possible Venn diagram according to the given statements is as follows –

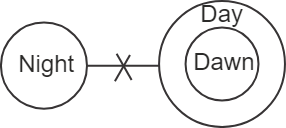
Let's analyse the conclusions –

Conclusion (I): No night is day – From the diagram, we can see that circles representing night and day have a negative relation between them. So, this conclusion follows.

Conclusion (II): Some dawns are night – From the diagram, we can see that circles representing night and day have a negative relation between them and dawn is the part of day, which implies that no dawn is night. So, this conclusion does not follow.

So, the only conclusion I follows. Hence, the first option is correct.

6. Directions: In the following question two statements are given, followed by two conclusions I and II. You have to consider the statements to be true even if they are seen to be at variance from commonly known facts. You have to decide which of the given conclusions, if any follows from the given statements.

Statements:
I. All flowers are leaves.
II. Some flowers are plants.

Conclusions:
I. Some leaves are plants.
II. Some plants are flowers.

1) Only conclusion I follows

2) Only conclusion II follows

3) Both I and II follow

4) Neither I nor II follows

Solution:
The possible Venn diagram according to the given statements is as follows –

Let's analyse the conclusions –

Conclusion (I): Some leaves are plants – From the diagram, we can see that some parts of the circles that represent plants and leaves intersect each other and have some common area between them, which means that some leaves are plants is a true conclusion.

Conclusion (II): Some plants are flowers – From the diagram, we can see that some parts of the circles that represent plants and flowers intersect each other and have some common part between them, which means that some plants are flowers is a true conclusion.

Therefore, both conclusions I and II follow is the correct answer. Hence, the third option is correct.

7. Directions: In the following question two statements are given, followed by two conclusions I and II. You have to consider the statements to be true even if they are seen to be at variance from commonly known facts. You have to decide which of the given conclusions, if any follows from the given statements.

Statements:
I. All clouds are fogs.
II. All fogs are white.

Conclusions:
I. Some white are clouds.
II. Some fogs are clouds.

1) Only conclusion I follows

2) Only conclusion II follows

3) Both I and II follow

4) Neither I nor II follows

Solution:
The possible Venn diagram according to the given statements is as follows –

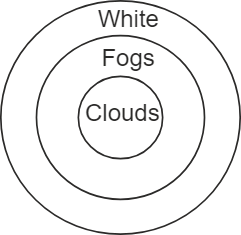
Now, let's analyse the conclusions –

Conclusion (I): Some white are clouds – From the diagram, we can see that the circle of clouds is completely inside the circle of white. Therefore, some white are clouds is a true conclusion.

Conclusion (II): Some fogs are clouds – From the diagram, we can see that the circle of clouds is completely inside the circle of white. Therefore, some fogs are clouds is a true conclusion.

Therefore, both conclusions I and II follow. Hence, the third option is correct.

8. Directions: In the following question two statements are given, followed by two conclusions I and II. You have to consider the statements to be true even if they are seen to be at variance from commonly known facts. You have to decide which of the given conclusions, if any follows from the given statements.

Statements:
If it is night, it is dark outside.
It is dark outside.

Conclusions:
It is night.
If it is dark outside, it is night.

1. Only conclusion I follows

2. Only conclusion II follows

3. Either I or II follows

4. Neither I nor II follows

5. Both I and II follow

Solution:
Both conclusions logically follow from the given premises. The first conclusion follows because if it is dark outside, it implies that it is night (based on the first premise). The second conclusion sums up the conditional relationship established in the first premise. Hence, the fifth option is correct.

9. Directions: In the following question two statements are given, followed by two conclusions I and II. You have to consider the statements to be true even if they are seen to be at variance from commonly known facts. You have to decide which of the given conclusions, if any follows from the given statements.

Statements:
All students who study regularly pass exams.
Randeep studies regularly.

Conclusions:
Randeep is a student.
Randeep will pass the exams.

1. Only conclusion I follows

2. Only conclusion II follows

3. Either I or II follows

4. Neither I nor II follows

5. Both I and II follow

Solution:
The first conclusion logically follows from the given premises because if all students who study regularly pass exams, and Randeep studies regularly, then Randeep must be a student. The second conclusion also follows logically because, according to the premises, if Randeep is a student who studies regularly, he will pass exams. Hence, the fifth option is correct.

10. Directions: In the following question, two statements are given followed by two conclusions I and II. You have to consider the two statements to be true even if they seem to be at variance from commonly known facts. You have to decide which of the given conclusions, if any, follow from the given statements.

Statements:
1. All men are prisoners.
2. No prisoners are educated.

Conclusions:
I. All prisoners are educated.
II. No men are educated.

1) Only conclusion I follows

2) Only conclusion II follows

3) Neither I nor II follows

4) Both Conclusion I and Conclusion II follow

Solution:

The possible Venn diagram according to the given statements is as follows –

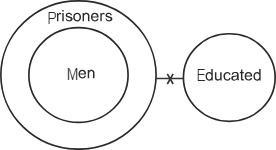
Let's analyse the conclusions –

Conclusion (I): All prisoners are educated – From the Venn diagram, we can see that none of the prisoners are educated as there is no overlap. So, this conclusion does not follow.

Conclusion (II): No men are educated – From the Venn diagram, we can see that none of the prisoners are educated and the circle of men lies inside the circle of prisoners. So, from this, it can be inferred that if no prisoners are educated then no men are educated. Thus, this conclusion follows.

So, only conclusion II follows. Hence, the second option is correct.

11. Directions: In the following question below, some statements are followed by some conclusions. Taking the given statements to be true, even if they seem to be at variance from commonly known facts, read all the conclusions and then decide which of the given conclusions logically follows from the given statements.

Statements:
Some bags are hot.
All hot things are cakes.

Conclusions:
I. All cakes are bags.
II. All bags are cakes.

1) Conclusion I follows

2) Conclusion II follows

3) Neither I nor II follows

4) Both I and II follow
Solution:

The possible Venn diagram according to the given statements is as follows –

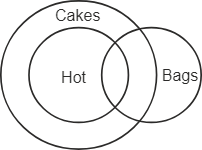
Let's analyse the conclusions –

Conclusion (I): All cakes are bags – From the Venn diagram, the circle of the cake is not completely inside the circle of the bag only some parts of cakes and bags intersect and have a common area between them. This means that some cakes are bags. So, this conclusion does not follow.

Conclusion (II): All bags are cakes – From the Venn diagram, the circle of the bag is not completely inside the circle of the cake only some parts of cakes and bags intersect and have a common area between them. This means that some bags are cakes. So, this conclusion does not follow.

So, neither I nor II follows. Hence, the third option is correct.

12. Directions: In the following question, two statements are given followed by two conclusions I and II. You have to consider the two statements to be true even if they seem to be at variance from commonly known facts. You have to decide which of the given conclusions, if any, follow from the given statements.

Statements:
I. Sohan is a good sportsman.
II. Sportsmen are healthy.

Conclusions:
I. All healthy people are sportsmen.
II. Sohan is healthy.

1) Conclusion I follows

2) Conclusion II follows

3) Neither Conclusion I nor Conclusion II follows

4) Both Conclusion I and Conclusion II follow

Solution:

The possible Venn diagram according to the given statements is as follows –

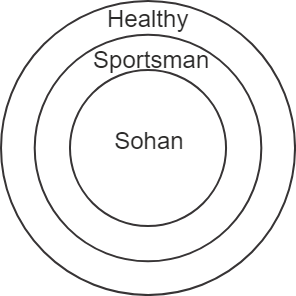
Let's analyse the conclusions –
Conclusion (I): All healthy people are sportsmen – From the Venn diagram, the circle of sportsmen is completely inside the circle of healthy. Therefore, some healthy people are sportsmen is correct but all healthy people are sportsmen is a false conclusion.

Conclusion (II): Sohan is healthy – From the Venn diagram, the circle that represents Sohan lies completely inside the circle that represents healthy. So, this conclusion follows.

Thus, only conclusion II follows. Hence, the second option is correct.

13. Directions: In the following question below, some statements are followed by some conclusions. Taking the given statements to be true, even if they seem to be at variance from commonly known facts, read all the conclusions and then decide which of the given conclusions logically follows from the given statements.

Statements:
I. All dogs are bullocks.
II. All bullocks are goats.

Conclusions:
I. All dogs are goats.
II. All goats are dogs.

1) Conclusion I follows

2) Conclusion II follows

3) Neither Conclusion I nor Conclusion II follows

4) Both Conclusion I and Conclusion II follow

Solution:

The possible Venn diagram according to the given statements is as follows –

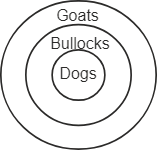
Let's analyse the conclusions –

Conclusion (I): All dogs are goats – From the Venn diagram, we can see that the circle that represents dogs lies completely inside the circle that represents goats. This means that all the dogs are goats. So, this conclusion follows.

Conclusion (II): All goats are dogs – From the Venn diagram, we can see that the circle of dogs completely lies inside the circle of goats, implying that some goats are dogs. So, this conclusion does not follow. So, the only conclusion I follows. Hence, the first option is correct.

14. Directions: In the following question below, some statements are followed by some conclusions. Taking the given statements to be true, even if they seem to be at variance from commonly known facts, read all the conclusions and then decide which of the given conclusions logically follows from the given statements.

Statements:
1. All young girls are modern.
2. No modern men are superstitious.

Conclusions:
I. No girls are superstitious.
II. No young men are superstitious.

1) Conclusion I follows

2) Conclusion II follows

3) Neither Conclusion I nor Conclusion II follows

4) Both Conclusion I and Conclusion II follow

Solution:

The possible Venn diagram according to the given statements is as follows –

Let's analyse the conclusions –

Conclusion (I): No girls are superstitious – The statements only mention young girls. None of the statements contain any information about girls. So, this conclusion does not follow.

Conclusion (II): No young men are superstitious – The statements only mention modern men. None of the statements contain any information about young men. So, this conclusion does not follow.

So, neither Conclusion I nor Conclusion II follows. Hence, the third option is correct.

15. Directions: In the following question below are given some statements followed by some conclusions. Taking the given statements to be true even if they seem to be at variance from commonly known facts, read all conclusions and then decide which of the given conclusions logically follows from the given statements.

Statements:
Some black are red.
Some red are cups.
Some cups are plates.

Conclusions:
I. All black are cups.
II. Some black are plates.
III. No black is a plate.

1) Both I and II

2) Only III

3) All conclusions follow

4) None follows

Solution:

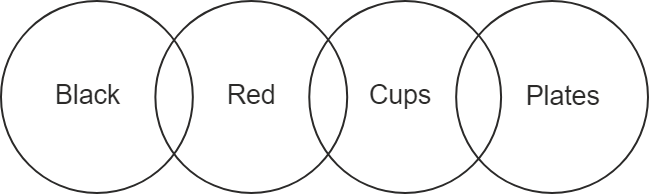
The Venn diagram is as follows –

Let's analyse the conclusions –

Conclusion (I): All black are cups – From the Venn diagram, there is no direct relation between black and cup. So, no definite relation can be drawn between them. Therefore, this conclusion does not follow.

Conclusion (II): Some black are plates – From the Venn diagram, there is no direct relation between black and plate. So, no definite relation can be drawn between them. Therefore, this conclusion does not follow.

Conclusion (III): No black is a plate – From the Venn diagram, there is no direct relation between black and plate. So, no definite relation can be drawn between them. Therefore, this conclusion does not follow.

So, none of the conclusions follows. Hence, the fourth option is correct.

16. Directions: In the following question below are given some statements followed by some conclusions. Taking the given statements to be true even if they seem to be at variance from commonly known facts, read all conclusions and then decide which of the given conclusions logically follows from the given statements.

Statements:
I. Some cups are plates.
II. No cup is a pencil.

Conclusions:
I. No plate is a pencil.
II. Some plates are pencils.
III. Some pencils are cups.

1) Only I

2) Only II

3) Both I and II

4) No conclusion follows

Solution

The Venn diagram is as follows –

Let's analyse the conclusions –

Conclusion I: No plate is a pencil – From the above Venn diagram, it is evident that there is no direct relation between the plate and the pencil. So, no definite relation can be drawn between them. Therefore, this conclusion does not follow.

Conclusion II: Some plates are pencils – From the above Venn diagram, it is evident that there is no direct relation between the plate and the pencil. So, no definite relation can be drawn between them. Therefore, this conclusion does not follow.

Conclusion III: Some pencils are cups – From the above Venn diagram, it is evident that there is a direct negative relation between pencils and cups. So, no positive relation can be drawn. Therefore, this conclusion does not follow.

17. Directions: In the following question below, some statements are followed by some conclusions. Taking the given statements to be true, even if they seem to be at variance from commonly known facts, read all the conclusions and then decide which of the given conclusions logically follows from the given statements.

Statements:
All plates are pens.
Some pens are pencils.

Conclusions:
I. All the plates are pencils.
II. No plate is a pencil.
III. Some pencils are pens.

1) Only I

2) Only II

3) Only III

4) Both I and III

Solution

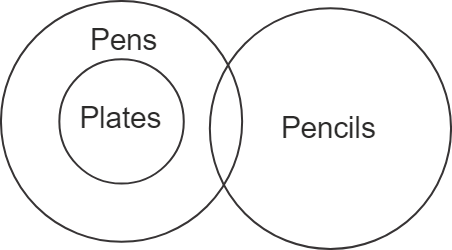
The Venn diagram is as follows –

Let's analyse the conclusions –

Conclusion (I): All plates are pencils – From the above Venn diagram, it is evident that there is no direct relation between plates and pencils. So, no definite relation can be drawn between them. Therefore, this conclusion does not follow.

Conclusion (II): No plate is pencil – From the above Venn diagram, it is evident that there is no direct relation between plates and pencils. So, no definite relation can be drawn between them. Therefore, this conclusion does not follow.

Conclusion (III): Some pencils are pens – From the above Venn diagram, it is evident that the circles representing pencils and pens overlap each other and have a part of their areas in common. So, this conclusion follows. So, only conclusion III follows. Hence, the third option is correct.

18. Directions: In the following question, two statements are given, followed by two conclusions, I and II. You have to consider the statements to be true even if they are seen to be at variance from commonly known facts. You have to decide which of the given conclusions, if any, follows from the given statements.

Statements:
All birds can fly.
Parrots are birds.

Conclusions:
Parrots can fly.
Some birds can run.

1. Only conclusion I follows

2. Only conclusion II follows

3. Either I or II follows

4. Neither I nor II follows

5. Both I and II follow

Solution:
The first conclusion can be logically deduced because the premises state that all birds can fly in the second statement it's given that parrots are birds. Therefore, this conclusion is true. The second conclusion cannot be deduced either because the premises do not provide information about swimming. Hence, the first conclusion is true.

19. Directions: In the following question, two statements are given, followed by two conclusions, I and II. You have to consider the statements to be true even if they are seen to be at variance from commonly known facts. You have to decide which of the given conclusions, if any, follows from the given statements.

Statements: All leaders are public speakers.
Some public speakers are teachers.

Conclusions:
All leaders are teachers.
Some teachers are leaders.

1. Only conclusion I follows

2. Only conclusion II follows

3. Either I or II follows

4. Neither I nor II follows

5. Both I and II follow

Solution:
The first conclusion cannot be logically deduced because the premises establish that all leaders are public speakers, but they do not provide information about teachers. The second conclusion cannot be deduced either because the premises state that some public speakers are teachers, but they do not establish a relationship between teachers and leaders. Therefore, none of the conclusions follows. Hence, the fourth option is correct.

20. Directions: In the following question, two statements are given, followed by two conclusions, I and II. You have to consider the statements to be true even if they are seen to be at variance from commonly known facts. You have to decide which of the given conclusions, if any, follows from the given statements.

Statements: No rat is man.
Some men are residents.

Conclusions:
Some rats are not residents.
Some men are rats.

1. Only conclusion I follows

2. Only conclusion II follows

3. Either I or II follows

4. Neither I nor II follows

5. Both I and II follow
Solution:
The first conclusion cannot be logically deduced because the premises state that no reptile is man, but they do not provide information about the relationship between rats and residents. The second conclusion cannot be deduced either because the premises establish that some men are residents, but they do not provide information about rats. Therefore, none of the conclusions follows. Hence, the fourth option is correct.

Note: Revise the solved examples repeatedly to learn how to solve logical deductions questions.

For non verbal reasoning read the topics below: