Number Series: Tricks & Solved Number Series Reasoning Questions

Number Series: Number Series is an important reasoning topic that is asked in various competitive and entrance exams such as banking, SSC, RRB, CUET, TANCET, BITSAT, VITEEE, APICET, KMAT, and JIPMAT exams. Generally, number series are asked in the form of a missing number. But nowadays it has been seen that the wrong number series questions are mostly asked in the exams. This wrong number series is an advanced pattern of missing numbers. If the candidates know the basics of the number series, then it will be easier for them to solve the wrong number series. This article will help the candidate understand the number series, its types and the wrong number series in detail.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: IBSAT 2024 Mock Tests | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

Question with Solutions: Missing Number | Alphabet Test | Arithmatical Problems | Calendar

This Story also Contains

1. What is Number Series Reasoning?
2. Types of Number Series in Reasoning
3. How to Solve the Number Series Quickly?
4. Tips and Number Series Reasoning Tricks
5. Solved Number Series Questions of Each Type
6. Practice and Resources
7. Question Weightage of Number Series in Competitive Exams
8. Number Series Reasoning Questions for Practice
9. Wrong Number Series Reasoning Questions for Practice
10. Number Series Questions for Bank Exams
11. Number Series Questions for Competitive Exams and Entrance Exams
12. Number Series Questions for VITEEE Exam

What is Number Series Reasoning?

The number series is defined as the arrangement of numbers in a definite order, and in which some numbers are missing or some numbers are wrongly placed in the series is called a number series. In the missing number series candidates need to find the missing number and in the wrong number series candidates need to identify the wrong number in the series. To find the missing number or wrong number candidates need to identify the pattern followed in the series to find the term of the series. There is no set pattern of a number series reasoning and each question follows a different type of pattern which candidates need to identify using their reasoning skills. There are various types of questions asked in the exams based on them we have classified the number series into different types.

Types of Number Series in Reasoning

There are many types of number series which are discussed below:

1. Increasing/ Addition number series: In this type of number series, numbers based on a specific pattern are added to get the next number. The added numbers can be consecutive even numbers, odd numbers, squares, cubes or multiples of any number depending on the series.

2. Decreasing/ Subtraction number series: In this type of number series, numbers based on a specific pattern are subtracted to get the next number. The subtracted numbers can be consecutive even numbers, odd numbers, squares, cubes or multiples of any number depending on the series.

3. Multiplication number series: In this type of number series, numbers based on a specific pattern are multiplied to get the next number. The multiplied numbers can be consecutive natural numbers, even numbers, odd numbers or multiples of a particular number depending on the series.

4. Division Number Series: In this type of number series, numbers based on a specific pattern are divided to get the next number. The number divided by the numbers in the series can be consecutive natural numbers, even numbers, odd numbers or a particular number depending on the series.

5. Square Number Series: In this type of number series, perfect squares are given and candidates need to find the missing square. The squares of the numbers which are given can be squares of consecutive numbers, even numbers, odd numbers etc.

6. Cube Number Series: In this type of number series, perfect cubes are given and candidates need to find the missing square. The cubes of the numbers which are given can be squares of consecutive numbers, even numbers, odd numbers etc.

7. Ascending/ Descending Number Series: In this type of number series, candidates are required to rearrange the numbers to find out the required number.

8. Mixed Number Series: In this type of number series, multiple mathematical operators such as addition, subtraction, multiplication and division are implemented to get the next number in the series.

9. Alternating Number Series: In this type of number series, several number patterns are used alternatively to form a series.

10. Wrong Number Series: In this type of number series, only one number doesn’t follow the same pattern as followed by the other numbers.

11. Fibonacci Number Series: In this type of number series, the next number is obtained by adding the two preceding or previous numbers.

How to Solve the Number Series Quickly?

The number series is an important and scoring topic in logical reasoning. Many questions have been seen in various exams. To solve the number series quickly the candidates must follow the following points:

1) The first step to approach the number series question is that the candidate must read the question thoroughly. Sometimes a thorough reading of a series of questions can be enough to reach a solution.

2) The second step is the candidate must check the pattern of the series it can be in increasing, decreasing or alternating order. After determining the pattern the candidate can find which mathematical operation is used in the series.

3) The third step is to find the correct missing number now if the series is in increasing order the candidate must apply the addition or multiplication operator, if the series is in decreasing order the candidate must apply the subtraction or division operator and if the series is alternatively increased or decreased the candidate must split the series into two parts and solve accordingly.

Tips and Number Series Reasoning Tricks

The useful tips and tricks for number series reasoning are as follows:

1) Determine the pattern of the series by analysing the series by determining the difference and by checking multiples etc between the consecutive terms. The candidates must check whether the series has one mathematical operation performed, two different operations are being alternately performed, or there is a mix of two series.

2) After determining the pattern the candidates must observe the difference between the given numbers in the series as it is either in increasing or decreasing order, and then the candidate must ensure that the questions belong to the addition or subtraction mathematical operator.

3) The candidates should try the next step if they are not able to spot an increasing or decreasing difference between the numbers. They should try to divide the second term with the first term, the second term with the third term of the series and so on. Now if the answer to the constant division comes as the same number, then the question belongs to the product series.

4) The candidates should learn the squares of all the natural numbers from 1 to 30 and learn the cubes of all the natural numbers from 1 to 25. Sometimes a series based on perfect squares or perfect cubes is given in a specific order and generally, one of the numbers is missing in this type of question candidates have to find this missing number and answer the question.

5) The candidate should not panic in case none of the above approaches works, the candidate must try writing every term of the question as to the multiplication of factor 2 and then try to identify a pattern between the given number in the series.

Solved Number Series Questions of Each Type

1) Increasing/ Addition Number Series
Example: Find the next number in the series: 2, 4, 8, 14, 22, ?

1) 28

2) 30

3) 32

4) 36

Solution:

The series follows the pattern of adding consecutive even numbers:

2 + 2 = 4; 4 + 4 = 8; 8 + 6 = 14; 14 + 8 = 22; 22 + 10 = 32

So, the next number in the series is 32. Hence, the third option is correct.

2) Decreasing/ Subtraction number series
Example: Which of the following numbers will replace the question mark (?) in the given series?
730, 692, 654, ?, 578

1) 612

2) 626

3) 616

4) 622

Solution

Let's check the difference between each number of the given series –

Like, 730 – 692 = 38

And, 692 – 654 = 38

Thus, the common difference between the two numbers is 38.

Similarly, 654 – 38 = 616

616 – 38 = 578

Thus, the missing number is 616. Hence, the third option is correct.

3) Multiplication number series
Example: Select the number from among the given options that can replace the question mark (?) in the following series.

242, 288, ?, 392, 450

1) 338

2) 375

3) 316

4) 324

Solution

Multiply the square of the consecutive natural numbers (starting from 11) by 2 to get the terms given in the series.

(11 × 11) × 2 = 121 × 2 = 242

(12 × 12) × 2 = 144 × 2 = 288

(13 × 13) × 2 = 169 × 2 = 338

(14 × 14) × 2 = 196 × 2 = 392

(15 × 15) × 2 = 225 × 2 = 450

So, 338 is the missing term in the series. Hence, the first option is correct.

4) Division Number Series
Example: Find the next number in the series: 1000, 200, 40, ?

1) 2

2) 10

3) 8

4) 20

Solution:

The series follows the pattern of dividing by 5

1000 ÷ 5 = 200; 200 ÷ 5 = 40; 40 ÷ 5 = 8

So, the next number will be 8. Hence, the third option is correct.

5) Square Number Series
Example: Which number will replace the question mark (?) to complete the given series?

148, 269, 413, ?, 778

1) 548

2) 512

3) 582

4) 614

Solution

Add the square of consecutive natural numbers starting from 11, to get the required missing term –

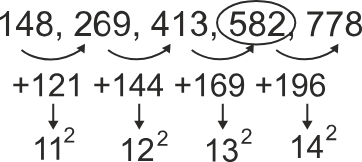
So, 582 is the required missing term in the series. Hence, the third option is correct.

6) Cube Number Series
Example: In the following question, select the missing number from the given series.
729, 512, 343, 216, ?

1) 36

2) 64

3) 25

4) 125

Solution

Find the cube roots of the given numbers to obtain the missing number of the series.

The numbers given in the series are the cubes of the natural numbers in descending order.
729 ⇒ ∛729 = 9
512 ⇒ ∛512 = 8
343 ⇒ ∛343 = 7
216 ⇒ ∛216 = 6
So, the next term of the series is 5³ = 125 Hence, the fourth option is correct.

7) Ascending/ Descending Number Series
Example: Which of the following numbers will replace the question mark (?) in the given series?
89, 170, 219, 244, 253, ?

1) 254

2) 257

3) 255

4) 256

Solution

Add the square of consecutive odd numbers in descending order starting from 9, to get the required missing number –
89 + 9² = 89 + 81 = 170;
170 + 7² = 170 + 49 = 219;
219 + 5² = 219 + 25 = 244;
244 + 3² = 244 + 9 = 253;
253 + 1² = 253 + 1 = 254

So, the missing number is 254. Hence, the first option is correct.

8) Mixed Number Series
Example: In the following question, select the missing number from the given series.
36, 18, 54, 27, 81, ?, 121.5

1) 40.5

2) 41.5

3) 40

4) 38

Solution
Divide and multiply the numbers by 2 and 3 alternatively.

The pattern is as follows –

36 ÷ 2 = 18; 18 × 3 = 54; 54 ÷ 2 = 27; 27 × 3 = 81; 81 ÷ 2 = 40.5; 40.5 × 3 = 121.5

So, the missing number of the series is 40.5. Hence, the first option is correct.

9) Alternating Number Series
Example: Select the number from among the given options that can replace the question mark (?) in the following series.

72, 85, 68, 81, ?, 77

1) 70

2) 61

3) 64

4) 67

Solution

Add 13 and subtract 17 alternatively from each term of the series to get the missing term of the series.

72 + 13 = 85; 85 – 17 = 68; 68 + 13 = 81; 81 – 17 = 64; 64 + 13 = 77

So, 64 is the missing number. Hence, the third option is correct.

10) Wrong Number Series
Example: Find the wrong number in the series.

225, 196, 169, 143, 121, 100

1) 143

2) 169

3) 121

4) 100

Solution

The number in the series are the squares of consecutive numbers in the decreasing order.

15² = 225; 14² = 196; 13² = 169; 12² = 144; 11² = 121; 10² = 100

Therefore, 143 is the wrong number in the series as square of 12 is 144. Hence, the first option is correct.

11) Fibonacci Number Series
Example: Find the next number in the series: 1, 1, 2, 3, 5, 8,?

1) 12

2) 13

3) 16

4) 10

Solution

The series follows the pattern of adding the two previous numbers to get the next number:

1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13

So, the missing number in the series is 13. Hence, the second option is correct.

Practice and Resources

The following are the recommended sources for the practice of the questions of the Venn diagram -
a) A Modern Approach to Verbal & Non-Verbal Reasoning by R.S. Aggarwal
b) Analytical Reasoning by M.K. Pandey
c) Logical and Analytical Reasoning by A.K. Gupta
d) Test of Reasoning by Edgar Thorpe
e) There are various number series pdfs, number series questions with solutions pdfs, number series for bank exam questions available online the candidate must practice online to excel the topic number series.

Question Weightage of Number Series in Competitive Exams

The number of questions based on the Number Series varies from exam to exam -
1) Questions asked in SSC exams i.e. SSC MTS, SSC CGL, SSC CHSL, SSC CPO, Steno - 1 to 2 questions.
2) Questions asked in the RRB exam i.e. Group D, NTPC, JE, ALP etc - 2 to 3 questions.
3) Questions asked in Banking exams, Bank PO, Bank Clerk - 3 to 4 questions.
4) Questions asked in various entrance exams such as CUET, TANCET, BITSAT, VITEEE, APICET, KMAT, and JIPMAT exams - 2 to 3 questions.

Number Series Reasoning Questions for Practice

1) Directions: Which of the following numbers will replace the question mark (?) in the given series?

8, ?, 20, 32, 48, 68

1) 14

2) 10

3) 12

4) 16

Hint: Add consecutive multiples of 4 to the numbers of the given series.

Solution

The pattern is as follows –

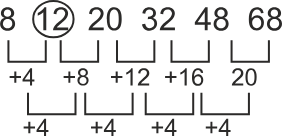
So, 12 is the missing number of the series. Hence, the third option is correct.

2) Directions: Which of the following numbers will replace the question mark (?) in the given series?

109, 113, 122, 147, ?

1) 196

2) 148

3) 154

4) 166

Hint: Check the difference between the number of the given series.

Solution

Add the square of consecutive prime numbers in each number, to get the required number –

109 + (2)2 = 109 + 4 = 113,

113 + (3)2 = 113 + 9 = 122,

122 + (5)2 = 122 + 25 = 147,

147 + (7)2 = 147 + 49 = 196

So, 196 is the missing number in the series. Hence, the first option is correct.

3) Directions: Which number will replace the question mark (?) in the following series?

57, 50, 55, 52, ?

1) 50

2) 53

3) 51

4) 55

Hint: Check the difference between the number of the given series.

Solution

Subtract and add the consecutive odd numbers alternatively (starting from 7) in decreasing order from each term to get the required missing number –

57 – 7 = 50, 50 + 5 = 55, 55 – 3 = 52, 52 + 1 = 53

So, the required missing number in the series is 53. Hence, the second option is correct.

4) Directions: Select the number from among the given options that can replace the question mark (?) in the following series.

2, 4, 7, 11, 16, 22, ?

1) 31

2) 54

3) 29

4) 28

Hint: Add consecutive natural numbers starting from 2, to get the next number.

Solution
The pattern is as follows:

2 + 2 = 4; 4 + 3 = 7; 7 + 4 = 11; 11 + 5 = 16; 16 + 6 = 22; 22 + 7 = 29

So, the required missing number in the series is 29. Hence, the third option is correct.

5) Directions: Which of the following numbers will replace the question mark (?) in the given series?

132, 156, 182, ?, 240

1) 198

2) 210

3) 216

4) 206

Hint: Determine the difference between two consecutive numbers, to obtain the required missing numbers.

Solution
Add consecutive even numbers starting from 24 in each number, to get the required missing number –

132 + 24 = 156; 156 + 26 = 182; 182 + 28 = 210; 210 + 30 = 240

So, the required missing number is 210. Hence, the second option is correct.

6) Directions: Which of the following numbers will replace the question mark (?) in the given series?

3, 7, 5, 61, 363 ?

1) 3367

2) 3348

3) 3630

4) 3267

Hint: Multiply numbers by odd numbers and add and subtract the square of even numbers alternatively, to get the required missing number.

Solution
The pattern is as follows:

3 × 1 + 22 = 3 + 4 = 7;

7 × 3 – 42 = 21 – 16 = 5;

5 × 5 + 62 = 25 + 36 = 61;

61 × 7 – 82 = 427 – 64 = 363;

363 × 9 + 102 = 3267 + 100 = 3367

So, 3367 is the required missing number. Hence, the first option is correct.

7) Directions: Which of the following numbers will replace the question mark (?) in the given series?
420, 462, 506, ?, 600, 650, 702

1) 564

2) 552

3) 562

4) 554

Hint: Add consecutive even numbers to the previous numbers to get the next numbers of the series.

Solution

The pattern is as follows:

420 + 42 = 462, 462 + 44 = 506, 506 + 46 = 552, 552 + 48 = 600, 600 + 50 = 650, 650 + 52 = 702

So, 552 is the missing number of the series. Hence, the second option is correct.

8) Directions: Which of the following numbers will replace the question mark (?) in the given series?

144, 127, 110, ?, 76, 59

1) 95

2) 93

3) 89

4) 97

Hint: Subtract 17 from the previous number to get the next number of the series.

Solution

The pattern is as follows:
144 – 17 = 127, 127 – 17 = 110, 110 – 17 = 93, 93 – 17 = 76, 76 – 17 = 59

So, 93 is the missing number of the series. Hence, the second option is correct.

9) Directions: Study the given pattern carefully and select the number that can replace the question mark (?) in it.

First row – 4, 6, 13

Second row – 9, 8, 21

Third row – 5, 6, ?

(NOTE: Operations should be performed on the whole numbers, without breaking down the numbers into their constituent digits. Eg. 13 – operations on 13 such as adding /subtracting /multiplying etc. to 13 can be performed. Breaking down 13 into 1 and 3 and then performing mathematical operations on 1 and 3 is not allowed.)

1) 14

2) 13

3) 12

4) 16

Hint: Add the first and second numbers, divide the second number by 2, and then add both the resultants, to get the third number.

Solution
The pattern is as follows:

In the first row: 4, 6, 13→(4 + 6) + (6 ÷ 2) = 10 + 3 = 13

In the second row: 9, 8, 21→(9 + 8) + (8 ÷ 2) = 17 + 4 = 21

Similarly, follow the same pattern in the third row: 5, 6, ?→(5 + 6) + (6 ÷ 2) = 11 + 3 = 14

So, the missing number is 14. Hence, the first option is correct.

10) Directions: Which of the following numbers will replace the question mark (?) in the given series?

64, 67, 76,103, ?

1) 145

2) 194

3) 184

4) 154

Hint: Check the difference between the number of the given series.

Solution

Add the power of 3 to the previous term to obtain the next term.

64 + (3)1 = 64 + 3 = 67,

67 + (3)2 = 67 + 9 = 76,

76 + (3)3 = 76 + 27 = 103,

103 + (3)4 = 103 + 81 = 184

So, 184 is the missing number. Hence, the third option is correct.

Wrong Number Series Reasoning Questions for Practice

1) Directions: Identify the number that does NOT belong to the following series.

1.5, 2, 3, 6, 18, 108, 1964

1) 108

2) 6

3) 18

4) 1964

Hint: For the given series, multiply the consecutive terms of the series to get the next term in the series.

Solution

1.5 × 2 = 3; 2 × 3 = 6; 3 × 6 = 18; 6 × 18 = 108; 18 × 108 = 1944

But the number given in the series is 1964.

So, from the given series, 1964 is incorrect. Hence, the fourth option is correct.

2) Directions: Identify the number that does not belong to the following series.

414, 430, 462, 526, 664, 910

1) 462

2) 526

3) 910

4) 664

Hint: Every number is double the previous number on checking the number difference in the series.

Solution

414 + 16 = 430; 430 + 32 = 462; 432 + 64 = 526; 526 + 128 = 654(but the given number is 664); 654 + 256 = 910

From the given series, we see that 664 is incorrect. Hence, the fourth option is correct.

3) Directions: In the given series one number is incorrect. Identify the INCORRECT number from among the options given.

3, 5, 7, 6, 10, 14, 12, 24, 28, 24, 40, 56

1) 10

2) 24

3) 12

4) 28

Hint: Think about splitting the series into three parts and then doubling the preceding numbers to obtain the next number.

Solution

Split the series into three parts.

(I) 3, 6, 12, 24

(II) 5, 10, 24, 40

(III) 7, 14, 28, 56

In all the series above the following number is double of the preceding number.

⇒ 3 + 3 = 6; 6 + 6 = 12; 12 + 12 = 24

⇒ 5 + 5 = 10; 10 + 10 = 20; 20 + 20 = 40

⇒ 7 + 7 = 14; 14 + 14 = 28; 28 + 28 = 56

In series (II) it is written 24 instead of 20.

So, 24 in the second series is the wrong number. Hence, the second option is correct.

4) Directions: In the following number series, two numbers have been put within brackets. Select the most appropriate option for these numbers in relation to their inclusion in the series.

21, 24, 19, (29), 17, 28, (15), 30

1) The first bracketed number (from the left) is correct and the second bracketed number (from the left) is incorrect.

2) Both the bracketed numbers are correct.

3) The first bracketed number (from the left) is incorrect and the second bracketed number (from the left) is correct.

4) Both the bracketed numbers are incorrect.

Hint: Determine the difference in alternative terms.

Solution
The pattern is as follows –

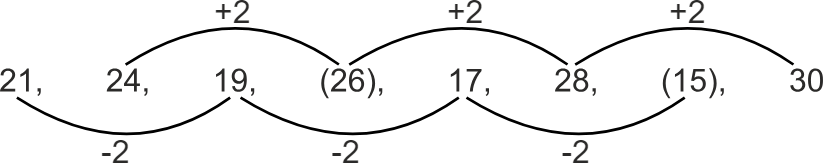
Therefore, the first bracketed number (from the left) is incorrect it should be 26 instead of 29 and the second bracketed number (from the left) is correct. Hence, the third option is correct.

5) Directions: Identify the number that does NOT belong to the following series.

30, 15, 15, 22.5, 46, 112.5

1) 46

2) 112.5

3) 22.5

4) 30

Hint: Multiply the numbers by consecutive numbers starting from 0.5

Solution

30 × 0.5 = 15

15 × 1 = 15

15 × 1.5 = 22.5

22.5 × 2 = 45

45 × 2.5 = 112.5

So, the wrong number in the series is 46. Hence, the first option is correct.

Read More: The list of verbal reasoning topics below.

Number Series Questions for Bank Exams

1) Directions: In the following number series, two numbers have been put within brackets. Select the most appropriate option for these numbers about their inclusion in the series.

1, 5, 17, (39), 65, 101, (145), 197

1) Both the bracketed numbers are correct

2) Both the bracketed numbers are incorrect

3) The first bracketed number from the left is correct and the second bracketed number from the left is incorrect

4) The first bracketed number from the left is incorrect and the second bracketed number from the left is correct

Hint: Determine the difference between two consecutive numbers to determine the correct number.

Solution

In the series given above the logic is defined by the figure given below:

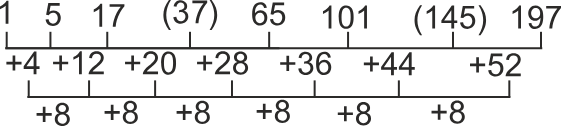
The number in the first bracket is replaced by 37 according to the given logic above.

So, the first bracket from the left is incorrect and the second bracket is correct. Hence, the fourth option is correct.

2) Directions: Select the number from among the given options that can replace the question mark (?) in the following series.

1, 3, 17, 55, ?, 179, 265, 375

1) 169

2) 157

3) 91

4) 105

Hint: Determine the difference between two consecutive numbers to obtain the required missing number.

Solution

The pattern is as follows –

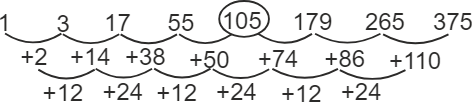
So, the required missing number in the series is 105. Hence, the fourth option is correct.

Number Series Questions for Competitive Exams and Entrance Exams

1) Directions: Select the number from among the given options that can replace the question mark (?) in the following series.

383, 381, 377, 369, 353, (?)

1) 325

2) 323

3) 322

4) 321

Hint: Determine the missing term by using difference and multiplication.

Solution
Follow the pattern to find the missing term –

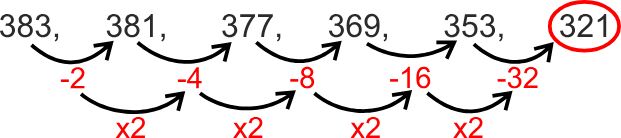
So, 321 is the missing term in the series. Hence, the fourth option is correct.

2) Directions: Which number will replace the question mark (?) to complete the given series?

55, 42, 31, 22, 15, 10,?

1) 7

2) 5

3) 3

4) 6

Hint: Check the difference between the numbers given in the series, to get the missing number.

Solution

Subtract the consecutive odd numbers in decreasing order (starting from 13), to get the missing number in the series.

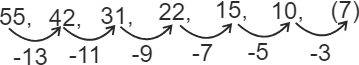
So, 7 is the missing term in the series. Hence, the first option is correct.

Number Series Questions for VITEEE Exam

1) Directions: Which number will replace the question mark (?) to complete the given series?

15, 16, 20, 29, 45, (?)

1) 70

2) 65

3) 75

4) 60

Hint: Determine the missing term by adding the squares of the consecutive natural numbers in the previous term.

Solution

Add the squares of the consecutive natural numbers in the previous term to get the next term.

15 + 12 = 15 + 1 = 16; 16 + 22 = 16 + 4 = 20; 20 + 32 = 20 + 9 = 29; 29 + 42 = 29 + 16 = 45; 45 + 52 = 45 + 25 = 70

So, 70 is the missing term in the series. Hence, the first option is correct.

2) Directions: Which of the following four options will replace the question mark (?) in the following series?

12, 36, ?, 102, 100, 300

1) 68

2) 34

3) 52

4) 76

Hint: Multiply by 3 and subtract 2 alternatively to get the missing number of the series.

Solution

12 × 3 = 36; 36 – 2 = 34; 34 × 3 = 102; 102 – 2 = 100; 100 × 3 = 300

So, 34 is the missing number. Hence, the second option is correct.

3) Directions: Select the number from among the given options that can replace the question mark (?) in the following series.

20, 110, 200, 290, 380, ?

1) 470

2) 490

3) 460

4) 480

Solution

Add 90 to each number to get the next number of the series –

20 + 90 = 110; 110 + 90 = 200; 200 + 90 = 290; 290 + 90 = 380; 380 + 90 = 470

So, the missing number is 470. Hence, the first option is correct.

4) Directions: In the following question, select the missing number from the given series.

1, 22, 44, 67, 91, ?

1) 116

2) 106

3) 115

4) 118

Hint: Check the difference between the numbers of the given series.

Solution

In the above-given series, add the increasing order of the numbers, starting from 21 to the previous number to get the next number of the series.

1 + 21 = 22; 22 + 22 = 44; 44 + 23 = 67; 67 + 24 = 91; 91 + 25 = 116

So, 116 is the missing number of the series. Hence, the first option is correct.

5) Directions: Which of the following numbers will replace the question mark (?) in the given series?

286, 192, 263, 176, 240, 160, 217, 144, ?

1) 186

2) 194

3) 165

4) 190

Hint: Determine the difference between two alternate numbers to obtain the required missing number.

Solution

Subtract 23 from numbers in odd positions and 16 from even position numbers –

So, 194 is the missing term in the series. Hence, the second option is correct.

For Non Verbal reasoning read the topics below:

About the Faculty
Tanu Gupta, with over a decade of experience as a reasoning faculty, specializes in preparing students for various entrance examinations and career development. Her extensive work with multiple educational platforms and institutions has honed her expertise in logical and analytical thinking. Her dedication to innovative teaching methods ensures these articles provide practical insights and expert guidance.