Series: Verbal Reasoning Practice Questions and Answers

Series reasoning is an important chapter in the logical reasoning which is asked in various government and entrance examinations like SSC, Bank, Railways, Defence, CUET, CAT, MAT, APICET, TANCET, KMAT, JIPMAT, VITEEE and others. In this article, we will be covering all the types of the series and also the approach to attempting such questions. As it is clear by the word ‘series’ itself any process which is running on a particular sequence. So, students need to find out these particular sequences in the given series in a question to get the answers.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: IBSAT 2024 Mock Tests | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

Question with Solutions: Missing Number | Alphabet Test | Arithmatical Problems | Calendar

This Story also Contains

1. Approach to Solve the Series Reasoning Questions
2. Types of Series Reasoning
3. Tips to Deal With the Series Reasoning Questions
4. Time Management Tips
5. Practice and Resources
6. Question Weightage of Series Reasoning Questions in Competitive Exams
7. Practice Questions For Repeating Pairs In Letter Series
8. Practice Questions For Find The Next Term In The Letter Series
9. Practice Questions For Missing Numbers In The Series
10. Practice Questions For Wrong Numbers In The Series
11. Practice Questions for the Mixed Series
12. Series Questions for CAT/ MAT/ APICET/ TANCET/ KMAT/ JIPMAT
13. Series Questions for APICET/ CUET
14. Series Questions for SSC/ RRB exams
15. Series Questions for Banking IBPS CWE Clerical/ IBPS RRB Clerical/ SBI Assistant/ Insurance Assistant exams

Approach to Solve the Series Reasoning Questions

To find the answers to the given series, aspirants need to determine the pattern being followed among the numbers, letters, words or symbols. They need to identify the common difference between the letters or numbers, or whether the given series of numbers are square, cubes or prime numbers.

Types of Series Reasoning

1. Letter-based Series

2. Number-based Series

3. Mixed Series

1. Letter-Based Series

In these types of series, the sequence of letters is given following a certain pattern. They are further classified into two types:

1. Repeating pair in letter series

2. Find the next term in the letter series
   
   1. Repeating pair in letter series

This type of series contains a sequence of letters arranged in a specific order with blanks at regular or irregular intervals. To solve, this type of series one should possess a strong understanding of the English alphabet and the pattern needs to be figured out to maintain the regularity of the sequence.

Let’s understand this type of series with the help of an example.

Example:
In the following question, a number of letters are given. There are blanks which can be filled with the help of the letters of the options below. Pick the correct option and complete the series:

_ aa _ ba _ bb _ ab _ aab
1) aaabb
2) babab
3) bbaab
4) bbbaa

Solution: To solve this question, first we need to divide the series into parts and then we need to fill in the blanks of each part with the letters given in the option one by one. Through this, we will be able to identify the pattern being followed in the given series easily.
The sequence given is _ aa _ ba _ bb _ ab _ aab.
First, divide the series:- _ aa _ / ba _ b / b _ ab / _ aab
Now, fill in the blanks with the given options one by one.
So, only third option makes a sequence as baab / baab / baab / baab.

2. Find the next term in the letter series

In this type of series, the letters are arranged in a specific sequence following a certain pattern. The elements of the series are referred to as ‘term’. To determine the pattern of the series, we need to know the place values of the letters of the alphabetical series.

The following are the different patterns of the letter series which we often see in exams:
1. Letters arranged in alphabetical order: This type of series consists of letters arranged in the order of the alphabetical series. For example, A, B, C, D, E.
2. Specific Patterns of letters at regular intervals: In this type of series, a specific pattern of letters is repeated at regular intervals. For example, AB, CD, EF, GH, IJ.
3. Letters being skipped at regular intervals: In this type of series, a certain number of letters is skipped between each consecutive letter. For example, A, C, E, G, H, I.
4. Arrangement of letters in Ascending or Descending Order: In this type of series, letters are arranged either in increasing or decreasing order based on their positions in the alphabetical series. For example, A, E, I, M, Q (ascending) or Z, V, R, N, J (descending).
5. Addition or subtraction of consecutive numbers to the place values of the letters: For example, A, C, F, J, O, U

Note: In logical reasoning to learn alphabet series reasoning tricks the candidates must practice several questions based on the alphabet series. Sequence and series reasoning questions are also provided in this article below for the reference of the candidates.

2. Number-Based Series

In number series reasoning a series consists of a sequence of numbers that follow a certain rule or formula. They can be classified into two groups -

a) Missing number in the series

b) Wrong number in the series

a) Missing Number In The Series

A series is given with a number or two missing in it. Aspirants need to identify a particular pattern which is taking the given series forward and then find out the missing number/numbers as per the pattern.

Example:
Which number will replace the question mark (?) in the following series?
58, 59, 51, 78, 14,?

a) 97 b) 139 c) 83 d) 163

Solution:

The pattern is as follows –
58 + (1)³ = 58 + 1 = 59
59 – (2)³ = 59 – 8 = 51
51 + (3)³ = 51 + 27 = 78
78 – (4)³ = 78 – 64 = 14
14 + (5)³ = 14 + 125 = 139
So, 139 is the missing number of the series. Hence, the second option is correct.

b) Wrong Number In Series

In this type of series, a number is incorrect. We need to find out the number by determining the pattern being followed in the series.
Example:
4, 10, 16, 21, 28, 34

a) 10 b) 21 c) 28 d) 34

Solution:

Here, the difference between the numbers of the series is 6. But the difference between 16 and 21 is 5. So, the wrong number is 21. Instead of 21, it should be 22. Hence, the second option is correct.

3. Mixed Series

This type of series consists of questions based on alphabet, numeric or both.

Example:

AK12, GV29, LF18, PO?

a) 32 b) 31 c) 38 d) 34

Answer:

The sum of the numeric position of the letters according to the English alphabet equals the number of the series. Place value of P = 16 and O = 15. So, the missing number = 16 + 15 = 31. Hence, the second option is correct.

Tips to Deal With the Series Reasoning Questions

To solve series-based questions, an aspirant must have basic knowledge of the following subjects -

1. English Language: Place values of the letters, opposite letters etc.

2. Mathematics: squares and square roots, cubes and cube roots, Prime numbers etc.

Time Management Tips

The concept of series is scoring and easy to understand for every aspirant. Thus, spending at most 2 to 3 minutes on the questions based on the series is suggested. Try to attempt letter and number-based series questions first in the examinations as these questions are based on alphabetical series and addition and subtraction.

The candidates who are preparing for the upcoming entrance and Government exams can also refer to the links given below and master the reasoning ability section:

Practice and Resources

1. A Modern Approach to Verbal & Non-Verbal Reasoning by RS Aggarwal

2. Perfect Verbal Reasoning By Ajay Chauhan

3. SSC Reasoning by Rakesh Yadav

4. Logical and Analytical Reasoning by AK Gupta

5. The candidate must practice questions online as many number series reasoning questions pdf, alphabet series reasoning questions pdf, letter series reasoning questions pdf and series reasoning questions pdf are available online.

Question Weightage of Series Reasoning Questions in Competitive Exams

The number of questions based on series varies from exam to exam -

1) Series questions asked in SSC exams i.e. SSC MTS, SSC CGL, SSC CHSL, SSC CPO, Steno - 2 to 4 questions.

2) Series questions asked in Banking exams i.e., IBPS PO, IBPS Clerk, RRB PO, RRB Clerk - 5 to 6 questions.

3) Series questions asked in the RRB exam i.e. Group D, NTPC, JE, ALP etc - 2 to 3 questions.

4) Series questions asked in CUET, KMAT, JIPMAT, APICET, CAT, NPAT and other college entrance exams - 1 to 2 questions.

Practice Questions For Repeating Pairs In Letter Series

1. Directions: Select the option that represents the letters that when sequentially placed from left to right in the blanks below will complete the letter series.

YO_LECT_OPL_C_YOP_ _CTYOPLE_T

1. PEYTELC

2. PYETLEC (correct)

3. PYECTLE

4. PEYTLCE

Solution-

Given:

YO_LECT_OPL_C_YOP__CTYOPLE_T

To fill the series we have to divide the series – YO_LECT / _OPL_C_ / YOP__CT / YOPLE_T

Let's check each option –

First option: PEYTELC; YOPLECT / EOPLYCT/ YOPELCT / YOPLECT (No repetitive pattern is followed)

Second option: PYETLEC; YOPLECT / YOPLECT / YOPLECT / YOPLECT (YOPLECT is repeated)

Third option: PYECTLE; YOPLECTYOPLECCYOPTLCTYOPLEET (No repetitive pattern is followed)

Fourth option: PEYTLCE; YOPLECTEOPLYCTYOPLCCTYOPLEET (No repetitive pattern is followed)

So, only the second option follows a pattern. Hence, the second option is correct.

2. Directions: Select the option that represents the letters that when placed from left to right in the following blanks will complete the letter series.

ASDF_A_ _FG_UD_GA_ _FG

1. GTDAFVD (correct)

2. FTEAFWD

3. FTDAFVD

4. GTEAGXE

Solution-

Given:

ASDF_A_ _FG_UD_GA_ _FG

To fill the series we have to divide the series – ASDF_ / A_ _FG / _UD_G / A_ _FG

Let's check each option –

First option: GTDAFVD; ASDFG / ATDFG / AUDFG / AVDFG (In each part, the second letter is increased by 1 place, and the rest of the letters are the same)

Second option: FTEAFWD; ASDFF / ATEFG / AUDFG / AWDFG (No repetitive pattern is followed)

Third option: FTDAFVD; ASDFF / ATDFG / AUDFG / AVDFG (No repetitive pattern is followed)

Fourth option: GTEAGXE; ASDFG / ATEFG / AUDGG / AXEFG (No repetitive pattern is followed)

So, only the first option follows a pattern. Hence, the first option is correct.

3. Directions: Select the option that represents the letters that when sequentially placed from left to right in the blanks below will complete the letter series.

T_OJEW_TRO_EWF_ROJ_WFTR_JE_F

1. RFJTEOW (correct)

2. RJFOTWE

3. RJFTWOE

4. RFJOTEW

Solution-

Given:

T_OJEW_TRO_EWF_ROJ_WFTR_JE_F

To fill the series we have to divide the series – T_OJEW_ / TRO_EWF / _ROJ_WF / TR_JE_F

Let's check each option –

First option: RFJTEOW; TROJEWF / TROJEWF / TROJEWF / TROJEWF (TROJEWF is repeated)

Second option: RJFOTWE; TROJEWJ / TROFEWF / OROJTWF / TRWJEEF (No repetitive pattern is followed)

Third option: RJFTWOE; TROJEWJ / TROFEWF / TROJWWF / TROJEEF (No repetitive pattern is followed)

Fourth option: RFJOTEW; TROJEWF / TROJEWF / OROJTWF / TREJEWF (No repetitive pattern is followed)

So, only the first option follows a pattern. Hence, the first option is correct.

4. Directions: Select the option that represents the letters that, when placed from left to right in the blanks below, will complete the letter series.

_RQ_PR_S_ _QSPRQ_

1. PQRSPR

2. PSQPRS (correct)

3. PSRQPS

4. PRQSPS

Solution-

Given:

_RQ_PR_S_ _QSPRQ_

Check the order of the letters in the given series.

To fill the series we have to divide the series – _RQ_ / PR_S / _ _QS / PRQ_

Let's check the options –

First option: PQRSPR; PRQQ/ PRRS / SPQS / PRQR (No repeated pattern has been found.)

Second option: PSQPRS; PRQS / PRQS / PRQS / PRQS (PRQS is the repeated letter cluster.)

Third option: PSRQPS; PRQS / PRRS / QPQS / PRQS (No repeated pattern has been found.)

Fourth option: PRQSPS; PRQR / PRQS / SPQS / PRQS (No repeated pattern has been found.)

So, PRQS is the repeated letter cluster in the second option. Hence, the second option is correct.

5. Directions: In the following question, which set of letters, when sequentially placed in the gaps in the given letter series, will complete it?

c_e_cd_f_d_f

1. dfcec

2. dfece (correct)

3. cfede

4. cdfed

Solution-

Given:

c_e_cd_f_d_f

Divide the series into letter clusters – c_ e_ / cd _f /_d _f

Let's check each option –

First option: dfcec; cdef / cdcf / edcf (No repeated pattern found.)

Second option: dfece; cdef / cdef / cdef (cdef is repeated in the series.)

Third option: cfede; ccef / cdef / ddef (No repeated pattern found.)

Fourth option: cdfed; cced / cdff / eddf (No repeated pattern found.)

So, the series becomes→cdefcdefcdef. Hence, the second option is correct.

Practice Questions For Find The Next Term In The Letter Series

1. Directions: Select the letter cluster from among the given options that can replace the question mark (?) in the following series.

PQJ, LMF, HIB, DEX, ?

1. ZAV

2. ZBT

3. ZAT (correct)

4. ZAU

Solution-

Given:

PQJ, LMF, HIB, DEX, ?

Subtract 4 from each letter of the given term, to get the required missing term.

PQJ→P – 4 = L; Q – 4 = M; J – 4 = J→LMF

LMF→L – 4 = H; M – 4 = I; F – 4 = B→HIB

HIB→H – 4 = D; I – 4 = E; B – 4 = X→DEX

DEX→D – 4 = Z; E – 4 = A; X – 4 = T→ZAT

Therefore, the required missing term in the series is ZAT. Hence, the third option is correct.

2. Directions: Which of the following letter clusters will replace the question mark (?) in the given series?

ZBQ, BFL, ?, FNB, HRW, JVR

1. DKG

2. DJF

3. DJG (correct)

4. DKF

Solution-

Given:

ZBQ, BFL, ?, FNB, HRW, JVR

Add 2 and 4 to the place values of the first and second letters and subtract 5 from the place value of the third letter of the given clusters to get the letters of the next term.

ZBQ→Z + 2 = B; B + 4 = F; Q – 5 = L→BFL

BFL→B + 2 = D; F + 4 = J; L – 5 = G→DJG

DJG→D + 2 = F; J + 4 = N; G – 5 = B→FNB

FNB→F + 2 = H; N + 4 = R; B – 5 = W→HRW

HRW→H + 2 = J; R + 4 = V; W – 5 = R→JVR

So, DJG is the required letter cluster of the series. Hence, the third option is correct.

3. Directions: Which of the following terms will replace the question mark (?) in the given series?

XGR, TKN, POJ, LSF, ?, DAX

1. HVB

2. HWB (correct)

3. GWB

4. HWA

Solution-

Given:

XGR, TKN, POJ, LSF, ?, DAX

Subtract and add 4 alternatively to the place values of the letters in the clusters.

XGR→X – 4 = T; G + 4 = K; R – 4 = N→TKN

TKN→T – 4 = P; K + 4 = O; N – 4 = J→POJ

POJ→P – 4 = L; O + 4 = S; J – 4 = F→LSF

LSF→L – 4 = H; S + 4 = W; F – 4 = B→HWB

HWB→H – 4 = D; W + 4 = A; B – 4 = X→DAX

So, HWB is the required missing term of the series. Hence, the second option is correct.

4. Directions: Which letter cluster will replace the question mark (?) to complete the given series?

BZVR, DXWQ, ?, HTYO, JRZN

1. FXPV

2. FXPN

3. FVXP (correct)

4. FVPX

Solution-

Given:

BZVR, DXWQ, ?, HTYO, JRZN

Add 2, and 1 to the first and the third letters respectively, and subtract 2 and 1 from the second and the fourth letters of the previous term to get the next term in the series.

BZVR→B + 2 = D; Z – 2 = X; V + 1 = W; R – 1 = Q→DXWQ

DXWQ→D + 2 = F; X – 2 = V; W + 1 = X; Q – 1 = P→FVXP

FVXP→F + 2 = H; V – 2 = T; X + 1 = Y; P – 1 = O→HTYO

HTYO→H + 2 = J; T – 2 = R; Y + 1 = Z; O – 1 = N→JRZN

So, FVXP is the missing term of the series. Hence, the third option is correct.

5. Directions: Which of the following letter clusters will replace the question mark (?) in the given series to make it logically complete?

ADZ, GJF, MPL, SVR, ?

1. XYB

2. YBX (correct)

3. XBY

4. YXB

Solution-

Given:

ADZ, GJF, MPL, SVR, ?

Add 6 to each letter cluster to get the next term in the given series –

ADZ→A + 6 = G, D + 6 = J, Z + 6 = F→GJF

GJF→G + 6 = M, J + 6 = P, F + 6 = L→MPL

MPL→M + 6 = S, P + 6 = V, L + 6 = R→SVR

SVR→S + 6 = Y, V + 6 = B, R + 6 = X→YBX

So, YBX is the missing term. Hence, the second option is correct.

Practice Questions For Missing Numbers In The Series

1. Directions: Which of the following numbers will replace the question mark (?) in the given series?

1, 4, 27, 16, 125, ?

1. 216

2. 36 (correct)

3. 343

4. 49

Solution-

Given:

1, 4, 27, 16, 125, ?

In the above-given series –

(1)³ = 1; (2)² = 4; (3)³ = 27; (4)² = 16; (5)³ = 125

According to the above pattern, the next number will be – (6)² = 36

So, 36 is the missing term. Hence, the second option is correct.

2. Directions: Which of the following numbers will replace the question mark (?) in the given series?

18, 20, 22, 27, 32, 39, ?

1. 47

2. 42

3. 46 (correct)

4. 45

Solution-

Given:

18, 20, 22, 27, 32, 39,?

Add 2, 5, and 7 to the numbers in the series to get the next term respectively.

18 + 2 = 20; 20 + 2 = 22; 22 + 5 = 27; 27 + 5 = 32; 32 + 7 = 39; 39 + 7 = 46

So, 46 is the missing number of the series. Hence, the third option is correct.

3. Directions: Select the number from among the given options that can replace the question mark (?) in the following series.

31, 37, 46, 60, 81, ?

1. 117

2. 106

3. 122

4. 111 (correct)

Solution-

Given:

31, 37, 46, 60, 81, ?

The difference of the numbers being added to the terms of the series is an odd number.

The pattern is as follows –

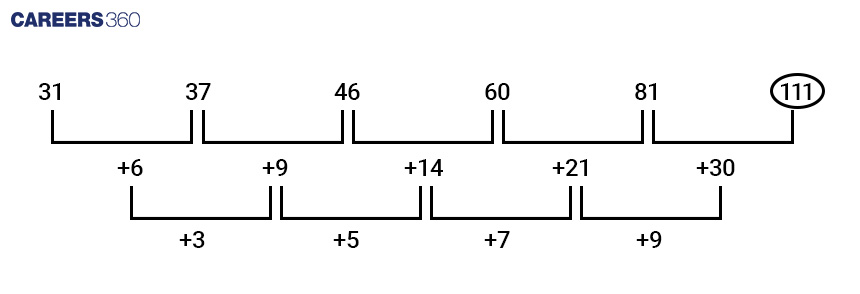
So, 111 is the missing number of the given series. Hence, the fourth option is correct.

4. Directions: Which of the following numbers will replace the question mark (?) in the given series?

27, 38, ?, 68, 87, 110

1. 47

2. 50

3. 51 (correct)

4. 53

Solution-

Given:

27, 38, ?, 68, 87, 110

Add consecutive prime numbers (starting from 11) to each number in the given series to get the next number of the series.

27 + 11 = 38; 38 + 13 = 51; 51 + 17 = 68; 68 + 19 = 87; 87 + 23 = 110

So, 51 is the missing number. Hence, the third option is correct.

5. Directions: Which of the following numbers will replace the question mark (?) in the given series?

3, 8, 15, 26, 39, ?

1. 61

2. 49

3. 52

4. 56 (correct)

Solution-

Given:

3, 8, 15, 26, 39, ?

Add consecutive prime numbers (starting from 5) to each number in the given series to get the next number of the series.

3 + 5 = 8; 8 + 7 = 15; 15 + 11 = 26; 26 + 13 = 39; 39 + 17 = 56

So, 56 is the missing term. Hence, the fourth option is correct.

Practice Questions For Wrong Numbers In The Series

1. Directions: Identify the number that does NOT belong to the following series.

104, 108, 54, 58, 29, 31

1. 58

2. 29

3. 54

4. 31 (correct)

Solution-

Given:

104, 108, 54, 58, 29, 31

Add 4 and divide the number by 2 alternatively in each number, to determine the wrong number in the series –

104 + 4 = 108; 108 ÷ 2 = 54; 54 + 4 = 58; 58 ÷ 2 = 29; 29 + 4 = 33 ≠ 31

So, 31 does not belong to the series. Hence, the fourth option is correct.

2. Directions: Select the number from among the given options that can replace the question mark (?) in the following series.

1, 3, 17, 55, ?, 179, 265, 375

1. 169

2. 157

3. 91

4. 105 (correct)

Solution-

Given:

1, 3, 17, 55, ?, 179, 265, 375

The pattern is as follows –

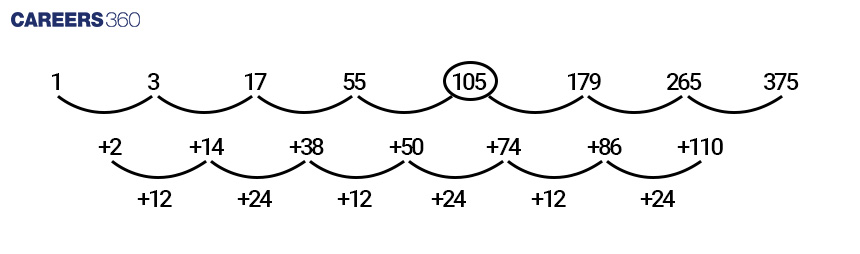
So, the required missing number in the series is 105. Hence, the fourth option is correct.

3. Directions: Identify the number that does NOT belong to the following series.

30, 15, 15, 22.5, 46, 112.5

1. 46 (correct)

2. 112.5

3. 22.5

4. 30

Solution-

Given:

30, 15, 15, 22.5, 46, 112.5

Multiply the numbers by 0.5; 1; 1.5; 2; and 2.5 to obtain the next number.

30 × 0.5 = 15

15 × 1 = 15

15 × 1.5 = 22.5

22.5 × 2 = 45

45 × 2.5 = 112.5

So, the wrong number in the series is 46. Hence, the first option is correct.

4. Directions: Identify the number that does not belong to the following series.

414, 430, 462, 526, 664, 910

1. 462

2. 526

3. 910

4. 664 (correct)

Solution-

Given:

414, 430, 462, 526, 664, 910

414 + 16 = 430; 430 + 32 = 462; 432 + 64 = 526; 526 + 128 = 654(but the given number is 664); 654 + 256 = 910

From the given series, we see that 664 is incorrect. Hence, the fourth option is correct.

5. Directions: Identify the number that does NOT belong to the following series.

1.5, 2, 3, 6, 18, 108, 1964

1. 108

2. 6

3. 18

4. 1964 (correct)

Solution-

Given:

1.5, 2, 3, 6, 18, 108, 1964

Multiply consecutive terms of the series to get the next term –

1.5 × 2 = 3; 2 × 3 = 6; 3 × 6 = 18; 6 × 18 = 108; 18 × 108 = 1944

But the number given in the series is 1964.

So, from the given series, 1964 is incorrect. Hence, the fourth option is correct.

Practice Questions for the Mixed Series

1. Directions: The following series has one term missing. Select the correct alternative from the options below to complete the series.

A7F, E15J, I23N, ?

1. R13M

2. M31R (correct)

3. R23M

4. R37S

Solution-

Given:

A7F, E15J, I23N, ?

Add 4 to each letter and 8 to each number of the previous term to obtain the next term in the series.

A7F→A + 4 = E; 7 + 8 = 15; F + 4 = J→E15J

E15J→E + 4 = I; 15 + 8 = 23; J + 4 = N→I23N

I23N→I + 4 = M; 23 + 8 = 31; N + 4 = R→M31R

M31R is the missing term of the series. Hence, the second option is correct.

2. Directions: A series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.

?, Planning, Strategy, Marketing, Finance

1. Realization

2. Success

3. Failure

4. Idea (correct)

Solution-

Given:

?, Planning, Strategy, Marketing, Finance

To start a business, we need to come up with an idea, plan accordingly, strategize to implement the idea, identify target markets, and consider the finances required throughout the entire process.

So, the order of steps of the startup business project is as follows –

Idea < Planning < Strategy < Marketing < Finance

So, the idea is the missing term of the given series. Hence, the fourth option is correct.

3. Directions: A series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.

Jaipur, Rajasthan, India, ?

1. Europe

2. Antarctica

3. Asia (correct)

4. Australia

Solution -

Given:

Jaipur, Rajasthan, India, ?

To complete the series, we need to provide a larger geographical region that encompasses India.

Asia has a larger geographical region that encompasses India.

So, the order of the series is like –

Jaipur < Rajasthan < India < Asia

So, Asia is the missing term of the given series. Hence, the third option is correct.

4. Directions: In the following question, a series is given with one or more term(s) missing. Choose the correct alternative from the given options.

az225, cx423, ev621, _?, _?

1. jq1116, kp1215

2. go1314, mn126

3. gt819, ir1017 (correct)

4. gu720, gt819

Solution-

Given:

az225, cx423, ev621, _?, _ ?

az225→a + 2 = c; a and z are opposite pairs; 225 + 198 = 423

cx423→c + 2 = e; c and x are opposite pairs; 423 + 198 = 621

ev621→e + 2 = g; e and v are opposite pairs; 621 + 198 = 819

gt819→g + 2 = i; g and t are opposite pairs; 819 + 198 = 1017

So, gt819 and ir1017 are the missing terms of the series. Hence, the third option is correct.

5. Directions: In the following question, a series is given with one (or more) number(s)/alphabet missing. Choose the correct alternative from the given options.

J2Z, K4X, L7V, M11T, ?

1. O17R

2. N17S

3. R16N

4. N16R (correct)

Solution-

Given:

J2Z, K4X, L7V, M11T, ?

Add 1 to the place value of the first letter and add consecutive natural numbers starting from 2 to the number of the previous term respectively, and subtract 2 from the third letter to obtain the next term in the series –

J2Z→J + 1 = K; 2 + 2 = 4; Z – 2 = X→K4X

K4X→K + 1 = L; 4 + 3 = 7; X – 2 = V→L7V

L7V→L + 1 = M; 7 + 4 = 11; V – 2 = T→M11T

M11T→M + 1 = N; 11 + 5 = 16; T – 2 = R→N16R

So, N16R is the missing term of the series. Hence, the fourth option is correct.

Series Questions for CAT/ MAT/ APICET/ TANCET/ KMAT/ JIPMAT

1) Directions: A series is given with one term missing. Select the correct alternative from the given ones that will complete the series.

ABC, WHP, SNC, OTP, ?

1) KQR

2) KAC

3) KZC

4) KYB

Hint: Subtract 4 from the place value of the first letter and, add 6 and 13 to the place value of the second and third letters of the previous term, to obtain the next term in the series.

Solution:

ABC→A – 4 = W; B + 6 = H; C + 13 = P→WHP

WHP→W – 4 = S; H + 6 = N; P + 13 = C→SNC

SNC→S – 4 = O; N + 6 = T; C + 13 = P→OTP

OTP→O – 4 = K; T + 6 = Z; P + 13 = C→KZC

So, KZC is the missing term in the series. Hence, the third option is correct.

2) Directions: Which one set of letters when sequentially placed in the gaps in the given letter series shall complete it?

no_m _l _o _m _ln_r _al

1) naromra

2) ranraom

3) noamrna

4) manrmao

Hint: Divide the series into parts and fill in the blanks with the options one by one to identify the pattern of the given series.

Solution:

To fill the series, we have to divide the series – no_m _l / _o _m _l / n_r _al

Let's check the options –

First option: naromra; nonmal / roomml / nrraal (No repeated pattern found.)

Second option: ranraom; normal / normal / normal (normal is repeated in the series.)

Third option: noamrna; nonmol / aommrl / nnraal (No repeated pattern found.)

Fourth option: manrmao; nommal / normml / naroal (No repeated pattern found.)

So, the series becomes→normalnormalnormal. Hence, the second option is correct.

3) Directions: Which of the following numbers will replace the question mark (?) in the given series?

730, 692, 654, ?, 578

1) 612

2) 626

3) 616

4) 622

Hint: Find the difference between the numbers to obtain the missing number of the series.

Solution:

Let's check the difference between each number of the given series –

Like, 730 – 692 = 38

And, 692 – 654 = 38

Thus, the common difference between the two numbers is 38.

Similarly, 654 – 38 = 616

616 – 38 = 578

Thus, the missing number is 616.

Hence, the third option is correct.

Series Questions for APICET/ CUET

1) Directions: A series is given with one term missing. Select the correct alternative from the given ones that will complete the series.

RTM, VZX, ZFI, DLT, ?

1) HRE

2) RST

3) TMO

4) HRS

Hint: Add 4, 6, and 11 to the place value of the first, second, and third letters of the previous term to get the next term.

Solution:

RTM→R + 4 = V; T + 6 = Z; M + 11 = X

VZX→V + 4 = Z; Z + 6 = F; X + 11 = I

ZFI→Z + 4 = D; F + 6 = L; I + 11 = T

DLT→D + 4 = H; L + 6 = R; T + 11 = E

So, HRE is the missing term of the given series. Hence, the first option is correct.

2) Directions: Which of the following numbers will replace the question mark (?) in the given series?

29, 33, ?, 113, 369

1) 55

2) 51

3) 54

4) 49

Hint: Add 4, 16, 64, and 256 to the numbers of the given series.

Solution:

The pattern is as follows –

29 + (2)2 = 29 + 4 = 33

33 + (2 × 2)2 = 33 + (4)2 = 33 + 16 = 49

49 + (2 × 4)2 = 49 + (8)2 = 49 + 64 = 113

113 + (2 × 8)2 = 113 + (16)2 = 113 + 256 = 369

So, 49 is the missing number. Hence, the fourth option is correct.

3) Directions: Which letter cluster will replace the question mark (?) to complete the given series?

NAME, NEME, ?, NOME, NUME

1) NMME

2) NKME

3) NIME

4) NJME

Hint: N, M, and E are constant in each term and each second letter of the given terms is a vowel.

Solution:

NAME, NEME, ?, NOME, NUME

N, M, and E are constant in each term and each second letter of the given terms is a vowel (a, e, i, o, u). Put these vowels in second place to obtain the next term in the series.

NAME→A is a vowel and next is E.

NEME→E is a vowel and next is I.

NIME→I is a vowel and next is O.

NOME→O is a vowel and next is U.

So, NIME is the missing term in the series. Hence, the third option is correct.

Series Questions for SSC/ RRB exams

1) Directions: Select the combination of letters that when sequentially placed in the blanks of the given series will make the series logically complete.

F_HIEH_JDIF_ _JEL

1) ELFX

2) GGKC

3) KGGG

4) FGEL

Hint: Substitute each option to find out the repeating pattern.

Solution:

To fill the series we have to divide the series – F_HI / EH_J / DIF_ / _JEL

Let's check each option –

First option: ELFX; FEHI / EHLJ / DIFF / XJEL (No repeated pattern has been found)

Second option: GGKC; FGHI / EHGJ / DIFK / CJEL (The first letter decreased by 1, the second letter increased by 1, the third letter decreased by 1 and the fourth letter increased by 1 in the given series)

Third option: KGGG; FKHI / EHGJ / DIFG / GJEL (No repeated pattern has been found)

Fourth option: FGEL; FFHI / EHGJ / DIFE / LJEL (No repeated pattern has been found)

So, the series becomes→FGHIEHGJDIFKCJEL. Hence, the second option is correct.

3) Directions: Which of the following letter clusters will replace the question mark (?) in the given series to make it logically complete?

CMW, MWG, WGQ, GQA, ?

1) AKQ

2) KAQ

3) QAK

4) QBL

Hint: Add 10 to the place value of each letter of the previous term to obtain the next term in the series.

Solution:

Here, add 10 to the place value of each letter of the previous term to obtain the next term in the series –

CMW→C + 10 = M; M + 10 = W; W + 10 = G

MWG→M + 10 = W; W + 10 = G; G + 10 = Q

WGQ→W + 10 = G; G + 10 = Q; Q + 10 = A

GQA→G + 10 = Q; Q + 10 = A; A + 10 = K

So, QAK is the missing term in the series. Hence, the third option is correct.

3) Directions: What should come in place of the question mark (?) in the given series?

84, 89, 98, 111, 128, ?

1) 139

2) 132

3) 149

4) 143

Hint: Determine the difference between two consecutive terms to get the required missing term.

Solution:

The difference between given numbers in the series is increasing by 4.

84 + 5 = 89; 89 + 9 = 98; 98 + 13 = 111; 111 + 17 = 128; 128 + 21 = 149

So, 149 is the missing term in the series. Hence, the third option is correct.

Series Questions for Banking IBPS CWE Clerical/ IBPS RRB Clerical/ SBI Assistant/ Insurance Assistant exams

1) Directions: What should come in place of the question mark (?) in the given series?

42, 30, ?, 12, 6, 2

1) 24

2) 20

3) 18

4) 22

Hint: Subtract even numbers in decreasing order starting from 12 from the previous number to get the next number of the series.

Solution:

In the above-given series, subtract even numbers in decreasing order starting from 12 from the previous number to get the next number.

42 – 12 = 30; 30 – 10 = 20; 20 – 8 = 12; 12 – 6 = 6; 6 – 4 = 2

So, the missing number is 20. Hence, the second option is correct.

2) Directions: Select the term from the given options that can replace the question mark (?) in the given series to make it logically complete.

BP 74, ?, FT 64, HV 59, JX 54

1) CS 70

2) DR 69

3) ET 68

4) ES 70

Hint: Add 2 to the place value of the letters and subtract 5 from the number to get the next term of the series.

Solution:

Add 2 to both the letters and subtract 5 from the number to get the next term of the series –

BP 74→B + 2 = D; P + 2 = R; 74 – 5 = 69→DR 69

DR 69→D + 2 = F; R + 2 = T; 69 – 5 = 64→FT 64

FT 64→F + 2 = H; T + 2 = V; 64 – 5 = 59→HV 59

HV 59→H + 2 = J; V + 2 = X; 59 – 5 = 54→JX 54

So, the missing term is DR 69. Hence, the second option is correct.

3) Directions: What should come in place of the question mark (?) in the given series?

48, 100, ?, 1232, 6170

1) 306

2) 280

3) 304

4) 214

Hint: Multiply the numbers with consecutive natural numbers from 2 onwards and add consecutive even numbers from 4 onwards to find the next term.

Solution:

In the given series, multiply the numbers with consecutive natural numbers from 2 onwards and add consecutive even numbers from 4 onwards to find the next term.

(48 × 2) + 4 = 96 + 4 = 100;

(100 × 3) + 6 = 300 + 6 = 306;

(306 × 4) + 8 = 1224 + 8 = 1232;

(1232 × 5) + 10 = 6160 + 10 = 6170

So, the missing number is 306. Hence, the first option is correct.

For non verbal reasoning read the topics below:

About the Faculty
Tanu Gupta, with over a decade of experience as a reasoning faculty, specializes in preparing students for various entrance examinations and career development. Her extensive work with multiple educational platforms and institutions has honed her expertise in logical and analytical thinking. Her dedication to innovative teaching methods ensures these articles provide practical insights and expert guidance.