Venn Diagram: Meaning, Reasoning Questions and Answers, Formula, Examples

The Venn diagram is an important topic mostly seen in the reasoning section and the questions from this topic are usually asked in various competitive exams and entrance exams such as Banking, SSC, RRB, Insurance, CUET etc. This topic is considered one of the easiest topics in the reasoning.
What is Venn diagram? A Venn diagram is a diagram that uses circles and represents the relationship between a given group of words. It is a method that helps to determine all the possible relationships between a given group of words with a single diagram. When circles intersect, they share similar features, but when circles do not overlap, they don't have those features in common.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: IBSAT 2024 Mock Tests | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

Question with Solutions: Missing Number | Alphabet Test | Arithmatical Problems | Calendar

This Story also Contains

1. Venn Diagram Reasoning: Types of Venn Diagrams
2. Practice and Resources
3. Question Weightage of Venn Diagram in Competitive Exams
4. Venn Diagram Reasoning Practice Questions For Venn Diagram to Relation
5. Venn Diagram Reasoning Practice Questions For Relation to Venn Diagram
6. Venn Diagram Reasoning Practice Questions For Caselets
7. Venn Diagram Reasoning Practice Questions For the Representation-based Venn Diagram
8. Venn Diagram Reasoning Questions for AP ICET/ IBSAT
9. Venn Diagram Reasoning Questions for KMAT/ UPESMET/ JIPMAT
10. Venn Diagram Reasoning Questions for SSC CHSL/ SSC Stenographer/ SSC CGL/ SSC CPO exams
11. Venn Diagram Reasoning Questions for IBPS CWE Clerical/ IBPS RRB Assistant/ Railway Recruitment Board exams

Venn Diagram Reasoning: Types of Venn Diagrams

There are several types of questions that have been seen from the Venn diagram reasoning in exams -

1. Venn diagram to a relation

2. Relation to the Venn diagram

3. Caselets

4. Representation-based Venn diagram

Let’s discuss these types in detail with the help of examples -

1. Venn Diagram to Relation

In this type of Venn diagram, a Venn diagram will be given and we have to determine the most suitable group of words that matches the relationship with the given Venn diagram. Let’s understand the concept with the help of Venn diagram examples with solutions.

Example: Select the set of classes and the relationship among which is best illustrated by the Venn diagram given below.

A) Shoes, Watches, Goggles

B) Spectacles, Pens, Diaries

C) Reptiles, Snakes, Lizards

D) Daughter, Son, Brother

Answer: To identify the words associated with the given Venn diagram, let's analyse the diagram. The diagram consists of two small circles within a larger circle, indicating that the two circles belong to the same category represented by the larger circle. Since the two small circles do not intersect or overlap, they do not share any similarities. Now, if we check the options, it is clear that only the third option satisfies the condition stated by the given Venn diagram. In this case, both snakes and lizards fall under the category of reptiles and are not interconnected.

2. Relation to Venn Diagram

In this type of Venn diagram, a group of words will be given and we have to find the most suitable Venn diagram that represents the possible relationship between the given words. Let’s understand the concept with the help of Venn diagram examples with solutions.

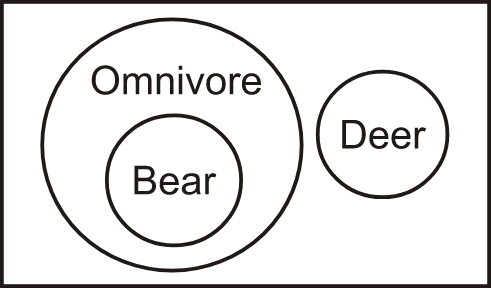
Example: Determine the Venn diagram that represents the relationship between Omnivores, Bear, and Deer.

Answer: As we know, Deer only eats grass. This means that deer is a herbivore and not an omnivore. But, a Bear is both a carnivore and herbivore, i.e., a Bear is an omnivore. So, all bears are omnivores while no deer is omnivore. Deer and bears are not related to each other. So, the circle representing the bear will lie inside the circle representing the omnivore, and the circle representing the deer will be drawn separately.

So, the Venn diagram is –

3. Caselets

Data Caselet questions are mostly seen in the reasoning section of the CAT exam. This topic is very important from the CAT exam and bank exams point of view. In these types of questions, candidates are given a caselet and a set of questions are asked based on the given caselet. A data caselet is basically a paragraph that contains certain data or information. No charts or graphs are provided with the data. We have to organise the data from the caselet and then solve the related set of questions. Some questions can be solved by using the table and some questions can be solved directly just by interpreting the data. Some of the questions are solved using the Venn diagrams. The questions are easily solvable as only basic mathematical concepts are used to answer most of the questions.

Example: In a batch of 60 students, 50% of the students scored more than 80% and 70% scored more than 50% in a test. There were 10% of the students who scored less than 15 on that test. How many students scored between 15 and 60 marks if the total marks were 75?

Solution: Total marks = 75

80% of 75 = (80/100) × 75 = 60

Students who scored more than 60 = 50% of 60 = 30 —---- (I)

Students who scored less than or equal to 60 = 30 —---- (II)

Students who scored less than 15 = 10% of 60 = 6 —---- (III)

Now, on subtracting equation (III) from equation (II), we will get the students who score between 15 and 60.

So, students who scored between 15 and 60 = 30 - 6 = 24

4. Representation-based Venn Diagram

In this type of Venn diagram, a Venn diagram will be given with different geometrical shapes indicating different categories with one or more than one number in each figure. In this, we have to identify how many persons belong to different categories according to the given conditions. Let’s understand the concept with the help of Venn diagram examples with solutions.

Example: In the given figure, how many people like cricket and tennis?

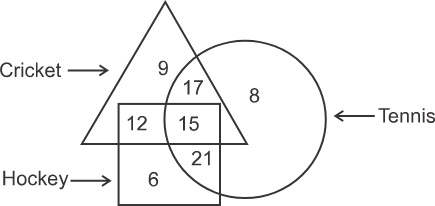
Answer: To get the number of people who like cricket and tennis, determine the sum of the numbers falling in the part of the diagram where the regions representing Cricket, Hockey and Tennis overlap. In the below diagram, the shaded part represents the region common to both cricket and tennis as well as hockey. The numbers of the asked fields that fall in the hockey region will also be counted as there is no direction given that the region belonging to hockey can not be included.

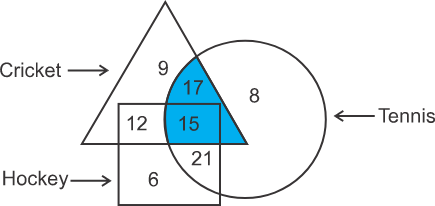
The total number of people who like cricket and tennis both = 17 + 15 = 32

Therefore, 32 people like both cricket and tennis. Hence, the second option is correct.

Practice and Resources

The following are the recommended sources for the practice of the questions of the Venn diagram -
a) A Modern Approach to Verbal & Non-Verbal Reasoning by R.S. Aggarwal

b) Analytical Reasoning by M.K. Pandey

c) Logical and Analytical Reasoning by A.K. Gupta

d) Test of Reasoning by Edgar Thorpe

Question Weightage of Venn Diagram in Competitive Exams

The number of questions based on the Venn diagram varies from exam to exam -
1) Questions asked in SSC exams i.e. SSC MTS, SSC CGL, SSC CHSL, SSC CPO, Steno - 2 to 3 questions.
2) Questions asked in the RRB exam i.e. Group D, NTPC, JE, ALP etc - 2 to 3 questions.
3) Questions asked in Banking exams, Bank PO, Bank Clerk - 1 to 2 questions.

For practice Venn diagram questions, understanding Venn diagram meaning, Venn diagram symbols, Venn diagram reasoning tricks, Venn diagram formula, candidates must download the logical Venn diagram reasoning questions with solutions pdf below:
Venn Diagram Questions with Solutions PDF

Venn Diagram Reasoning Practice Questions For Venn Diagram to Relation

Q1. Directions: Select the set of classes and the relationship among which is best illustrated by the Venn diagram given below.

A) Fruits, Mango, Apple (Correct)

B) Eatables, Vegetables, Potato

C) Pen, Eraser, Sharpener

D) Brother, Husband, Man

Solution: To identify the words associated with the given Venn diagram, let's analyse the diagram. The diagram consists of two small circles within a larger circle, indicating that the two circles belong to the same category represented by the larger circle. Since the two small circles do not intersect or overlap, they do not share any similarities. Now, if we check the options, it is clear that only the first option satisfies the condition stated by the given Venn diagram. In this case, both mango and apple fall under the category of fruits and are not interconnected.

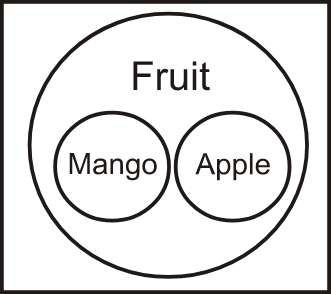
Hence, the first option is correct.

Q2. Directions: Select the set of classes and the relationship among which is best illustrated by the Venn diagram given below.

A) Husband, Father, Man

B) Man, Woman, Human

C) Brother, Man Woman (Correct)

D) Vegetable, Fruit, Eatables

Solution: To identify the words associated with the given Venn diagram, let's analyse the diagram. The diagram consists of one small circle within a larger circle, indicating that the smaller circle belongs to the category represented by the larger circle. Also, there is one separate circle from the two circles, indicating that this circle belong to a different category. Now, if we check the options, it is clear that only the third option satisfies the condition stated by the given Venn diagram. In this case, the brother falls under the category of man. But the woman is a different category.

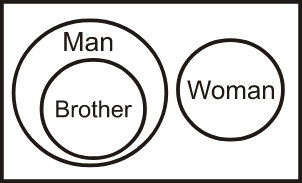
Hence, the third option is correct.

Q3. Directions: Select the set of classes and the relationship among which is best illustrated by the Venn diagram given below.

A) Parents, Mothers, Fathers

B) Females, Sisters, Teachers

C) Women, Wives, Sisters (Correct)

D) Humans, Women, Men

Solution: To identify the words associated with the given Venn diagram, let's analyse the diagram. The diagram consists of one small circle within a larger circle, indicating that the smaller circle belongs to the category represented by the larger circle. Also, one more circle overlaps two circles, indicating that this circle shares some common properties. Now, if we check the options, it is clear that only the second option satisfies the condition stated by the given Venn diagram. In this case, it is quite evident that all the sisters belong to the category of females. Those who are teachers can either be male or female and some of them can also be sisters. So, the circle representing teachers will overlap with the circles representing sisters and females.

Hence, the third option is correct.

Q4. Directions: Select the set of classes and the relationship among which is best illustrated by the Venn diagram given below.

A) Colours, Red, Green

B) Notebook, Stationery, Uniform

C) Pen, Pencil, Stationery

D) Pen, Pencil, Eraser (Correct)

Solution: To identify the words associated with the given Venn diagram, let's analyse the diagram. The diagram consists of three non-overlapping circles, indicating that all three circles are different from each other and do not share any common features. Now, if we check the options, it is clear that only the fourth option satisfies the condition stated by the given Venn diagram. In this case, it is quite evident that Pen, Pencil and Eraser are stationery items but are not interconnected.

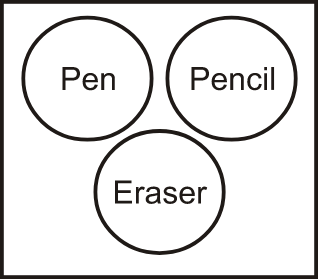
Hence, the fourth option is correct.

Q5. Directions: Select the set of classes and the relationship among which is best illustrated by the Venn diagram given below.

A) Sportsmen, Cricketers, Batsman

B) Material, Cement, Wood

C) Police, Thief, Criminal (Correct)

D) Teacher, Dramatist, Painter

Solution: To identify the words associated with the given Venn diagram, let's analyse the diagram. The diagram consists of one small circle within a larger circle, indicating that the smaller circle belongs to the category represented by the larger circle. Also, there is one separate circle from the two circles, indicating that this circle belong to a different category. Now, if we check the options, it is clear that only the third option satisfies the condition stated by the given Venn diagram. In this case, the thief falls under the category of criminal. But the police belong to a different category.

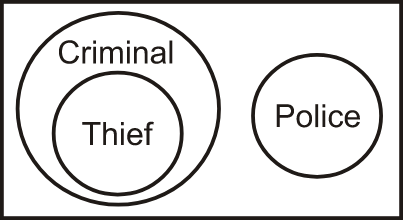
Hence, the third option is correct.

Venn Diagram Reasoning Practice Questions For Relation to Venn Diagram

Q1. Directions: Which of the following diagrams represents the relationship among Sweets, Ladoo, and Jalebi?

A) B) C) (Correct) D)

Solution: Both Ladoo and Jalebi are Sweets. So, all Ladoo are sweets and all Jalebi are sweets. So, the circles representing Ladoo and Jalebi will lie inside the circle representing Sweets. But, Jalebi and Ladoo are not related to each other. So, their circles will not intersect with each other.

The Venn diagram will be –

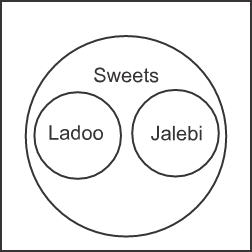
Hence, the third option is correct.

Q2. Directions: Which of the following diagrams represents the relationship among the given classes?

Earth, Crust, Mantle, Core

A) B) C) (Correct) D)

Solution: Earth is the name given to the entire planet. Its outermost layer is called the crust, while the layer beneath the crust is known as the mantle. The core is located at the centre of the Earth. Although the crust, mantle, and core are all parts of Earth, they are not directly related to each other. So, all three circles representing the crust, the mantle, and the core will lie inside the circle representing Earth.

So, the Venn diagram is –

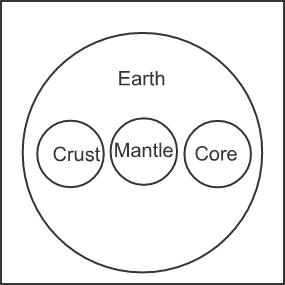
Hence, the third option is correct.

Q3. Directions: Which of the following diagrams represents the relationship between Pen, Ink, and Refill?

A) B) (Correct) C) D)

Solution: We know that ink is present inside a refill. So, the circle that represents ink will lie inside the circle that represents refill. Also, a refill is present inside a pen. So, the circle representing refill will lie inside the circle representing the pen.

The Venn diagram will be –

Hence, the second option is correct.

Q4. Directions: Which of the following diagrams represents the relationship between Kidney, Foot, and Head?

A) B) (Correct) C) D)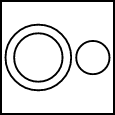

Solution: The kidney, foot, and head are all different parts of the human body. They are not related to each other in any manner. So, their circles will be drawn separately.

So, the correct Venn diagram is –

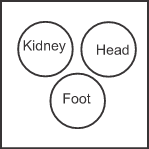
Hence, the second option is correct.

Q5. Directions: In the following question, identify the diagram that represents the best relationship among the classes given below.

Children, Serious, Naughty

A) (Correct) B) C) D)

Solution: Children can either be serious or naughty. So, the circle of children will have an overlapping with the circles of serious and naughty. But no one can be serious and naughty at the same time. So, both the circles will not have any direct relationship with each other.

Therefore, the Venn diagram is as follows –

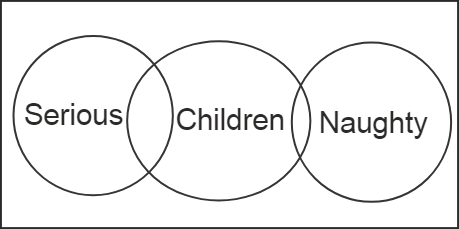
Hence, the first option is correct.

Venn Diagram Reasoning Practice Questions For Caselets

Q1. Directions: At a certain school, each of the 150 students takes at least 1 of the three 3 classes. The 3 classes available are English, Hindi, and Spanish. 60 students study English, 85 study Hindi, and 52 study Spanish. If 5 students take all 3 classes, then how many take exactly 2 classes?

A) 22

B) 25

C) 31

D) 37 (Correct)

Solution: Based on the above-given data, let’s consider the following Venn diagram:

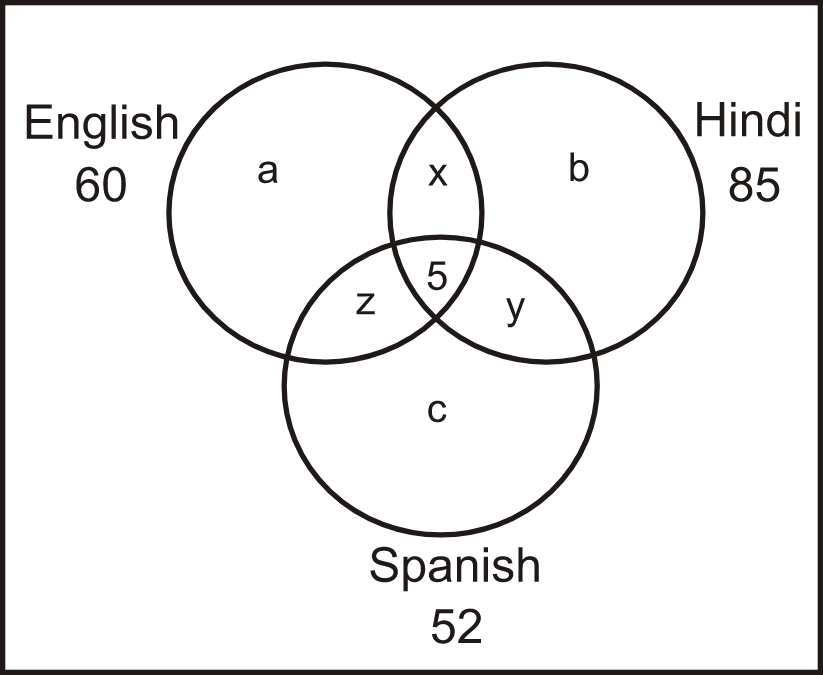
According to the diagram,

a + b + c + x + y + z + 5 = 150

a + b + c + x + y + z = 145 —------(I)

Also, a + b + c + 2(x + y + z) + 3(5) = 60 + 85 + 52

a + b + c + 2(x + y + z) + 15 = 197

a + b + c + 2(x + y + z) = 182 —------(II)

To get the number of students who take exactly 2 classes, subtract equation (I) from the (II).

(x + y + z) = 182 - 145 = 37

So, 37 students took exactly 2 subjects. Hence, the fourth option is correct.

Q2. In a locality, there are a total of 500 families. Each family reads at least 1 newspaper. It is known that 250 families read ‘The Hindu’, 180 families read ‘Times of India’, and 200 families read ‘Indian Express’. If it is known that exactly 50 families read all three newspapers then how many families read exactly 2 newspapers?

A) 22

B) 30 (Correct)

C) 35

D) 27

Solution: Based on the above-given data, let’s consider the following Venn diagram:

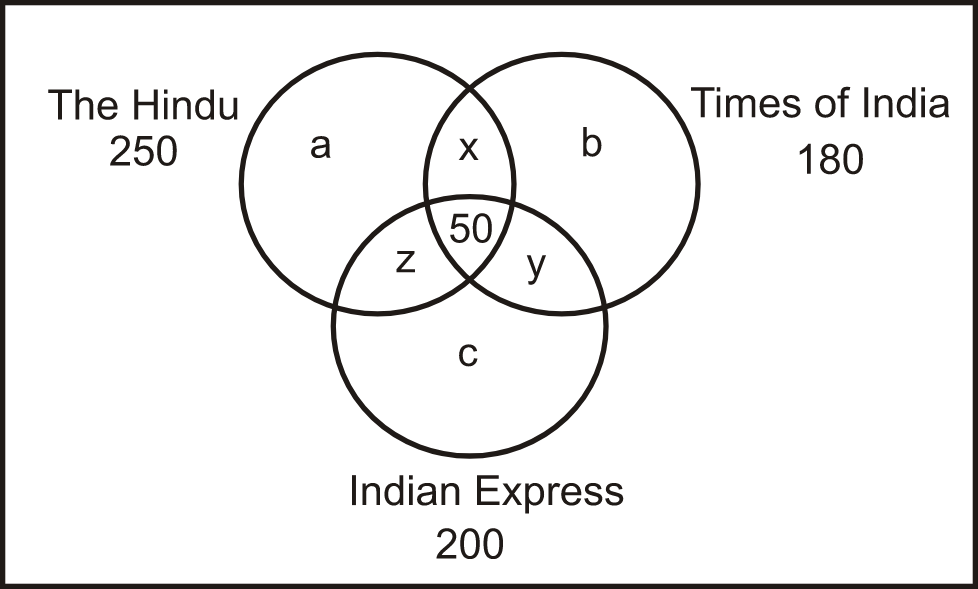
According to the diagram,

a + b + c + x + y + z + 50 = 500

a + b + c + x + y + z = 450 —------(I)

Also, a + b + c + 2(x + y + z) + 3(50) = 250 + 180 + 200

a + b + c + 2(x + y + z) + 150 = 630

a + b + c + 2(x + y + z) = 480 —------(II)

To get the number of students who take exactly 2 classes, subtract equation (I) from the (II).

(x + y + z) = 480 - 450 = 30

So, 30 families read exactly 2 newspapers. Hence, the second option is correct.

Q3. Directions: There are 450 students in a college. Each student has to choose one or more electives out of economics, geography, and math. Further, the following information is also known:

1. 80 students selected only economics and math.

2. 91 students selected only economics and geography.

3. 60 students selected only math and geography.

4. The number of students who selected only geography is 145 less the number of students who selected only economics.

5. In total 250 students selected economics as an elective.

6. In total 255 students selected geography as an elective.

How many students selected both math and economics as electives?

A) 85

B) 91

C) 95

D) 99 (Correct)

Solution: Let ‘x’ be the number of students who took all the three electives and ‘y’ be the number of students who took only economics as an elective. Based on the given information, the Venn diagram is as follows:

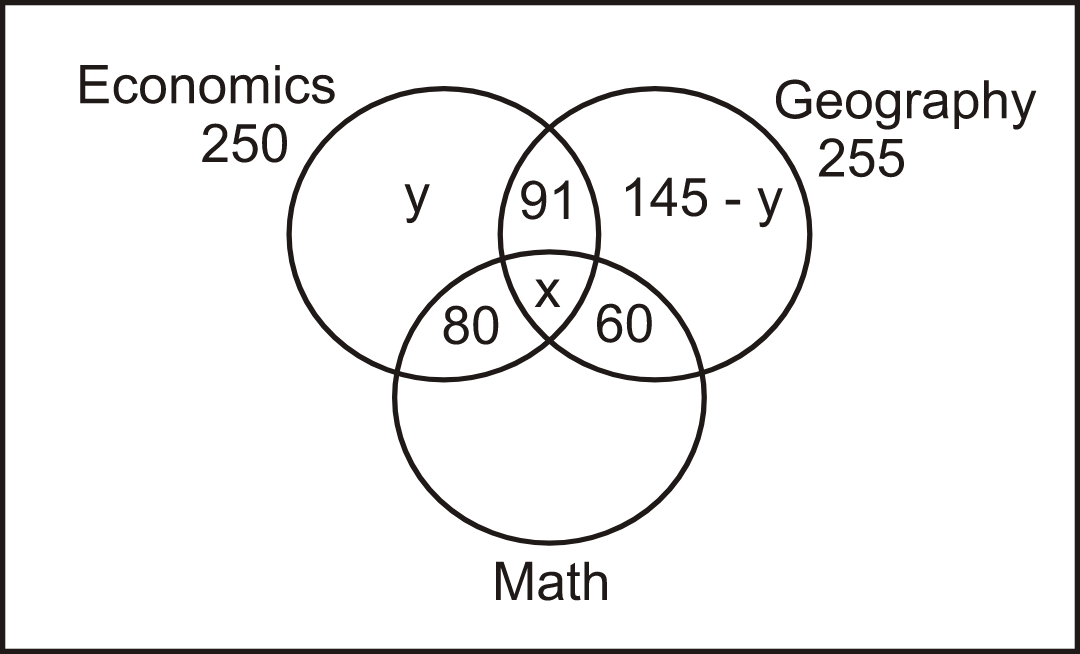
Let’s consider the students who took economics as an elective, we have,

91 + 80 + x + y = 250 ⇒ x + y = 79 —-------(I)

Let’s consider the students who took geography as an elective, we have,

91 + x + 60 + 145 - y = 255 ⇒ y - x = 41 —-------(II)

Adding both the equations, we get, 2y = 120 ⇒ y = 60

So, x = 19

So, number of students who took all the three as electives = 19

Number of students who took only economics as an elective = 60

Number of students who took only geography as an elective = 85

Number of students who took only math as an elective = 450 - 255 - 60 - 80 = 55

Thus, we got the following Venn diagram:

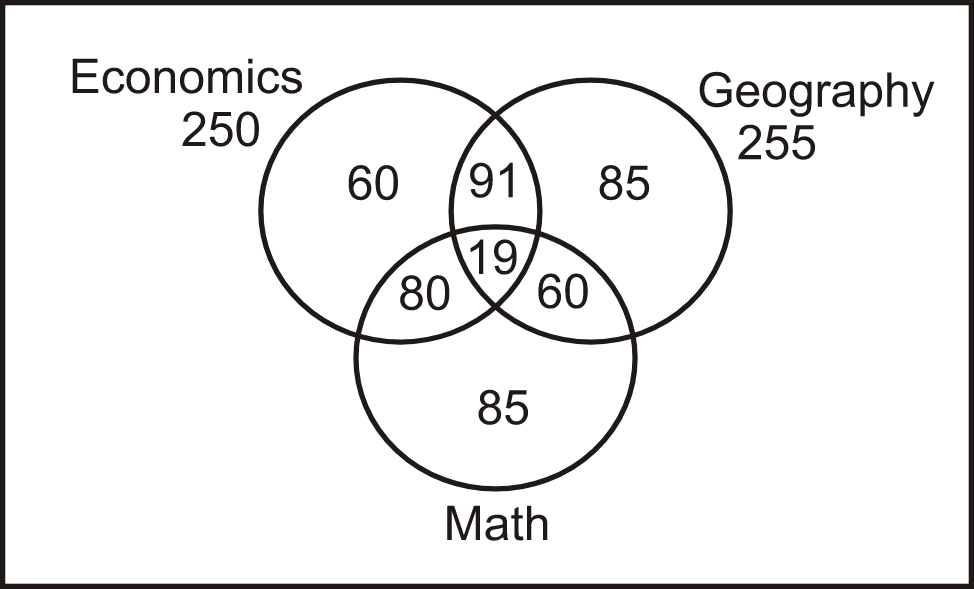
Number of students who selected both economics and math as electives = 80 + 19 = 99

Hence, the fourth option is correct.

Q4. Directions: There are 450 students in a college. Each student has to choose one or more electives out of economics, geography, and math. Further, the following information is also known:

1. 80 students selected only economics and math.

2. 91 students selected only economics and geography.

3. 60 students selected only math and geography.

4. The number of students who selected only geography is 145 less the number of students who selected only economics.

5. In total 250 students selected economics as an elective.

6. In total 255 students selected geography as an elective.

How many students selected only economics as an elective?

A) 80

B) 60 (Correct)

C) 55

D) 19

Solution: Let ‘x’ be the number of students who took all the three electives and ‘y’ be the number of students who took only economics as an elective. Based on the given information, the Venn diagram is as follows:

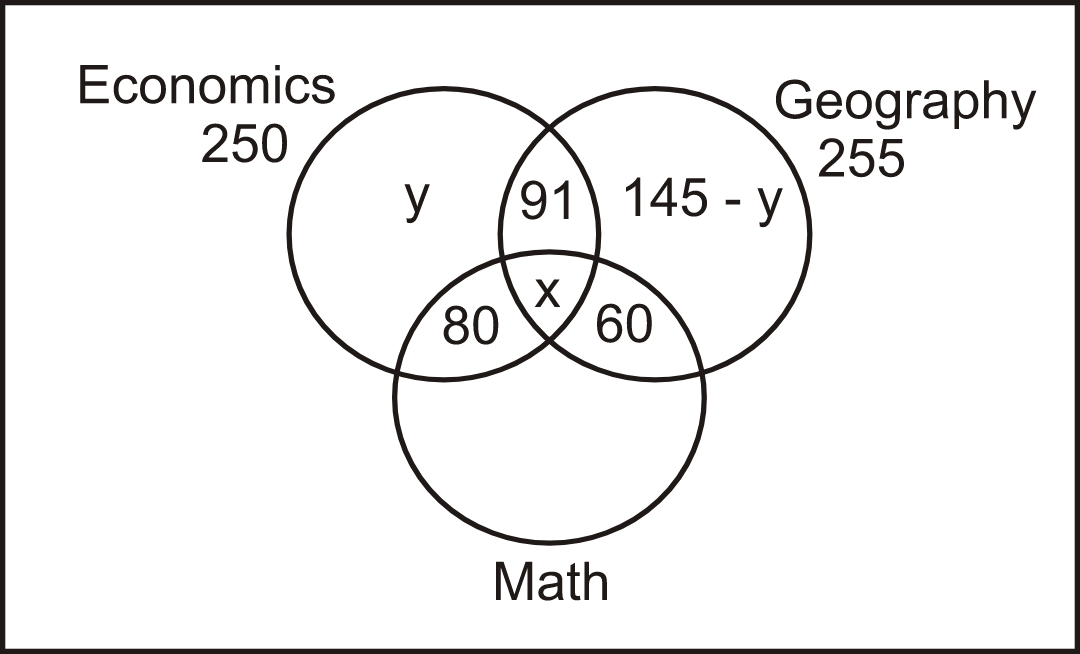
Let’s consider the students who took economics as an elective, we have,

91 + 80 + x + y = 250 ⇒ x + y = 79 —-------(I)

Let’s consider the students who took geography as an elective, we have,

91 + x + 60 + 145 - y = 255 ⇒ y - x = 41 —-------(II)

Adding both the equations, we get, 2y = 120 ⇒ y = 60

So, x = 19

So, number of students who took all the three as electives = 19

Number of students who took only economics as an elective = 60

Number of students who took only geography as an elective = 85

Number of students who took only math as an elective = 450 - 255 - 60 - 80 = 55

Thus, we got the following Venn diagram:

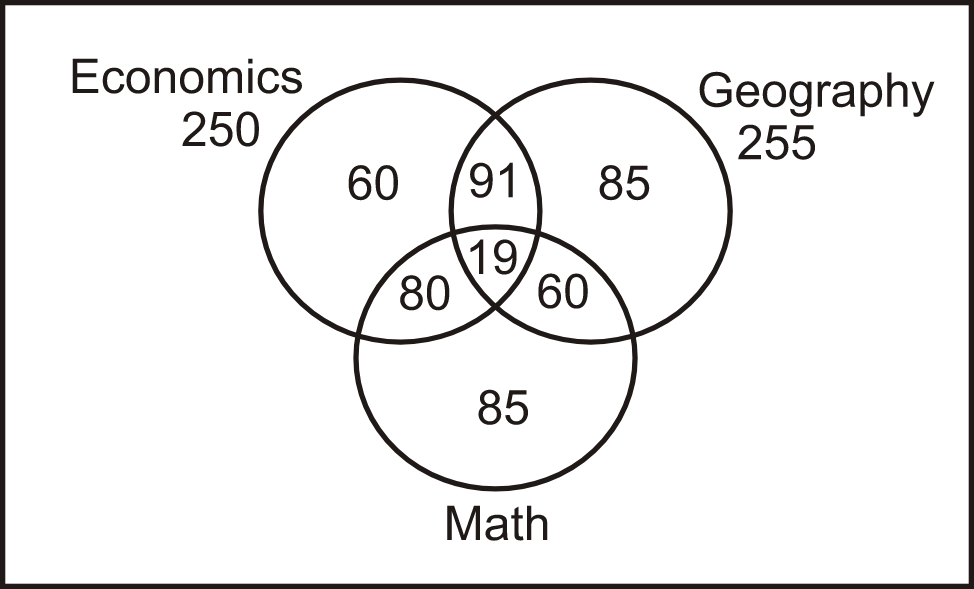
Number of students who selected only economics as an elective = 60

Hence, the second option is correct.

Q5. Directions: 500 people are living in a particular village. There are three drinks Tea, Coffee, and Hot chocolate available in the village. Each citizen has to vote for one or more of the three drinks which he/she likes. It is known that:

1. In total 180 people like Tea and 220 people like Coffee.

2. 60 people like all the three drinks.

3. 80 people like both Tea and Hot chocolate.

4. 79 people like both Hot chocolate and Coffee.

5. 91 people like both Tea and Coffee.

How many people like only Tea?

A) 69 (Correct)

B) 59

C) 60

D) 70

Solution: According to the given information, 46 people like all three drinks. For the given data, the Venn diagram is as follows:

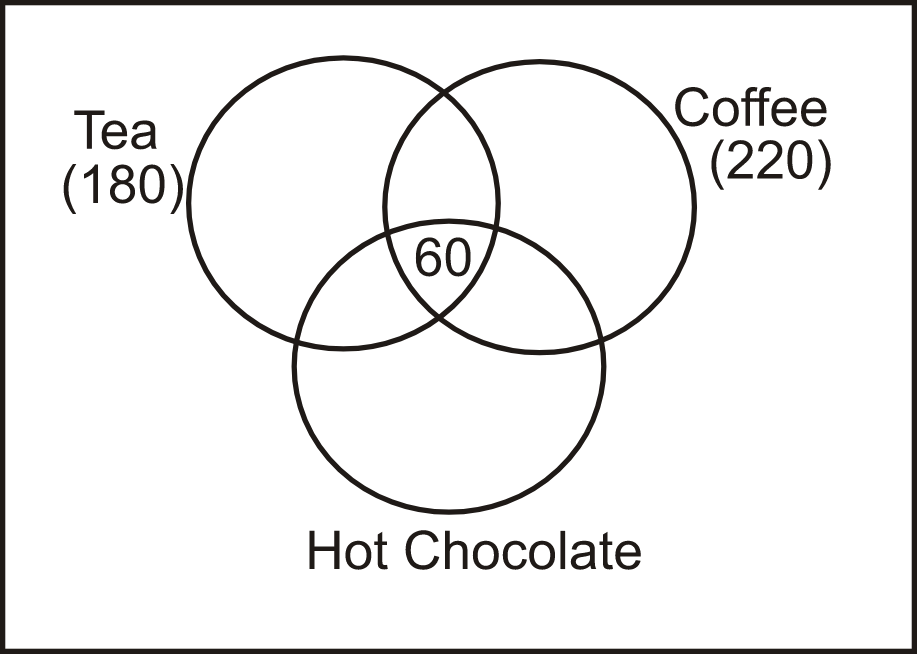
Since, 80 people like both Tea and Hot chocolate. So, the number of people who like only Tea and Hot chocolate = 80 - 60 = 20

Since, 79 people like both Hot chocolate and Coffee. So, the number of people who like only Hot chocolate and Coffee = 79 - 60 = 19

Since, 91 people like both Tea and Coffee. So, the number of people who like only Tea and Coffee = 91 - 60 = 31

Thus, we got the following Venn diagram:

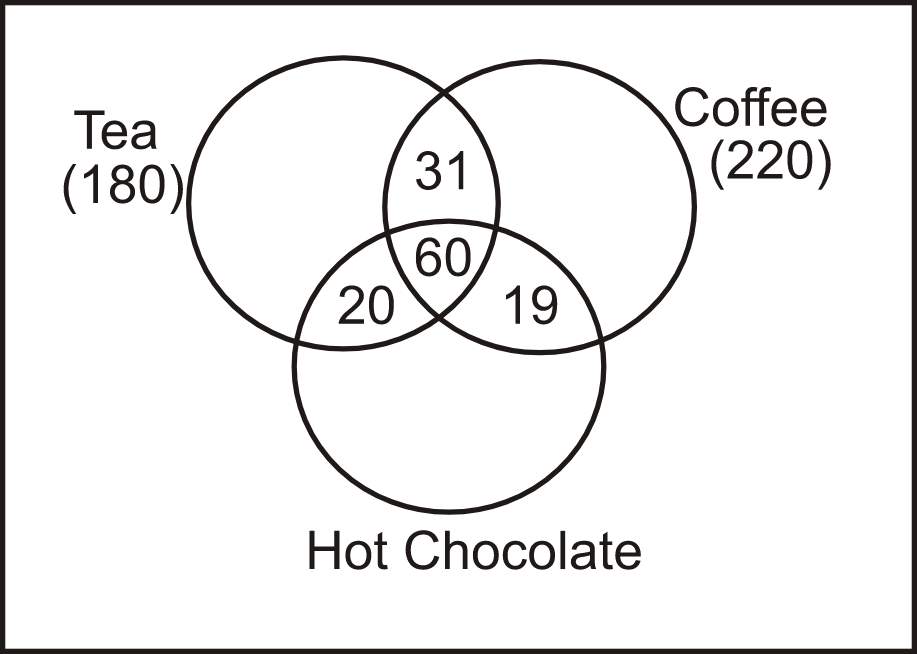
So, the number of people who like only Tea = 180 - 20 - 60 - 31 = 69

Hence, the first option is correct.

Venn Diagram Reasoning Practice Questions For the Representation-based Venn Diagram

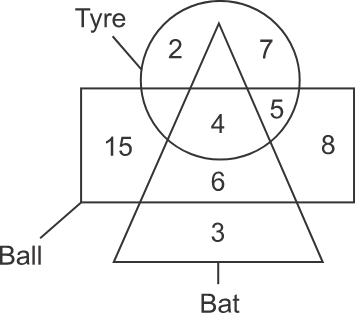
Q1. Directions: How many balls are neither the bat nor the tyre?

A) 15

B) 21

C) 23 (Correct)

D) 8

Solution: To get the number of balls that are neither the bat nor the tyre, determine the sum of numbers present in the region of balls that are neither part of the region of the tyre nor the bat. In the diagram given below, the shaded part represents the region common to balls but uncommon to tyres and bats.

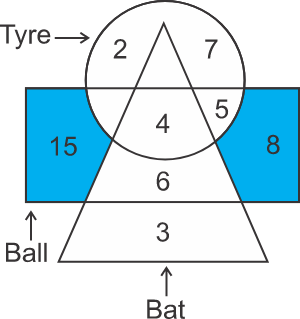
Therefore, the number is→15 + 8 = 23

So, from the above, the total number of balls that are neither tyre nor bat is 23. Hence, the third option is correct.

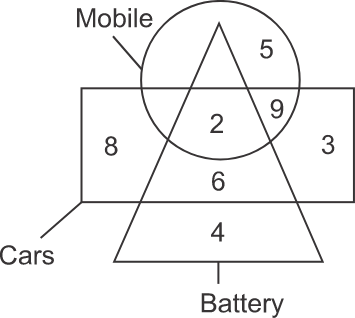
Q2. Directions: How many mobiles are not batteries?

A) 7

B) 5

C) 9

D) 14 (Correct)

Solution: To get the number of mobiles that are not batteries, determine the sum of numbers present in the region of mobiles that are not part of the region of battery. In the diagram, the shaded part represents the region common to mobiles but, uncommon to battery.

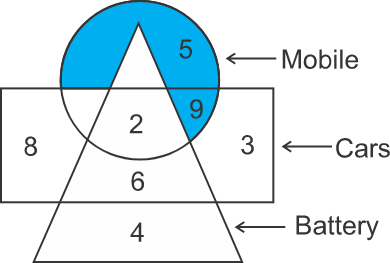
Therefore, the number is→5 + 9 = 14

So, from the above, the total number of mobiles that are not battery is 14. Hence, the fourth option is correct.

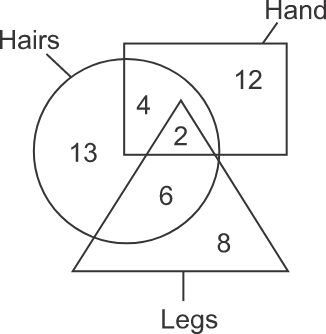
Q3. Directions: How many hands are hairs?

A) 8

B) 4

C) 6 (Correct)

D) 15

Solution: To get the number of hands that are hairs, determine the sum of the numbers falling in the part of the diagram where the regions represent hands and hairs. In the below diagram, the shaded part represents the region common to both hands and hairs as well as legs. The numbers of the asked fields that fall in the region of legs will also be counted as there is no direction given that the region belonging to legs can not be included.

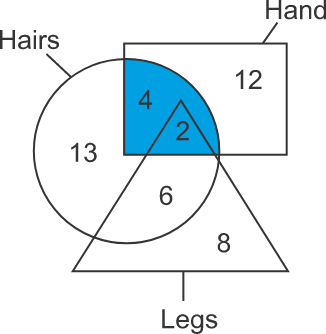
Therefore, the number is→4 + 2 = 6

So, from the above, 6 hands are hairs. Hence, the third option is correct.

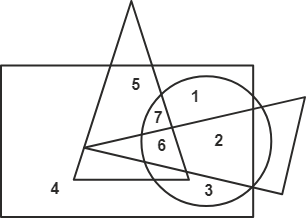
Q4. Directions: Which number is present only in one geometrical figure?

A) 3

B) 2

C) 5

D) 4 (Correct)

Solution: We need to pick the number which falls under only one of the given geometrical figures.

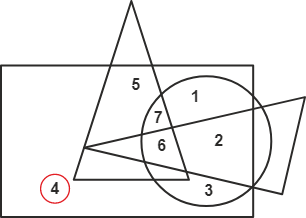
Here, 4 falls only under the rectangle's boundary in the given figure. Hence, the fourth option is correct.

Q5. Directions: In the following diagram, the triangle represents doctors, the circle represents players and the rectangle represents singers. Which region represents doctors who are singers but not players?

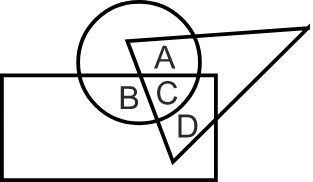
A) A

B) B

C) C

D) D (Correct)

Solution: Based on the given information in the question figure, we need to identify the letter that appears only in the area of the figures representing doctors and singers, i.e., triangle and rectangle, respectively. The highlighted part in the figure represents the doctors who are singers but not players.

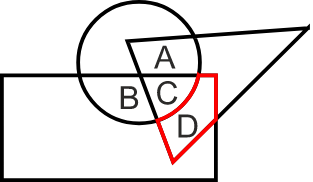
So, D is the region that represents doctors who are singers but not players. Hence, the fourth option is correct.

Venn Diagram Reasoning Questions for AP ICET/ IBSAT

1) Directions: In the following figure, the square represents philosophers, the triangle represents police officers, the circle represents pharmacists and the rectangle represents Americans. Which set of letters represents Americans who are police officers?

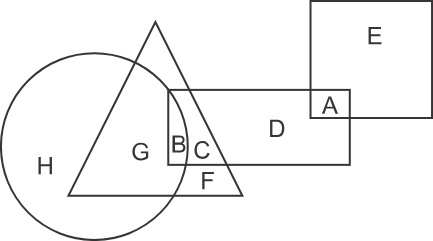
1) G, F, D, A

2) B, C

3) C, D

4) B, C, G, F

Hint: Focus on the overlapping region to both Americans and police officers.

Solution

In the below diagram, the shaded part represents the region common to both Americans and police officers as well as pharmacists. The numbers of the asked fields that fall in the region of pharmacists will also be counted as there is no direction given that the region belonging to pharmacists can not be included.

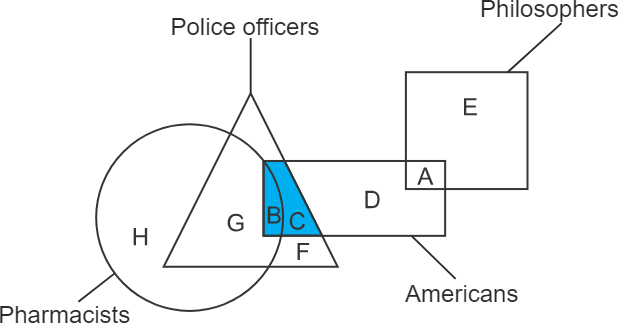
Therefore, the letters that represent Americans who are police officers are B and C. Hence, the second option is correct.

2) Directions: Which of the following diagrams represents the relationship among Complex numbers, Integers, and Natural numbers?

1)

2)

3)

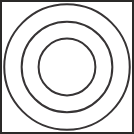
4)

Hint: Observe the given terms and think about the most suitable Venn diagram given in the options.

Solution

Based on the general information all natural numbers are integers and all integers are complex numbers. Natural numbers start from 1 and go to infinity. Integer includes all natural numbers, zero and negative numbers. Complex numbers include all integers and imaginary numbers.

Using this information, the Venn diagram will be –

Hence, the third option is correct.

Venn Diagram Reasoning Questions for KMAT/ UPESMET/ JIPMAT

1) Directions: In the following figure, the square represents therapists, the triangle represents geneticists, the circle represents yoga practitioners and the rectangle represents fathers. Which set of letters represents yoga practitioners who are neither geneticists nor fathers?

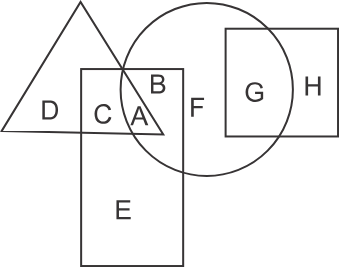
1) C, B

2) E, A

3) G, C

4) F, G

Hint: Consider those letters falling in the region of yoga practitioners which are not part of the regions of fathers and geneticists.

Solution

In the diagram, the shaded part represents the region common to yoga practitioners but, uncommon to fathers and geneticists.

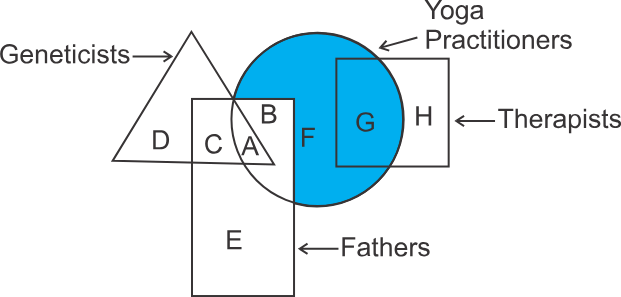
Therefore, the letters that represent yoga practitioners who are neither geneticists nor fathers are F and G. Hence, the fourth option is correct.

Read More: The verbal reasoning topics given below:

Venn Diagram Reasoning Questions for SSC CHSL/ SSC Stenographer/ SSC CGL/ SSC CPO exams

1) Directions: Select the Venn diagram that best illustrates the relationship between the following classes.

Graduates, Educated, and Unemployed

1)

2)

3)

4)

Solution

As we know educated are the ones who go to educational institutions to acquire academic qualifications. So, we can say that all graduates will be educated because without acquiring a degree the person cannot be called graduate. On the other hand, not all educated people or graduates need to be employed because some might go for higher studies, or might contribute towards social work. So, some graduates/educated may be employed some may be unemployed. Therefore, the circle of graduates lies inside the circle of educated and the circle of unemployed intersects the circle of graduates and educated.

So, according to the above information, the Venn diagram will be as follows –

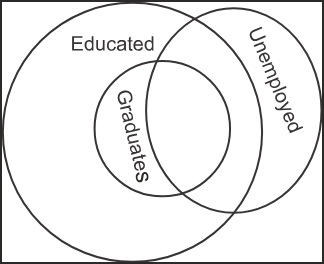
Hence, the second option is correct.

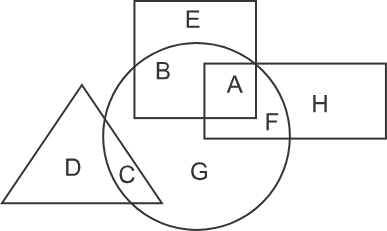
2) Directions: In the following figure, the square represents Pharmacists, the triangle represents Singers, the circle represents Surgeons and the rectangle represents Mothers. Which set of letters represents Surgeons who are either Mothers or Singers?

1) E, D, G

2) A, F, C

3) A, D, C

4) H, B, C

Hint: Make a set of the letters falling in the overlapping region between Surgeons and Mothers as well as between Surgeons and Singers.

Solution

In the diagram, the shaded part represents the overlapping region between Surgeons and Mothers as well as the overlapping region between Surgeons and Singers. Letters falling in the region of Pharmacists will also be considered in the case of overlapping as there is no restriction given on it in the question.

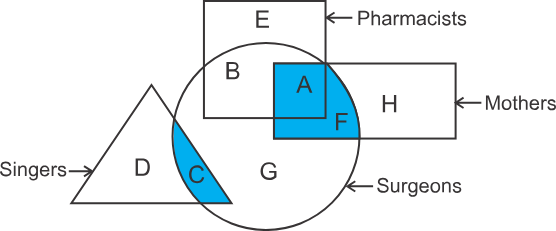
Therefore, the set of letters that represent surgeons who are either mothers or singers are A, F, and C. Hence, the second option is correct.

Venn Diagram Reasoning Questions for IBPS CWE Clerical/ IBPS RRB Assistant/ Railway Recruitment Board exams

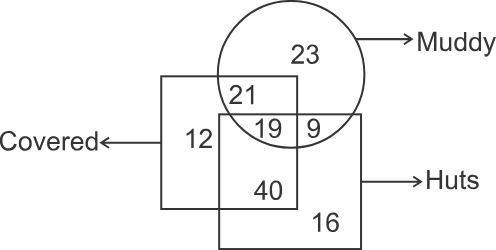
1) Directions: In the given figure, how many huts are covered and muddy?

1) 28

2) 40

3) 33

4) 19

Hint: Get the number falling in that part of the diagram where the region represents huts that are both covered and muddy.

Solution

According to the question, need to find the region which is common to muddy, covered, and huts. In the diagram, the shaded part represents the region common between huts, covered and muddy.

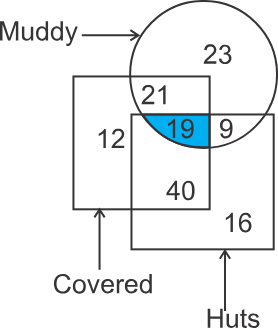
Therefore, the number of huts that are covered and muddy is 19. Hence, the fourth option is correct.

For non verbal reasoning read the topics below:

About the Faculty
Tanu Gupta, with over a decade of experience as a reasoning faculty, specializes in preparing students for various entrance examinations and career development. Her extensive work with multiple educational platforms and institutions has honed her expertise in logical and analytical thinking. Her dedication to innovative teaching methods ensures these articles provide practical insights and expert guidance.