SHM Full Form
What is the full form of SHM?
SHM stands for Simple Harmonic Motion. It is a type of periodic motion in which an object oscillates around a fixed point (called the equilibrium position) in a regular and repetitive manner. Simple harmonic motion is characterized by the fact that the restoring force acting on the object is always proportional to the displacement of the object from the equilibrium position, and acts in the direction opposite to the displacement.
Periodic motion
In physics, a periodic motion is defined as a motion that repeats itself after a fixed interval of time. In other words, it is a repetitive motion that repeats itself in equal intervals. We can find various real-life motions that are periodic; these are a swing in motion, revolution and rotation of the earth, hands or needles of the clock/watch, etc.
The time at which the motion is repeating itself is called the period (or time period), denoted by T, while the number of periods per unit of time is called frequency. It is denoted by \nu ![]() and has the unit s^{-1}
and has the unit s^{-1} ![]() . For example, if the motion is repeating itself every ten seconds, then the time period and frequency will be;
. For example, if the motion is repeating itself every ten seconds, then the time period and frequency will be;
\begin{aligned}
\text{Time Period T = 10s}\\
\Rightarrow \text{Frequency } \nu = \frac{1}{T}\\
\Rightarrow \nu = \frac{1}{10} = 0.1 \ s^{-1}
\end{aligned}
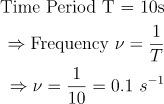
Simple Harmonic Motion
Simple Harmonic Motion, or simply SHM, is a type of periodic motion, specifically oscillatory motion, which is governed by restoring force. Restoring force is the force acting opposite to the displacement such that the system will be in equilibrium.
The simple harmonic motion follows Hooke’s Law, which says that the restoring force applied to work against the displacement so that equilibrium is attained is directly proportional to the displacement caused due to the applied force. In mathematical terms,
\begin{aligned}
&\text{Restoring Force} \propto \text{Displacement}\\
& \Rightarrow F \propto -x \\
& \Rightarrow F = -kx \\
\end{aligned}
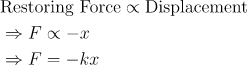
The following can also be written in terms of acceleration. Thus, we can also write;
\begin{aligned}
& \Rightarrow a \propto -x \\
& \Rightarrow a = - \omega^2 x
\end{aligned}
![]()
Key terms for SHM
For describing the characteristics of SHM, we consider a system of a simple pendulum which has mean and extreme positions such that we have the following key terms.
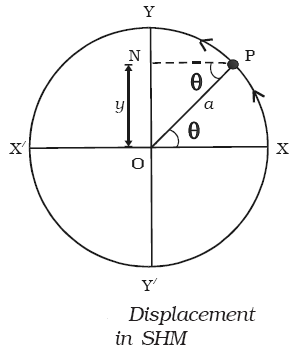
Displacement: Displacement is the distance of a particle between its mean to the extreme position. For a simple pendulum, we have two displacement components, x \text{ and } y ![]() . For the given figure, we have the following;
. For the given figure, we have the following;
\begin{aligned}
& y=a \sin (\theta)\\
& x=a \cos (\theta)
\end{aligned}
![]()
For \theta = \omega t ![]() and phase difference \phi
and phase difference \phi ![]() , we can write the displacement as;
, we can write the displacement as;
\begin{aligned}
& y=a \sin (\omega t + \phi)\\
& x=a \cos (\omega t + \phi)
\end{aligned}
![]()
Amplitude: It is the maximum displacement of the simple harmonic motion. It is denoted by ‘a’. In SHM, if \theta = \frac{\pi}{2} ![]() , then the displacement along y-axis will be,
, then the displacement along y-axis will be,
y= a \sin (\frac{\pi}{2}) = a
![]()
And if \theta = 2\pi ![]() , then the displacement along the x-axis will be,
, then the displacement along the x-axis will be,
x= a \cos (2\pi) = a
![]()
Velocity: It is the rate of change of displacement of the simple harmonic motion. For the simple harmonic motion, the velocity will be as follows;
\begin{aligned}
& y = a \sin (\omega t)\\
& \text{Velocity, } v = \frac{dy}{dt} = \frac{d(a \sin (\omega t))}{dt}\\
& \Rightarrow v = a \omega \cos (\omega t)\\
& \Rightarrow v = a \omega \sqrt{1-\sin^2 (\omega t)}\\
& \Rightarrow v = a \omega \sqrt{1- \frac{y^2}{a^2}}\\
& \Rightarrow v = \omega \sqrt{a^2 - y^2}\\
\end{aligned}
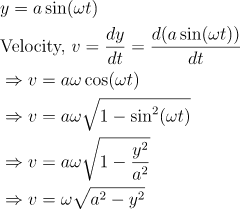
Acceleration: It is the rate of change of velocity of the simple harmonic motion. In the simple harmonic motion, the acceleration is calculated as;
\begin{aligned}
& y = a \sin (\omega t)\\
& \text{Acceleration, } a = \frac{dv}{dt} = \frac{d^2y}{dt^2}\\
& \Rightarrow Acceleration = \frac{d^2(a \sin (\omega t))}{dt^2} \\
& \Rightarrow Acceleration = - a \omega^2 sin (\omega t)\\
& \Rightarrow Acceleration = - \omega^2 y\\
\end{aligned}
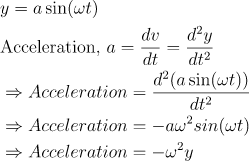
Time period: It is the time at which the simple harmonic motion will repeat itself. The time period for the simple harmonic mission is;
\begin{aligned}
& \text{Time Period T} = \frac{2\pi}{\omega} = \frac{2\pi}{\sqrt{a/y}} = 2\pi \sqrt{\frac{\text{displacement}}{\text{acceleration}}}\\
\end{aligned}
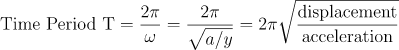
Frequency: It is the reciprocal of the time period. It can be calculated as;
\begin{aligned}
& \text{Frequency } \nu = \frac{1}{T} = \frac{1}{2\pi} \sqrt{\frac{\text{acceleration}}{\text{displacement}}}\\
\end{aligned}
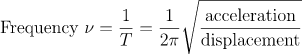
Frequently Asked Questions (FAQs)
Frequency is the reciprocal of the time period.
It is the measure of the rate of change in the angular displacement.
v = \omega a ![]() will be the maximum velocity of the SHM at the extreme position of the simple pendulum.
will be the maximum velocity of the SHM at the extreme position of the simple pendulum.
The displacement of SHM is maximum and equal to the amplitude when \sin \theta \text{ and } \cos \theta ![]() will be unity.
will be unity.
It is defined as a motion which does not repeat itself in a fixed time interval.