Surface Counting: Techniques and Practice for Design Entrance Exams

Surface counting is a visualization exercise that involves determining the number of distinct surfaces in a three-dimensional object. Mastering surface counting enhances spatial reasoning and analytical abilities, which are essential for success in Design aptitude examinations. These skills are frequently tested in design entrance exams such as NID and UCEED, where candidates are required to analyze and interpret complex geometric structures.

This Story also Contains

1. INTRODUCTION TO SURFACE COUNTING
2. Understanding the Concept of Continuity and Discontinuity :
3. Practice Questions for Surface Counting:

INTRODUCTION TO SURFACE COUNTING

Surface counting involves counting the number of visible and invisible surfaces for a given three-dimensional arrangement. A three-dimensional arrangement could be a single entity or a combination of more than one three-dimensional volume with continuity or discontinuity in the surfaces, which we would go through next :

1.Discontinuous Surfaces : Cube and Cuboid

To understand the fundamentals of Surface Counting for 3D volumes, we will begin with the primary volumes like cubes and cuboids.

Cube (all sides are equal)

Both cube and cuboid have 06 surfaces, considering the volumes length, width and height.

Top: 01

Bottom: 01

Sides: 04

2. Continuous Surface : Sphere

A sphere, even with an equal/smaller or greater volume than a cube, has one continuous surface.

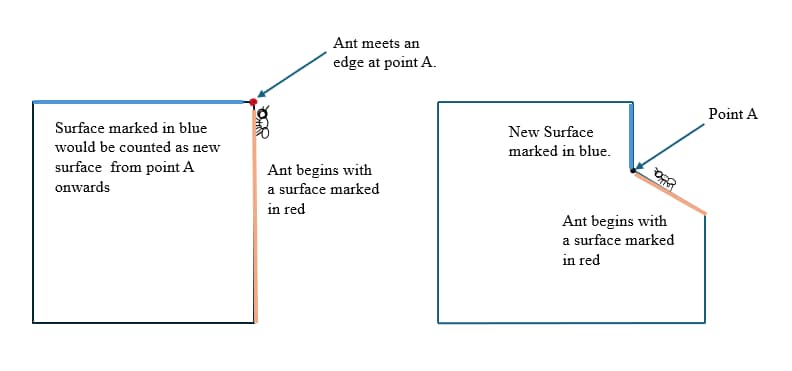
Activity : How to Count the Surfaces ?

Trick: Suppose an ant starts travelling across a surface, at point A, it meets an edge while travelling the surface. From Here(point A), the surface would be counted as the second surface.

Students may also check:

These are some of the topics that are generally also asked in DAT exams. Students can go through for their design entrance exam preparations.

• Mirror and Water Images for Design Entrances Exams
• Surface Counting: Advanced Level Techniques and Strategies

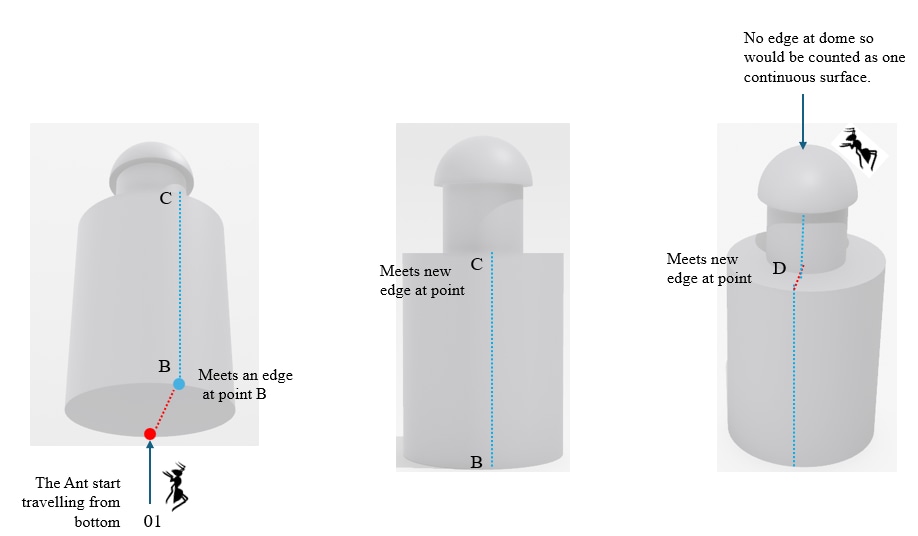
Concept 01: The Ant Rule

Imagine an ant travelling along the edges of a wall.

For the above figure, Count the Number of surfaces for the given volume, as inferred from the two given views using the “Ant Rule”.

Solution: 06 Surfaces

Method: Ant travelling across the edges

Description: As per the Ant Rule, at every encounter of an edge, the following surface count would be a new surface.

To Start counting, we need to understand the logic for solving such questions.

Logic 01: Continuity or discontinuity of a surface, marked by edge. In a question, the figure may contain two or more geometric volumes combined, as simple as a combination of cubes to a complex combination of multiple volumes, as shown in the above figure, which combines cylinders and hemispheres. In such cases, the edge serves as a partition between two surfaces.

Understanding the Concept of Continuity and Discontinuity :

Logic 02: Direction

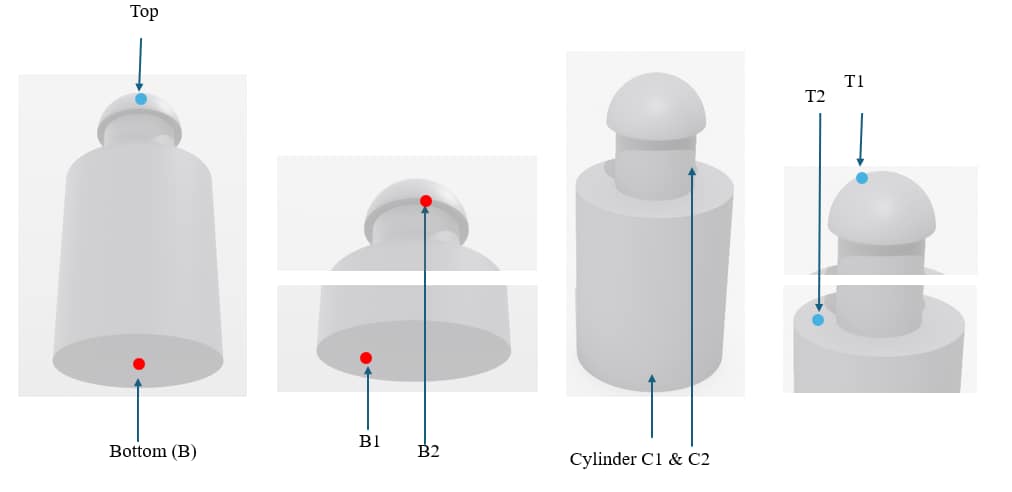
It is a good practice always to count all the surfaces visible from a given direction(like the top) out of 06 possible directions.

For example, all the surfaces visible from the top should be counted at a time in the figure, i.e., T1 & T2.

How To: Select a Direction to begin counting the surfaces.

Step-by-Step Approach to Solution

• Step 01: Choose any one direction, only the Top or Only the bottom, to begin. In the given figure, we start with the bottom approach.
• Step 02: Count all the visible surfaces from the bottom, as shown in Figure 02
• Step 03: Count all the Right-side surfaces. In this case of cylindrical surfaces, only C1 & C2
• Step 04: Count all the visible surfaces from the top, in this case, T1 & T2

TOTAL SURFACES

B1+B2+C1+C2+T1+T2 = 6 surfaces

Practice Questions for Surface Counting:

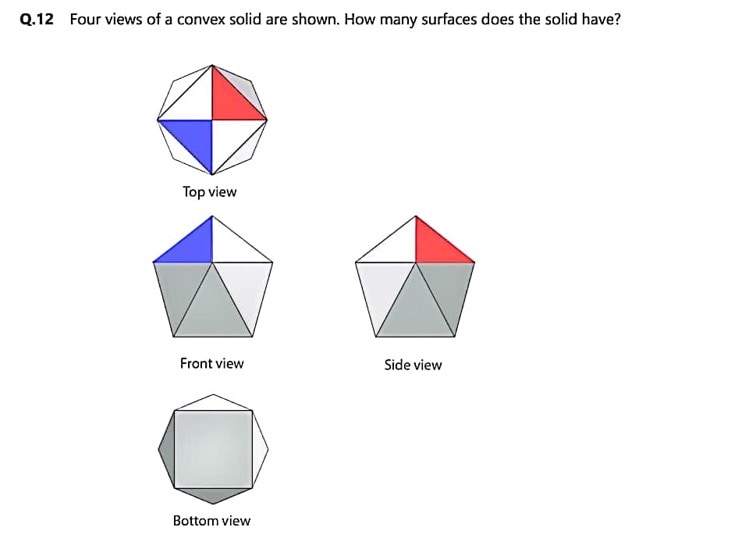
Solution:

• Top View: The top view shows a triangular face (red and blue) with the edges of the base.
• Front View: The front view shows the shape with one triangle at the top, two triangular sides, and the base.
• Side View: The side view shows one triangular face and some of the base.
• Bottom View: The bottom view reveals the base of the polyhedron, confirming that the solid has multiple triangular faces and a square or rectangular base.

Therefore, total surfaces for above figure will be-11.

Q 2 : A pentagonal shape is cut out from the sphere for the given figure. Count the number of surfaces in the newly formed 3D volume.

Solution: The given figure shows a sphere with a pentagonal shape cut out from it. In this scenario, the number of surfaces in the newly formed 3D volume can be calculated as follows:

1. The sphere initially has 1 curved surface.
2. After the pentagonal cut, the flat pentagonal surface is created, which adds 1 new surface.
3. The curved surface of the sphere is now divided into multiple segments, and each of these segments creates new surfaces. Since the cut creates a pentagonal hole, this adds 5 new surfaces where the cuts meet the sphere.

Thus, the total number of surfaces in the newly formed 3D object is:

1 (curved surface) + 1 (flat pentagonal surface) + 5 (cut surfaces) = 7 surfaces.

Therefore, the correct answer is 7 surfaces.

Q 3 : From the Front, Right side and Perspective views for the given volume, Count the number of faces in the figure.

Hint: Count all the faces from one side in one go, e.g. counting all the visible surfaces from the right side view.

Solution: To count the number of faces in the given volume, you can follow these steps:

1. Front View: Count all the visible surfaces (front faces) from this view.
2. Right Side View: Count all the visible surfaces (side faces) from this perspective.
3. Perspective View: Check for the three-dimensional depth and any hidden or visible surfaces not visible in the other two views.

Now, for the front view, and the perspective view, you can repeat a similar process. The general approach is to identify the visible parts and edges that form faces.

• The 2 side faces of the box.
• The bottom face.
• The cylindrical face, which is visible through the hole.

Therefore, the correct answer is 6 surfaces.

Students can also refer to the below articles:

• Fundamental Geometry Concepts for 2D Shapes
• Color Theory, Color Wheel for Designers
• Spatial Ability - Block Counting