Degenerate Orbitals - Explanation with Diagram, Examples, FAQs

What is a degenerate orbitals?

Those orbitals are said to be degenerate which have same energy levels are called degenerate orbitals. In chemistry degenerate meaning is when one energy level corresponds to two or more states of motion. These degenerate orbitals exist at all times unless the magnetic field is disrupted. The application of the magnetic field is disrupted by the degeneracy.

Degenerate definition

The orbitals having same energy levels are called degenerate orbitals.

Before discussing about degenerate orbitals we first have to study about Aufbau principle, Pauli exclusion principle and Hund’s rule.

Also read -

• NCERT Solutions for Class 11 Chemistry
• NCERT Solutions for Class 12 Chemistry

• NCERT Solutions for All Subjects

Aufbau Principle: The Aufbau principle governs how electrons are filled in an atom's atomic orbitals when it is in its ground state. This theory mentioned that electrons are filled into their atomic orbitals in sequence and that sequence is according to their increasing orbital energy level. According to the Aufbau principle it is stated that those orbitals which have lowest energy are occupied first and those who had higher energy levels will occupied thereafter.

The word 'Aufbau' has German meaning or we can say is derived from German word have the meaning 'build up' or 'construct.' The order in which atomic orbitals are filled is depicted in the diagram below. The primary quantum number is ‘n,' and the azimuthal quantum number is ‘l.' The Aufbau principle can also be used to figure out where electrons are in an atom and what energy levels they correspond to.

The arrangement of electrons on the basis of Aufbau principle can be shown as follows:

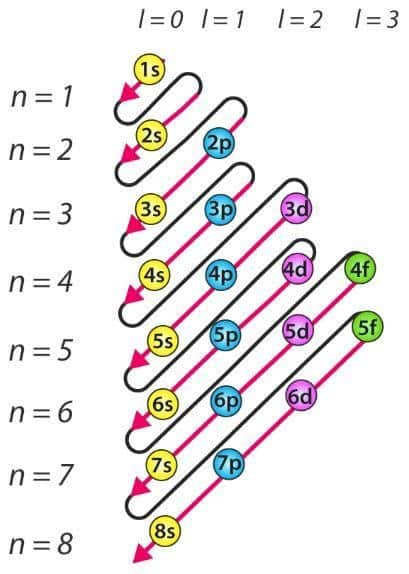
The main features of Aufbau principle can be described as:

• The Aufbau principle states that electrons will filled in the lowest-energy orbitals first. This suggests that electrons can only enter in higher-energy orbitals after it will be entirely filled in lower-energy orbitals.
• The (n+l) rule can be utilized to start a sequence where the energy of orbitals grow along with the addition of primary quantum number and azimuthal quantum number which determines the energy level of orbitals.
• Lower orbital refers to lower (n+1) values. When two orbitals possess same (n+1) values, the orbital having lower n value will have less energy.
• Order of orbitals in which they filled will be 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p…. this is shown in the image.

Pauli Exclusion Principle:

The Pauli Exclusion Principle states that only two electrons are there in a single atom more than two atoms in single electron is not possible and those two atoms will contains the same set of quantum numbers given by n, l, ml, and ms. To put it another way, each electron should have or be in its own distinct state (singlet state). The Pauli Exclusion Principle is basically explained with the help of two principles:

• It is stated that at same time only two electrons are possible to be in the same orbital.
• The spins of the two electrons in the same orbital must be opposing or they must be anti parallel.

Pauli's Exclusion Principle, on the other hand, does not simply apply to electrons. It also applies to fermions and other half-integer spin particles. It is irrelevant for particles having an integer spin, such as bosons, because their wave functions are symmetric. Like fermions bosons also said to have the same quantum states. The Bose-Einstein distribution function, on the other hand, is where bosons derive their name.

Hund’s rule:

The Aufbau principle states that electrons fill those orbitals first which have lowest energy. The electrons move on to higher energy orbitals after the lower energy orbitals are occupied. The difficulty with this rule is that it leaves out information on the three 2p orbitals and their filling sequence.

Hund's rule is as follows:

• Every orbital in the sub level is singly occupied prior to the double occupation of any orbital.
• All electrons in a single occupancy orbital have the same spin in order to maximise overall spin.

It is mentioned that an electron which has the ability to fill all of its orbitals who have similar energy they will not be able to pair up with another electron in a half-filled orbital. Atoms present in the ground state will contains a large number of unpaired electrons and when any of these two electrons come in contact with each other then it behaves similar towards two magnets like Before they tried to attracted to each other the electrons will repel each other i.e. they want to go apart from each other as much as possible.

Hence these three rules states that how electrons will be distributed to any orbital and those orbitals which contains to have same energy level are said to be degenerate in nature this can be explained as follows through an example:

Also Read:

• NCERT solutions for Class 11 Chemistry Chapter 2 Structure of Atom
• NCERT Exemplar Class 11 Chemistry Solutions Chapter 2 Structure of Atom
• NCERT notes Class 11 Chemistry Chapter 2 Structure of Atom

Degenerate orbitals example:

Like if we talk about s sub shell then it attains only two electrons which follow Hund’s rule that one of them is parallel and other one is anti-parallel in nature which means they both have opposite spins of value +1/2 or -1/2 for clockwise or anti-clockwise respectively. There are three degenerate orbitals in the p orbital and all these three p orbials have contains the same amount of energy. At start, only one electron is assigned to each orbital. The second electron will have the opposite spin as the first. There are six electrons in total because each orbital is filled.

Degenerate orbitals which exist in the 2p sublevel will have the 2px, 2py, and 2pz orbitals all have the same energy while the 3px, 3py, and 3pz orbitals are also said to be degenerate orbitals. The 3dxy, 3dxz, 3dyz, 3dx2 – y2, and 3dz2 are degenerate orbitals having the same energy at the 3d energy level. On the other hand if we talk about f-orbitals then it splits into 7 orbitals.

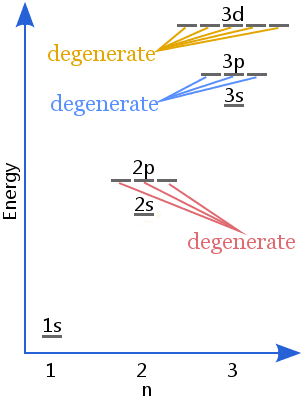
Degeneracy refers to the total number of distinct states of the same energy. Degeneracy is also known by the other name called degree of degeneracy.

Hence from the above discussion we can say that the degeneracy for p orbitals is 6 as it can accommodate maximum of 6 electrons, for d orbitals it would be 5 as d orbitals can attain maximum of 10 electrons and for f orbitals degree of degeneracy is 14 as it can accommodate maximum of 14 electrons.

Also check-

• NCERT Exemplar Class 11th Chemistry Solutions
• NCERT Exemplar Class 12th Chemistry Solutions
• NCERT Exemplar Solutions for All Subjects

NCERT Chemistry Notes:

• NCERT Notes Class 11th Chemistry
• NCERT Notes Class 12th Chemistry
• NCERT Notes For All Subjects