Frequency, Time Period And Angular Frequency

Time Period and Frequency of Revolution of an Electron in the n^th Bohr orbit

As the spectroscopists, the time-period and frequency of an electron’s revolution in the n^th Bohr orbit are basic necessary parameters in chemistry. Niels Bohr’s atomic model introduced the concept of orbits in which electrons revolve in circles around the nucleus and each orbit is defined by a number called the principal quantum number (n). The time-period (T_n) is the time taken by a particular electron to revolve in a particular orbit and can be determined as:

($T_n=\frac{2 \pi r_n}{v_n}$), where ($r_n$) is the radius of the nth orbit and ($v_n$.) is the velocity of the electron in that orbit

On the other hand, frequency [fn] is defined as the number of vibrations per second or the number of complete oscillations per second, it is connected with the difference in energy levels between the concerned orbits. These concepts are very vital in spectroscopy, whereby they determine the emission and absorption of photons which correspond to energy transitions. They also determine the stability of the atomic nucleus as well as the chemical activity, giving details on the status of elements and molecules.

Although the precise equations for the time period and frequency of revolution are not required, it is still a good idea to look at the variations of these with the atomic number (Z) and the orbit number (n).

We know that Time period (T) is the time required for one complete revolution and that Frequency (f) is the inverse of the time period.
The time period (T) of an electron in the nth Bohr orbit is proportional to $\mathrm{n}^3 / \mathrm{Z}^2$ (where n is the principal quantum number and Z is the atomic number), and the frequency (f) of revolution is proportional to $Z^2 / n^3$. This means the time period increases with the cube of the principal quantum number, while the frequency decreases with the cube of the principal quantum number.
$\begin{gathered}\therefore T=\frac{\text { distance }}{\text { time }}=\frac{2 \pi r}{v} \\ \because \mathrm{r} \propto \frac{\mathrm{n}^2}{\mathrm{Z}} \text { andv } \propto \frac{\mathrm{Z}}{\mathrm{n}} \\ \therefore T \propto\left(\frac{n^2}{Z} \times \frac{n}{Z}\right) \propto\left(\frac{n^3}{Z^2}\right) \\ \therefore v=\left(\frac{1}{T}\right) \propto\left(\frac{Z^2}{n^3}\right)\end{gathered}$

You must remember all the above formulas and relations.

Also Read:

• Electronic Configuration Of Elements
• Stability Of Orbitals: Half-filled And Completely-filled

For a better understanding of the topic and to learn more about Frequency, Time Period And Angular Frequency with video lesson, the link has been provided below:

Recommended YouTube video (Frequency, Time Period And Angular Frequency):

Solved Examples Based on Time Period and Frequency of Revolution of an Electron in the n^th Bohr Orbit

Example 1: Ratio of frequency of revolution of the electron in the 2nd excited state of He+and 2nd state state of hydrogen is.

1) $\frac{32}{27}$

2) $\frac{27}{32}$
3) $\frac{1}{54}$

4)$\frac{27}{2}$

Solution:

$
\begin{aligned}
&\begin{gathered}
\frac{f_1}{f_2}=\frac{z_1^2}{n_1^3} \times \frac{n_2^3}{z_2^2} \\
\Rightarrow n_1=3, n_2=3, z_1=2, z_2=1
\end{gathered}\\
&\therefore \text { putting these value in the equation we get }\\
&\frac{2^2}{3^3} \times \frac{2^3}{1}=\frac{32}{27}
\end{aligned}
$

Hence, the answer is the option (1).

Example 2: The time taken for an electron to complete one revolution in the Bohr orbit of the hydrogen atom is

1) $\frac{4 \pi^2 m r^2}{n h}$
2) $\frac{n h}{4 \pi^2 m r}$
3) $\frac{n h}{4 \pi^2 m r^2}$

4) $\frac{h}{4 \pi m r}$

Solution:

We know that time period is the time taken for one complete revolution.

$T=\frac{2 \pi r}{V}$(1)

Now, we know that the angular momentum of an electron in $n^{\text {th }}$ orbit is given by $m V r=\frac{n h}{2 \pi} \Rightarrow V=\frac{n h}{2 \pi m r} \ldots \ldots$

From equations (1) and (2),

$
\therefore T=\frac{2 \pi r}{V}=\frac{2 \pi r}{\frac{n h}{2 \pi m r}}=\frac{4 \pi^2 m r^2}{n h}
$

Hence, the answer is the option (1).

Example 3:Determine the frequency of revolution of the electron in 3^rd Bohr's orbit in hydrogen atom:

1) 0.024 x 10¹⁶Hz

2) 3.4 x 10¹⁶Hz

3) 8.13 x 10¹⁶Hz

4) 0.054 x 10¹⁶Hz

Solution:

As we have learnt,

Frequency = 1/(Time period)

Period = Total distance covered/velocity

= 2πr/v

Thus, frequency = v/2πr

Now, velocity of electron in 3rd Bohr’s orbit = 2.16 x 10⁶(1/3)m/s

= 0.72 x 10⁶m/s

And, radius of 3rd Bohr’s orbit $=0.53 \times 10^{-10}\left(3^2 / 1\right)$

$=4.77 \times 10^{-10} \mathrm{~m}$

Now, frequency = $=\mathrm{v} / 2 \pi \mathrm{r}$

$=0.72 \times 10^6 \mathrm{~m} / \mathrm{s} /\left(2 \times 3.14 \times 4.77 \times 10^{-10} \mathrm{~m}\right)$

$=0.024 \times 10^{16} \mathrm{~Hz}$

Hence, the answer is the option (1).

Example 4: The ratio of the orbital frequency of electron of hydrogen in the 3^rd and 2^nd orbital is:

1) 3.37

2) 0.29

3) 0.44

4) 2.25

Solution

We know that,

Frequency $\propto \frac{\mathrm{Z}^2}{\mathrm{n}^3}$
For the same value of $Z$,

$
\begin{gathered}
f \propto \frac{1}{n^3} \\
\frac{f_3}{f_2}=\frac{\frac{1}{3^3}}{\frac{1}{2^3}}=\frac{8}{27}=0.29
\end{gathered}
$

Hence, the answer is the option (2).

Example 5:

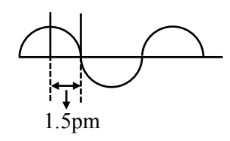
A hypothetical electromagnetic wave is show below.

The frequency of the wave is $\mathrm{x} \times 10^{19} \mathrm{~Hz}$. $x=$ $\qquad$ (nearest integer).

[JEE Main 2024]

Solution:

$\begin{aligned} \lambda & =1.5 \times 4 \mathrm{pm} \\ & =6 \times 10^{-12} \text { meter } \\ \lambda v & =\mathrm{C} \\ 6 & \times 10^{-12} \times v=3 \times 10^8 \\ v & =5 \times 10^{19} \mathrm{~Hz}\end{aligned}$

Hence, the answer is (5).

Practice More Questions From the Link Given Below:

Conclusion

Finally, It is comprehensible and quite reasonable that two of the most important concepts in atomic structure and atomic behaviour are the time period and frequency of revolution of the electrons in Bohr orbits. Niels Bohr’s model was essential in giving a foundation for a concept which stated that electrons orbit in a particular path with fixed energies. Regarding these orbits, two quantitative parameters known as the time period and the frequency affect atomic spectra, which show various lines for energy transitions. These parameters are basic in spectroscopy where the kinds of elements and composition of chemicals by emitted or absorbed radiation are determined. Also, they stress atomic stability, asserting that transitions between energy levels determine chemical activity and bonding characteristics. In addition to theoretical significance, knowledge about electron orbits improves technological advancements, like lasers and quantum computing, based on specific energy changes. Hence one can deduce an understanding of time-period and frequency concerning Bohr orbits that enhances understanding of atomic physics and stimulates improvement in fields of science as well as technology.