Absolute and Relative Error- Definition, Formulas, and Examples
Measurements are one of the most important parts of scientific computing. Absolutely accurate measurement results are very rare. Small errors are common when measuring different parameters. There are various types of errors that lead to measurement errors. Each and every error can be expressed mathematically. If we know the error, we can find a way to calculate it correctly and fix the error. There are two main types of error: absolute error and relative error. This article defines absolute and relative errors. Descriptions, formulas, and examples of absolute and relative errors are given here, along with their definitions. Knowledge of various errors is necessary for the measurement.
This Story also Contains
- Absolute Error
- Formula For Absolute Error
- Example Of Absolute Error
- Relative Error
- Formula For Relative Error
- Example Of Relative Error
Absolute Error
The difference between actual quantity and measured quantity is known as absolute error. Importance of these types of errors totally depends on the types of quantity measured. As we know that street distance is very large so, a very small error if comes in measurement will be ignored. A centimeter error is significant when measuring the length of mechanical parts. In both cases, the error is very small (in centimeters), but the error in the second case is more significant.
Commonly Asked Questions
Q: What is absolute error in mathematics?
A:
Absolute error is the difference between the measured or approximated value and the actual or true value of a quantity. It gives us an idea of how far off our measurement or approximation is from the real value, regardless of whether it's an overestimate or underestimate.
Q: Can absolute error be negative?
A:
No, absolute error is always positive or zero. It represents the magnitude of the difference between the measured and actual values, regardless of whether the measurement is an overestimate or underestimate.
Q: What's the difference between absolute error and absolute deviation?
A:
Absolute error is the difference between a measured value and the true value, while absolute deviation is the difference between a value and the mean of a set of values. Absolute error requires knowing the true value, while absolute deviation is used in statistical analysis of data sets.
Q: How do absolute and relative errors factor into error bars on graphs?
A:
Error bars can represent either absolute or relative errors. Absolute error bars have a constant length regardless of the data point's value, while relative error bars scale with the value of each data point.
Q: Why might we prefer to use absolute error in some situations and relative error in others?
A:
Absolute error is useful when we're dealing with measurements in the same units and scale, allowing direct comparisons. Relative error is preferable when comparing measurements of different magnitudes or even different quantities, as it provides a standardized measure of error.
Formula For Absolute Error
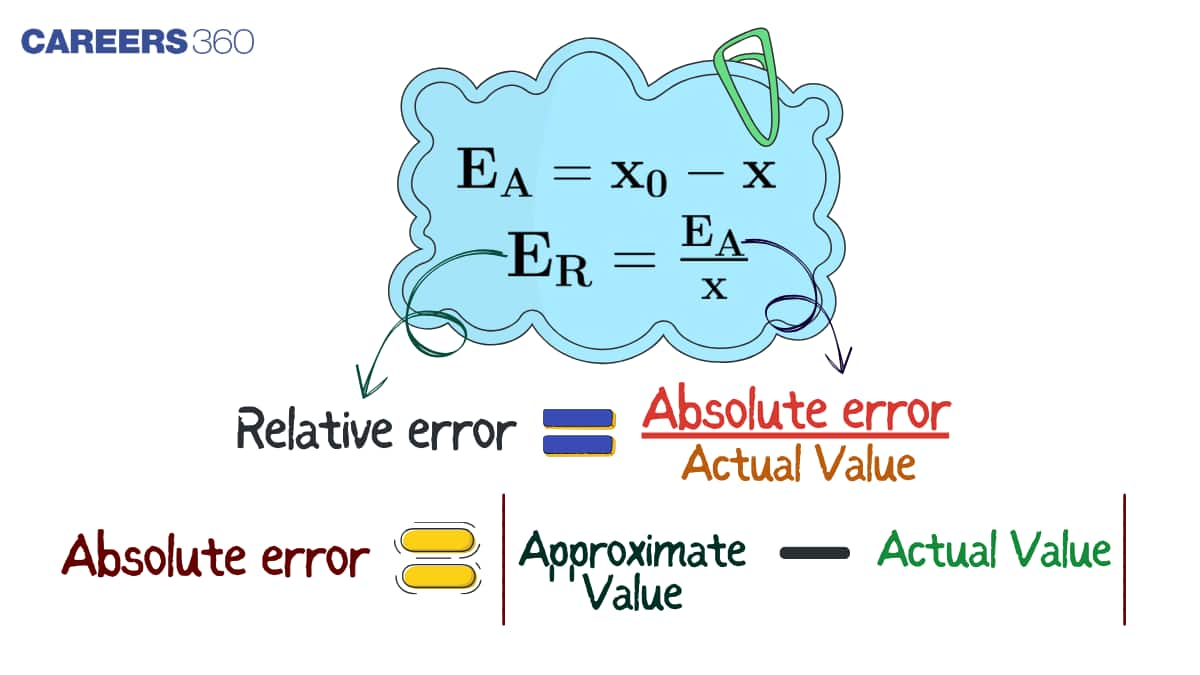
Absolute error is calculated by taking the absolute difference between the expected value of the quantity and the actual measured value.
Suppose actual measured value is M and expected value is E then absolute error is equal to absolute value of E minus M i.e, |E-M|. We have to note that,
Absolute error is always positive as it is the absolute value of the difference.
Here, the expected value can also be mentioned as theoretically calculated value or value mentioned in books, features, etc.
Commonly Asked Questions
Q: What's the formula for calculating absolute error?
A:
The formula for absolute error is: |Measured Value - Actual Value|. The vertical bars indicate that we take the absolute value of the difference, ensuring the result is always positive.
Q: How do rounding and truncation affect absolute and relative errors?
A:
Rounding and truncation introduce additional errors into calculations. They directly affect the absolute error by changing the least significant digits. This, in turn, affects the relative error, especially for small values where even small absolute changes can result in large relative errors.
Q: How do absolute and relative errors relate to the concept of tolerance in engineering?
A:
In engineering, tolerance specifies the acceptable range of variation for a measurement or characteristic. Absolute error helps determine if a measurement falls within the specified tolerance range, while relative error can be used to express tolerance as a percentage of the ideal value.
Q: How do absolute and relative errors relate to the concept of uncertainty in physics?
A:
In physics, uncertainty is often expressed as an absolute error (e.g., ±0.1 cm) or a relative error (e.g., ±2%). These errors provide a range within which the true value is expected to lie, quantifying the uncertainty in the measurement.
Q: Why is it important to consider the units when dealing with absolute error?
A:
Units are crucial for absolute error because they provide context for the magnitude of the error. An absolute error of 1 has very different implications if the units are millimeters versus kilometers. Relative error, being a ratio, is unitless.
Example Of Absolute Error
Here we take day-to-day life examples of absolute error. Suppose we have a pencil and its expected or theoretically written length is equal to 16 cm, but the actual measured length of the same pencil is 15.95 cm. Now we know that absolute error is equal to absolute value of actual measured value minus expected value of quantity.
Absolute error is equal to 16 minus 15.95 which is equal to 0.05 cm.
Commonly Asked Questions
Q: What's the relationship between absolute error and significant digits?
A:
The number of significant digits in a measurement implies a certain level of absolute error. For example, if a length is reported as 10.0 cm, it suggests an absolute error of about ±0.05 cm. More significant digits generally imply smaller absolute errors.
Q: How do absolute and relative errors relate to the concept of significant figures?
A:
The number of significant figures in a measurement implies a certain level of absolute error. For example, a measurement of 1.23 cm implies an absolute error of about ±0.005 cm. Relative error can then be calculated from this implied absolute error.
Q: How do absolute and relative errors affect the reliability of predictions made from mathematical models?
A:
Both types of errors impact the reliability of predictions. Absolute errors give an idea of how far off predictions might be in absolute terms, while relative errors indicate how significant these deviations might be relative to the predicted values. Understanding both helps in assessing the model's reliability.
Q: Why is it important to consider significant figures when discussing errors?
A:
Significant figures are important because they indicate the precision of a measurement. Reporting more significant figures than the measurement justifies can imply a level of accuracy that doesn't actually exist, potentially leading to misunderstandings about the error involved.
Q: Why is it important to report both the value and its associated error in scientific measurements?
A:
Reporting both the value and its error provides a complete picture of the measurement. The value alone doesn't indicate how precise or accurate the measurement is. The error information allows others to judge the reliability of the measurement and use it appropriately in further calculations.
Relative Error
When we divide absolute error by expected value then we get a new value which is known as relative error. In other words, it is a ratio between the absolute error and theoretically expected value. Once we calculate the relative error, we will get an idea about the accuracy of our measurement. You can also calculate absolute error if you know about the relative error. It does not have any dimension or unit. When we express relative error in percentage, it is known as percentage error.
Commonly Asked Questions
Q: How does relative error differ from absolute error?
A:
Relative error is the ratio of the absolute error to the actual value, usually expressed as a percentage. While absolute error gives the magnitude of the error, relative error provides context by showing how significant that error is compared to the true value.
Q: What's the difference between error and uncertainty in measurements?
A:
Error is the difference between a measured value and the true value, while uncertainty is an estimate of the range within which the true value is likely to fall. Error is a single value, while uncertainty is typically expressed as a range.
Q: How do absolute and relative errors help in comparing the accuracy of different measurements?
A:
Absolute errors allow us to compare measurements made in the same units and on the same scale. Relative errors, expressed as percentages, allow us to compare the accuracy of measurements across different scales or even different quantities.
Q: Why is it important to consider both absolute and relative errors in scientific experiments?
A:
Absolute errors give a concrete idea of the magnitude of the error, which is important for understanding the limitations of the experiment. Relative errors provide context, showing how significant the error is compared to the quantity being measured, which is crucial for interpreting results.
Q: Can you have a large absolute error but a small relative error?
A:
Yes, this can occur when dealing with very large numbers. For example, an absolute error of 1000 in a measurement of 1,000,000 would result in a relative error of only 0.1%.
Formula For Relative Error
It is the ratio between the absolute error and theoretically expected value.
Let absolute error equal to x and expected value equal to y and relative error is RE, then relative error RE is given by,
$RE = \frac{x}{y}$
Commonly Asked Questions
Q: How do you calculate relative error?
A:
Relative error is calculated by dividing the absolute error by the actual value and then multiplying by 100 to express it as a percentage: (|Measured Value - Actual Value| / |Actual Value|) × 100%
Q: Can you have zero absolute error but non-zero relative error?
A:
No, this is not possible. If the absolute error is zero, it means the measured value exactly matches the true value. In this case, the relative error, which is the absolute error divided by the true value, would also be zero.
Q: How does the magnitude of the measured value affect the relationship between absolute and relative errors?
A:
For a given absolute error, the relative error will be larger for smaller measured values and smaller for larger measured values. This is because relative error is the ratio of absolute error to the measured value.
Q: How do absolute and relative errors relate to accuracy and precision in measurements?
A:
Accuracy is related to how close a measurement is to the true value, which is directly measured by absolute and relative errors. Precision, on the other hand, relates to the consistency of repeated measurements and doesn't directly correspond to these errors.
Q: How do systematic and random errors affect absolute and relative errors?
A:
Systematic errors consistently skew results in one direction, affecting both absolute and relative errors. Random errors can increase or decrease measurements unpredictably, potentially canceling out over multiple trials but still contributing to overall error.
Example Of Relative Error
Here we take day-to-day life examples of absolute error. Suppose we have a pencil and its theoretically mentioned length is equal to 16 cm, but the actual measured length of the same pencil is 15.5 cm. Now we know that when we divide absolute error by expected value then we get a new value which is known as relative error.
First, calculate the absolute error. Absolute error is equal to 16 minus 15.5 which is equal to 0.5 cm.
Now the relative error will be equal to 
$RE = \frac{{0.5}}{{16}} = 0.03125$
Commonly Asked Questions
Q: Why is relative error often more useful than absolute error?
A:
Relative error is often more useful because it provides context. For example, an absolute error of 1 cm might be significant when measuring a pencil but negligible when measuring the distance between cities. Relative error accounts for the scale of the measurement.
Q: What does it mean if the relative error is 0%?
A:
A relative error of 0% means that the measured or approximated value is exactly equal to the actual value. In other words, there is no error in the measurement or approximation.
Q: Can relative error exceed 100%?
A:
Yes, relative error can exceed 100%. This happens when the absolute error is larger than the actual value itself, indicating a very significant error in measurement or approximation.
Q: How does the concept of error propagation relate to absolute and relative errors?
A:
Error propagation refers to how errors in individual measurements combine when those measurements are used in calculations. Understanding absolute and relative errors is crucial for accurately estimating how errors will propagate through complex calculations.
Q: How do rounding errors contribute to absolute and relative errors?
A:
Rounding errors occur when we simplify numbers by reducing the number of decimal places. These can contribute to both absolute and relative errors by introducing small discrepancies between the rounded value and the true value.
Frequently Asked Questions (FAQs)
Q: Can you explain how absolute and relative errors relate to the concept of least count in measurements?
A:
The least count of an instrument is the smallest measurement it can reliably make, which often corresponds to the smallest division on its scale. This least count effectively sets a lower limit on the absolute error of any measurement made with that instrument. The relative error will then depend on the magnitude of the measurement relative to this least count.
Q: How do absolute and relative errors relate to the concept of margin of error in polling and surveys?
A:
The margin of error in polling is typically expressed as a percentage, which is a form of relative error. For example, a poll might report that 52% of respondents favor a candidate, with a margin of error of ±3%. This means the true percentage is likely between 49% and 55%. The absolute error here would be ±3 percentage points, but expressing it as a relative error (about ±5.8% relative to 52%) would be less informative in this context.
Q: Can you explain how absolute and relative errors might be used in financial forecasting?
A:
In financial forecasting, both absolute and relative errors are important. Absolute errors give a concrete idea of how far off predictions might be in currency terms, which is crucial for budgeting. Relative errors, often expressed as percentages, provide context for how significant these deviations are relative to the overall figures, which is important for assessing the reliability of the forecast.
Q: How do absolute and relative errors relate to the concept of significant digits in scientific notation?
A:
The number of significant digits used to express a measurement implies a certain level of absolute error. For example, 1.00 × 10³ implies an absolute error of about ±5 in the last digit, or ±0.005 × 10³. The relative error can then be calculated from this implied absolute error, which in this case would be about 0.5%.
Q: How might the concepts of absolute and relative error be applied in everyday life?
A:
These concepts apply in many everyday situations. For example, when budgeting, a $10 error (absolute) in a $100 purchase is more significant (10% relative error) than in a $1000 purchase (1% relative error). In cooking, a 1-minute error (absolute) is more significant when boiling an egg (relative error of about 10% for a 10-minute boil) than when slow-cooking a roast (relative error of about 0.1% for a 16-hour cook).
Q: How do absolute and relative errors factor into the reporting of scientific results?
A:
In scientific reporting, measurements are typically reported with their associated errors. For example, a length might be reported as 10.2 ± 0.1 cm (absolute error) or 10.2 cm ± 1% (relative error). This allows other scientists to assess the reliability of the results and use them appropriately in further analysis or experiments.
Q: Can you explain how absolute and relative errors might be used in quality control processes?
A:
In quality control, acceptable ranges for measurements are often specified. These can be expressed as absolute errors (e.g., ±0.1 mm) or relative errors (e.g., ±2%). Items falling outside these ranges would be considered defective. The choice between absolute and relative error often depends on whether the acceptable variation scales with the size of the item or is constant across all sizes.
Q: How do absolute and relative errors relate to the concepts of accuracy and precision in scientific measurements?
A:
Accuracy relates to how close a measurement is to the true value, which is directly measured by absolute and relative errors. Precision, on the other hand, relates to the consistency or reproducibility of measurements. A set of measurements can be precise (consistent) but inaccurate (far from the true value), or accurate on average but imprecise.
Q: Why is it important to consider both absolute and relative errors when choosing measuring instruments?
A:
Considering both types of errors helps in selecting an instrument appropriate for the task. An instrument with a small absolute error might still have a large relative error for small measurements. Conversely, an instrument with a small relative error for large measurements might have an unacceptably large absolute error for smaller measurements.
Q: How do absolute and relative errors come into play when combining measurements in calculations?
A:
When combining measurements in calculations, errors can propagate and compound. Absolute errors are typically added or subtracted directly when adding or subtracting measurements. For multiplication and division, relative errors are often more useful as they can be added as percentages.
Articles
News and Notifications
Latest updates
Classroom Precautions During Covid-19
Aug 18, 2025
What is Mental Health For Students
Aug 18, 2025