Area Of A Quarter Circle

Area of a Quarter Circle

Edited By Team Careers360 | Updated on Jul 02, 2025 05:11 PM IST

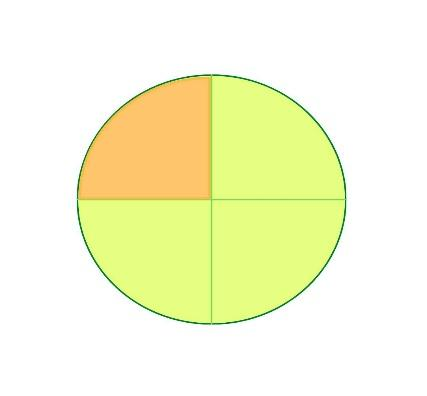
The circle is a shape with zero corners. It is symmetrical over any of its diameters. It gets divided into symmetrical parts when divided along the diameter. The symmetrical parts have equal areas. You must have noticed the way pizza is cut. Generally, pizza comes in a circular shape which is then further divided into 4,6, or 8 pieces. And all the pieces are of equal area. When a circle is divided along its diameter into four equal parts, we get 4 quarter circles. As the four parts have equal area, the area of a quarter circle is \frac{1}{4}^{th} that of the circle.

This Story also Contains

How Much is a Quarter?
A Quarter of Different Numbers
What is an Area of a Quarter Circle?
What is the Circumference of a Quarter Circle?
Examples

How Much is a Quarter?

A quarter meaning in maths is \frac{1}{4}. A quarter of any quantity is \frac{1}{4}^{th} of the whole quantity. So when you are talking about a quarter circle, it is \frac{1}{4}^{th} of the circle i.e. one-fourth of a circle.

1706336987621

A Quarter of Different Numbers

To find the quarter of any number, we divide the number by 4.

Quarter of 100

A quarter of 100 means, we need to find the value of \frac{1}{4}^{th} of 100. For this, we need to divide the 100 by 4.

A quarter of 100 = \frac{1}{4}*100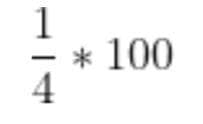 1706336988109

A quarter of 100 = 25

Quarter of 500

We need to find \frac{1}{4}^{th} of 500.

A quarter of 500 = \frac{1}{4}*500

A quarter of 500 = 125

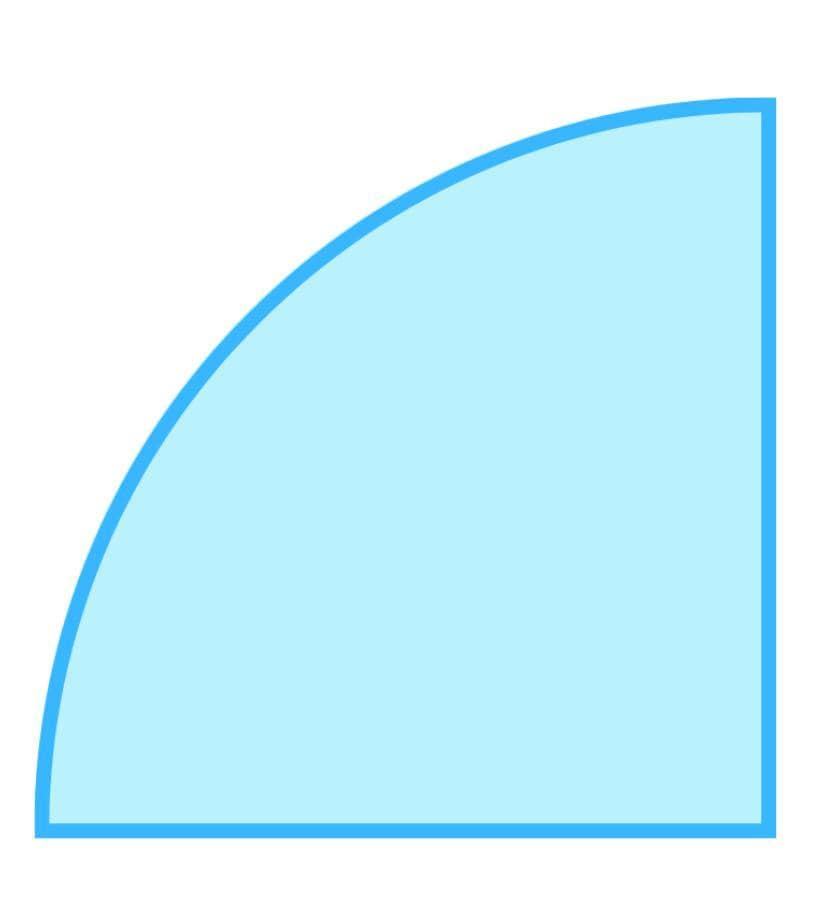
What is an Area of a Quarter Circle?

The area of any is the amount of a plane enclosed by it. In the context of 2D figures, it is the play bounded by the boundary of the shape. When you're talking about 3D figures, surface area forms the boundary of the shape.

The area of a circle is given by the formula \pi r^{2}. Here 'r' is the radius of the circle.

Area of a quarter circle =\frac{1}{4} Area of a circle

=\frac{1}{4} \pi r^{2}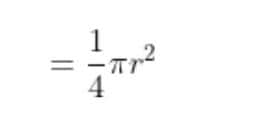 1706336988051 1706336988360

What is the Circumference of a Quarter Circle?

The circumference of a circle is the curve length or perimeter of the circle. When we find the circumference we get the value of the border of the circle. When a circle is divided into 4 equal parts, its circumference gets divided into four parts too.

Circumference of the circle is given by the formula 2\pi r. Here, 'r' stands for the radius of the circle.

Circumference of a quarter circle = \frac{1}{4} circumference of a circle

=\frac{1}{4}*2\pi r

=\frac{1}{2}*\pi r

The circumference of a quarter circle is \frac{1}{2}*\pi r

Examples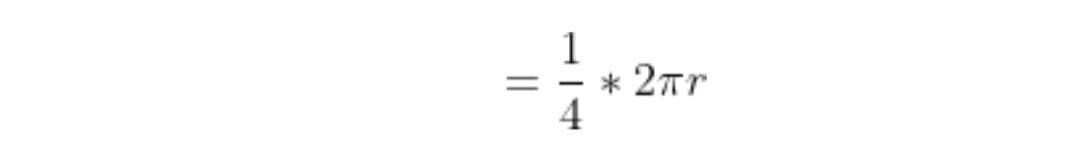

What is the value of a quarter to 2?

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Quarter to 2 means, we need to find \frac{1}{4}^{th} of the number 2.

Quarter to 2 = \frac{1}{4}*2

= \frac{1}{2}

What is the area of a quarter of a circle having a radius of 8 cm?

The area of a quarter circle formula is \frac{1}{4} \pi r^{2}.

Area =\frac{1}{4} \pi r^{2}\\

Area =\frac{1}{4} \pi (8)^{2}\\

Area =\frac{1}{4} \pi(64) \\

Area = 16\pi 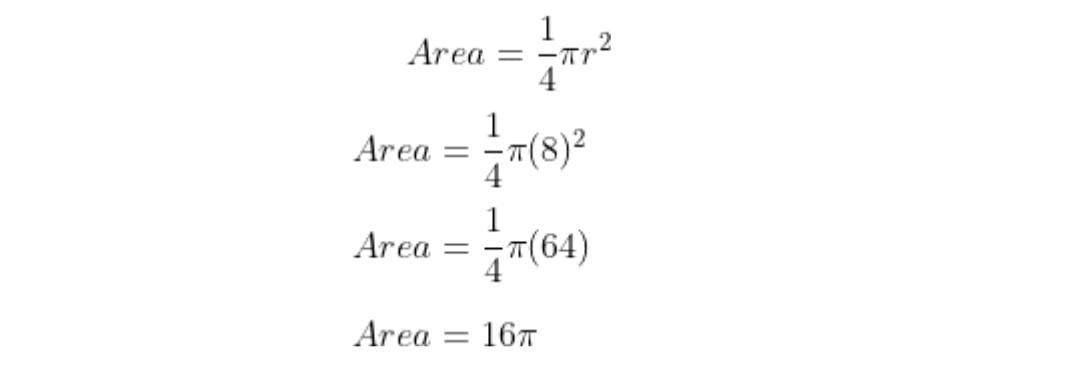1706336988199

A pizza has a total area of 76 sq.cm. It is divided into four equal parts. Find the area of each quarter.

The total area of pizza = 76 sq. cm

Area of each quarter = \frac{1}{4} * 76 \\

= 19sq. cm

The area of each pizza piece is 19 sq.cm.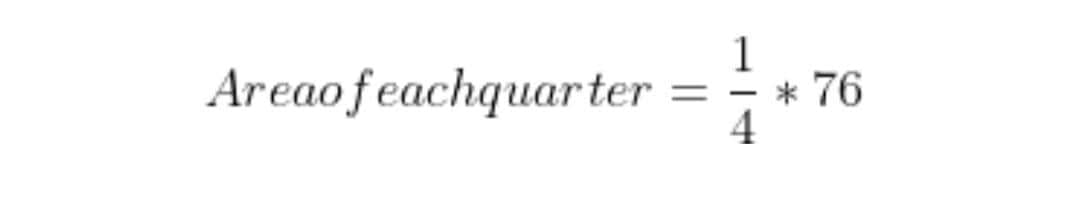 1706336987787

Find the circumference of a circle having a quarter of the circumference 20cm

The circumference of a quarter of a circle is 20cm.

Circumference of circle = 4 * 20

= 80cm

What is the value of the area of a quarter circle whose circumference is \pi ?

The formula for the circumference of a quarter circle is \frac{1}{2}\pi r \\

Circumference = \frac{1}{2}\pi r \\

\pi = \frac{1}{2} \pi r \\

r = 2 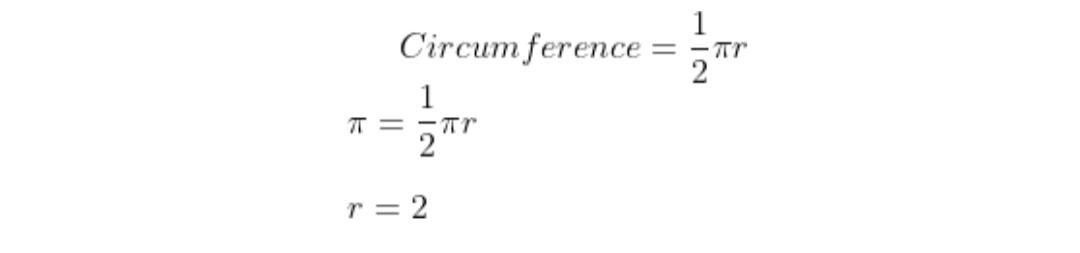1706336987706

The formula for the area of a quarter circle is \frac{1}{4} \pi r^{2}

Area = \frac{1}{4} \pi r^{2} \\

Area = \frac{1}{4} \pi (2)^{2}

Area = \frac{1}{4} \pi (4)

Area = \pi

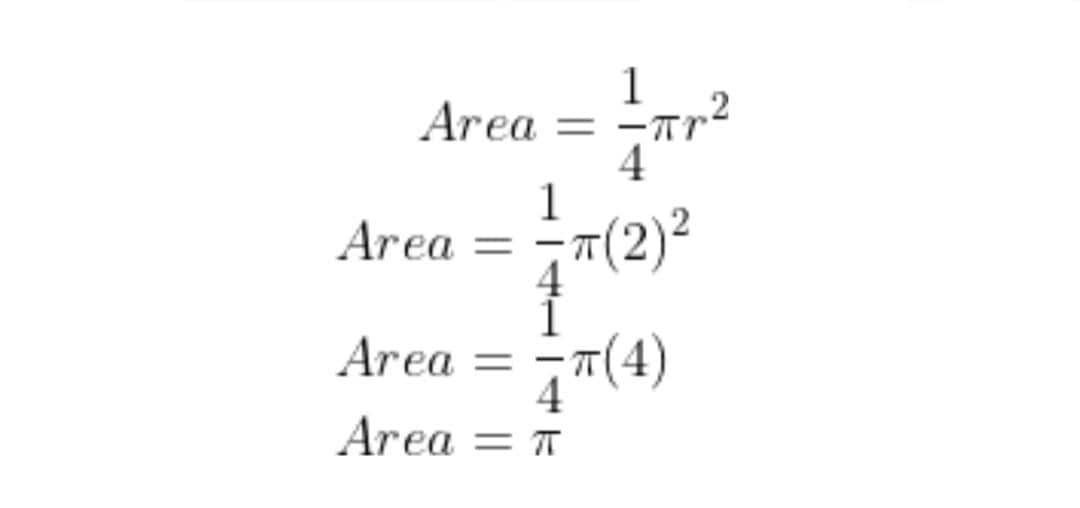
1706336988267

Frequently Asked Questions (FAQs)

1. What is the formula for the area of a quarter circle in terms of diameter?

The formula is given as \frac{1}{16}*\pi*d^{2}.

2. What is the volume of a quarter of a sphere?

The volume of the quarter sphere = \frac{1}{3} \pi r^{3}.

3. For what value of r circumference of a quarter circle and its area is equal?

When the value of r = 2, the values of the circumference and area of a quarter circle are the same.

4. What is the relation between the circumference and area of a quarter circle?

Circumference = \frac{1}{2}*\pi r

Area = \frac{1}{4} \pi r^{2}

The relation is given as follows:

Area = = \frac{1}{2}*r*circumference

5. What is the total perimeter of a quarter-shaped pizza?

The pizza along with its curved length has two straight lines. The two straight sides have the length of the radius.

Total perimeter = 2r + \frac{1}{2}\pi r

6. How does the area of a quarter circle compare to the area of a semicircle with the same radius?

The area of a quarter circle is exactly half the area of a semicircle with the same radius. This is because a semicircle is half of a full circle, while a quarter circle is one-fourth of a full circle.

7. How does the area of a quarter circle relate to the area of the sector it forms in the full circle?

The area of a quarter circle is equal to the area of a 90-degree sector in the full circle. This is because a quarter circle corresponds to a central angle of 90 degrees, which is 1/4 of the full 360 degrees of a circle.

8. How does the area of a quarter circle relate to the area of a circular segment with a 90-degree central angle?

The area of a quarter circle is equal to the area of a circular segment with a 90-degree central angle. This is because both shapes represent the same portion (one-fourth) of a full circle.

9. How is the area of a quarter circle related to the area of a full circle?

The area of a quarter circle is exactly one-fourth of the area of a full circle. This is because a quarter circle represents 1/4 of the total area of a complete circle.

10. What is the formula for calculating the area of a quarter circle?

The formula for the area of a quarter circle is A = (π * r²) / 4, where A is the area and r is the radius of the circle. This formula is derived from the full circle area formula (π * r²) divided by 4.

11. Why do we divide the full circle area formula by 4 to get the quarter circle area?

We divide the full circle area formula by 4 because a quarter circle is exactly one-fourth of a complete circle. By dividing the full area by 4, we obtain the area of one of these four equal parts.

12. How does changing the radius affect the area of a quarter circle?

The area of a quarter circle is proportional to the square of its radius. This means that if you double the radius, the area will increase by a factor of 4. If you triple the radius, the area will increase by a factor of 9, and so on.

13. Can the area of a quarter circle ever be negative?

No, the area of a quarter circle can never be negative. Area is always a positive quantity, representing the amount of space enclosed by a shape. Even if the radius is negative, we use its absolute value in calculations, resulting in a positive area.

14. Can you express the area of a quarter circle in terms of its arc length?

Yes, if L is the arc length of the quarter circle, its area can be expressed as A = L² / (2π). This is because L = (π * r) / 2 for a quarter circle, so r = 2L / π. Substituting this into the quarter circle area formula gives A = (π * (2L / π)²) / 4 = L² / (2π).

15. What is a quarter circle?

A quarter circle is one-fourth of a complete circle, formed by dividing a circle into four equal parts. It represents a 90-degree angle or a right angle at the center of the circle.

16. How can you find the radius of a quarter circle if you know its area?

To find the radius of a quarter circle given its area, use the formula r = √((4 * A) / π), where A is the given area. This is derived by solving the quarter circle area formula A = (π * r²) / 4 for r.

17. Can you express the area of a quarter circle in terms of its circumference?

Yes, you can express the area of a quarter circle in terms of its circumference. If C is the circumference of the full circle, the area of the quarter circle is A = C² / (16π). This is because C = 2πr, so r = C / (2π), and substituting this into the quarter circle area formula gives A = (π * (C / (2π))²) / 4 = C² / (16π).

18. What's the relationship between the perimeter of a quarter circle and its area?

The perimeter of a quarter circle consists of two radii and a quarter of the circle's circumference. If we call this perimeter P, then P = 2r + (πr/2). The area A is related to this perimeter by the equation A = (P² - 2r²) / (2π). This relationship is more complex than for a full circle due to the straight edges of the quarter circle.

19. How can you use the area of a quarter circle to find the area of a circular ring (annulus)?

To find the area of a circular ring (annulus), you can subtract the areas of the quarter circles formed by the inner and outer radii. If R is the outer radius and r is the inner radius, the area of the quarter annulus is A = (π * R²) / 4 - (π * r²) / 4 = (π * (R² - r²)) / 4.

20. How does the area of a quarter circle relate to the concept of moment of inertia in physics?

The area formula of a quarter circle is similar to the formula for the moment of inertia of a circular disk about its center. The moment of inertia is I = (1/2) * m * r², where m is the mass. If we consider a quarter circular disk of uniform density ρ, its mass would be m = ρ * (π * r²) / 4, and its moment of inertia about the center would be I = (1/8) * ρ * π * r⁴, showing a fourth-power relationship with radius, compared to the second-power relationship in area.

21. Can you use quarter circles to explain the concept of phase in wave motion?

Yes, quarter circles are useful in explaining phase in wave motion. A complete cycle of a wave corresponds to a full circle (2π radians or 360°). A quarter circle represents a phase difference of π/2 radians or 90°. This is often used to describe the relationship between sine and cosine waves, which are said to be "out of phase" by a quarter cycle.

22. How does the area of a quarter circle compare to the area of a square with the same side length as the radius?

The area of a quarter circle is always less than the area of a square with side length equal to the radius. The quarter circle's area is (π * r²) / 4, which is approximately 0.785 * r², while the square's area is r². The difference is about 21.5% of the square's area.

23. What's the relationship between the area of a quarter circle and the area of an equilateral triangle with the same side length as the radius?

The area of a quarter circle is larger than the area of an equilateral triangle with side length equal to the radius. The quarter circle's area is (π * r²) / 4 ≈ 0.785 * r², while the equilateral triangle's area is (√3 * r²) / 4 ≈ 0.433 * r². The quarter circle's area is about 1.81 times larger.

24. What's the difference between the area of a quarter circle and a quadrant?

There is no difference. A quadrant is another term for a quarter circle. Both refer to one-fourth of a circle and have the same area formula: A = (π * r²) / 4.

25. How does the area of a quarter circle compare to the area of an inscribed right-angled triangle?

The area of a quarter circle is always larger than the area of the inscribed right-angled triangle formed by its two radii. The triangle's area is r² / 2, while the quarter circle's area is (π * r²) / 4, which is approximately 0.285 * r² larger than the triangle's area.

26. What's the limit of the ratio of a quarter circle's area to its radius as the radius approaches infinity?

As the radius approaches infinity, the ratio of a quarter circle's area to its radius also approaches infinity. This is because the area grows quadratically with the radius (A = (π * r²) / 4), while the radius grows linearly. The limit of this ratio as r approaches infinity is: lim(r→∞) ((π * r²) / 4) / r = lim(r→∞) (π * r) / 4 = ∞.

27. Can you find the area of a quarter circle using calculus?

Yes, you can find the area of a quarter circle using calculus. Using polar coordinates, the area can be calculated as the integral of r²/2 from 0 to π/2: A = ∫(0 to π/2) (r²/2) dθ = (r²/2) * (π/2) = (π * r²) / 4, which is the same result as the standard formula.

28. How does the area of a quarter circle change if you increase its central angle beyond 90 degrees?

If you increase the central angle beyond 90 degrees, the resulting shape is no longer a quarter circle but a larger sector. The area will increase proportionally to the increase in the central angle. For example, a 120-degree sector would have an area of (π * r²) / 3, which is larger than a quarter circle's (π * r²) / 4.

29. What's the relationship between the areas of quarter circles from concentric circles?

For concentric circles, the ratio of the areas of their quarter circles is equal to the square of the ratio of their radii. If you have two concentric circles with radii r₁ and r₂, the ratio of their quarter circle areas is (A₁ / A₂) = (r₁ / r₂)². This is because each area is proportional to the square of its radius.

30. How does the area of a quarter circle compare to the area of a regular octagon inscribed in the same circle?

The area of a quarter circle is slightly larger than the area of one-half of a regular octagon inscribed in the same circle. The area of the inscribed octagon is 2√2 * r², or about 2.828 * r². Half of this is 1.414 * r², which is less than the quarter circle's area of (π * r²) / 4 ≈ 0.785 * r².

31. How does the area of a quarter circle relate to the volume of a sphere with the same radius?

The area of a quarter circle is exactly 3/8 of the surface area of a sphere with the same radius. This relationship comes from the fact that the surface area of a sphere is 4πr², while the area of a quarter circle is (πr²) / 4. The ratio between these is (πr² / 4) / (4πr²) = 1/16, which is equivalent to 3/8 when comparing to one-quarter of the sphere's surface.

32. What's the relationship between the areas of quarter circles from two circles where one radius is twice the other?

If one circle has a radius twice that of another, the area of its quarter circle will be four times larger. This is because the area of a quarter circle is proportional to the square of its radius. If r₂ = 2r₁, then A₂ = (π * (2r₁)²) / 4 = π * r₁² = 4 * ((π * r₁²) / 4) = 4A₁.

33. What's the relationship between the area of a quarter circle and the area of a circular sector with the same radius but half the central angle (45 degrees)?

The area of a quarter circle (90-degree sector) is exactly twice the area of a 45-degree sector with the same radius. This is because the area of a sector is directly proportional to its central angle. A 45-degree sector has an area of (π * r²) / 8, which is half of the quarter circle's area of (π * r²) / 4.

34. How does the concept of a quarter circle relate to radian measure?

A quarter circle corresponds to a central angle of π/2 radians, which is equivalent to 90 degrees. This relationship is fundamental in understanding how radian measure relates to familiar degree measures and circular geometry. The area formula for a quarter circle can be written as A = r² * (π/2) / 2, where π/2 is the radian measure of the central angle.

35. Can you use the area of a quarter circle to find the length of an arc that's not a quarter of the circumference?

Yes, you can use the concept of a quarter circle to find the length of any arc. If you know the central angle θ (in radians) and the radius r, the arc length is L = r * θ. This comes from the fact that a full circle (2π radians) has a circumference of 2πr, so the ratio of any arc to the full circumference is the same as the ratio of its central angle to 2π.

36. How does the area of a quarter circle relate to the concept of pi?

The area of a quarter circle directly involves pi in its formula: A = (π * r²) / 4. This relationship showcases how pi, as the ratio of a circle's circumference to its diameter, is fundamental in calculating circular areas. The quarter circle formula essentially represents one-fourth of pi multiplied by the square of the radius.

37. What's the significance of the quarter circle in trigonometry?

The quarter circle is significant in trigonometry as it represents the first quadrant of the unit circle. In this quadrant, all trigonometric functions (sine, cosine, tangent, etc.) are positive. The x and y coordinates of any point on this quarter circle directly give the cosine and sine values for the angle formed with the x-axis, which is fundamental to understanding trigonometric functions.

38. How can you use quarter circles to visualize the difference between arithmetic and geometric means?

Quarter circles can be used to visualize the difference between arithmetic and geometric means of two positive numbers a and b. If you draw a quarter circle with radius (a+b)/2 (the arithmetic mean), the length of the perpendicular from the center to the line connecting (a,0) and (0,b) is √(ab) (the geometric mean). This visually demonstrates that the geometric mean is always less than or equal to the arithmetic mean.

39. How does the area of a quarter circle relate to the concept of radians in calculus?

In calculus, the area of a quarter circle is often used to introduce the concept of radians. The formula A = (1/2) * r * (r * θ), where θ is in radians, shows that the area of a sector is half the product of the radius and arc length. For a quarter circle, θ = π/2, giving the familiar formula A = (π * r²) / 4.

40. Can you use quarter circles to explain the concept of steradian in three-dimensional geometry?

Yes, quarter circles can help explain steradians. A steradian is the three-dimensional analog of a radian. Just as a radian is defined by an arc length equal to the radius on a circle, a steradian is defined by a surface area equal to the square of the radius on a sphere. A quarter circle extended into three dimensions forms a solid angle of π/2 steradians, which is one-eighth of a full sphere (4π steradians).

41. How can quarter circles be used to understand the concept of angular velocity?

Quarter circles can help visualize angular velocity. If an object moves along the arc of a quarter circle of radius r in time t, its angular velocity ω is π/(2t) radians per second. This is because it covers an angle of π/2 radians (90 degrees) in time t. The linear velocity v at any point is related to this angular velocity by v = r * ω, which is tangent to the circle at that point.

42. How does the area of a quarter circle relate to the concept of work done in physics?

The area of a quarter circle can be related to work done in physics when dealing with rotational motion. If a constant torque τ is applied through an angle of π/2 radians (a quarter turn), the work done is W = τ * (π/2). This is analogous to the area of a quarter circle, where the torque plays a role similar to the radius, and the angle turned is like the central angle of the sector.

43. How can quarter circles help in understanding the concept of solid angle in three-dimensional geometry?

Quarter circles can help understand solid angles. A solid angle is measured in steradians and represents a three-dimensional angle. The solid angle subtended by a quarter circle extended into a three-dimensional cone is π/2 steradians. This is one-eighth of the total solid angle around a point (4π steradians), just as a quarter circle is one-fourth of the total angle around a point in two dimensions