Absolute Value: Definition, Equation and Properties with Examples
The separation of a number from a number line's origin is referred to as a number's absolute value. It is denoted by the symbol |a|, which specifies the size of any integer 'a'. Any integer's absolute value, regardless of its sign or whether it is positive or negative, will be a non-negative real number. To write the modulus of a, two vertical lines |a| are used to symbolize it.
This Story also Contains
- What Is A Number's Absolute Value?
- Symbol For Absolute Value
- Absolute Value in Equations or Inequalities.
- Examples For Absolute Value Of A Number
- Absolute Value Function
- Properties
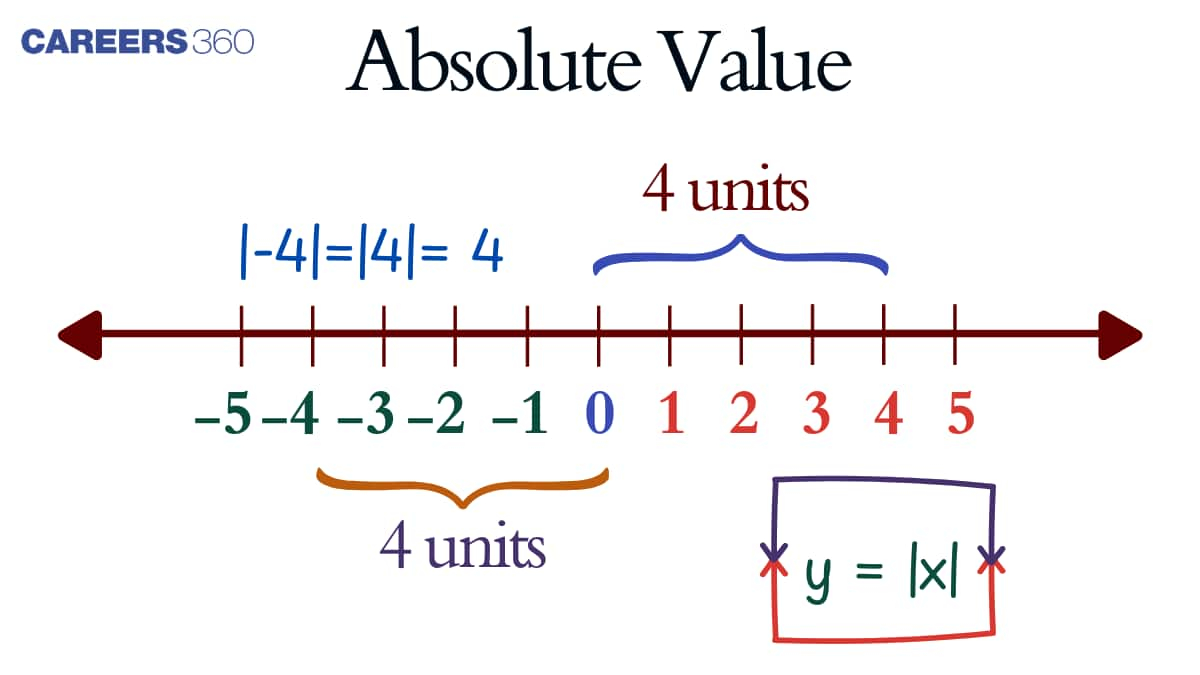
What Is A Number's Absolute Value?
The absolute value of an integer or number is how far it is from zero on a number line. Because of this, the absolute value is always positive or zero and never negative. The following definition applies to the absolute values:
|a| = ( a if a ≥ 0 )
( -a if a < 0 )
Only positive numbers will be generated if the number is positive. Additionally, the number's modulus will also be negative if it is negative. It is represented by the symbol |n|, where n is an integer.
Symbol For Absolute Value
The absolute value sign is represented by the modulus symbol "| |" and the numbers inside the symbol. For example |9| is used to represent the absolute value of nine.
Any number's absolute value is determined by how far it is from the line's origin. Additionally, it indicates whether a number is positive or negative and its polarity. It can never be negative since it represents distance, which cannot be negative. It is therefore always positive.
‘| |’ – Absolute value symbols, ‘| | pipes’ are used to represent the absolute values.
The number "a'' is the one whose absolute value needs to be determined, for example: "|a|".
Absolute Value in Equations or Inequalities.
The symbol |a| is used to signify a number's absolute value. On a number line, this value or number signifies the separation (absolute difference) between a and 0. An absolute value equation is one that contains an absolute value expression. Absolute value inequalities come in two different varieties. One with |a| < b or less, and the other with |a|> b or more.
Examples For Absolute Value Of A Number
Let's look at a few illustrations of the absolute value of numbers.
|-1| = 1
|-14| = 14
|1| = 1
|0| = 0
|7| = 7
Absolute Value Function
If f(x) = |x|, the absolute value function is defined as follows:
f(x) = +x if x > 0,
And, f(x) = -x if x < 0
Properties
If x and y are real numbers, and the absolute values meet the criteria listed below:
Property | Expression |
Non-negativity | | x |≥ 0. |
Positive-definiteness | |x| = 0 => x = 0. |
Multiplicatively | | x × y| = |x| × |y|. |
Subadditivity | |x + y| ≤ |x| + y|. |
Symmetry | |-x| =|x| |
Identity of indiscernible (equivalent to positive definiteness) | |x – y| = 0 ↔ x = y |
Triangle inequality | |x – y| ≤ | x – z | + |z – x| |
Preservation of division (equivalent to multiplicatively) | |x / y| = | x | / | y| |
Equivalent to subadditivity | |x – y| ≥| | x |–| y | | |
Frequently Asked Questions (FAQs)
Any integer's absolute value is always positive and never negative.
The absolute value of -7 is 7. Its sign is |-7|, which equals 7.
In absolute terms, -12 equals 12. Given that there are 12 spaces between -12 and 0 on a number line.
Absolute value is denoted by the symbol |x|, where x is an integer.
|4| = 4 is the absolute value of four.
The distance a number is from zero on a number line is represented by its absolute value.