Acute Angle : Definition, Formula, Degrees, Images, Applications and Examples

We define acute angle as an angle which measures less than $90^{\circ}$. When the clock strikes $4: 30$, the angle made by the hands is an example of acute angle. Angles such as $33^\circ$, $65^\circ$ degree are all examples of acute angles. Numerous figures like triangle, parallelogram, trapezoid, etc. have at least one acute angle. Hence we can say that it is very commonly found around us in various shapes and forms. Acute angles are an integral part of architecture, construction and physics when defining motion and projectiles.

This Story also Contains

1. What is an Acute Angle?
2. What is Acute Angle Triangle?
3. Acute Angle Degree
4. Acute Angle Examples from daily life
5. Acute Angle Examples

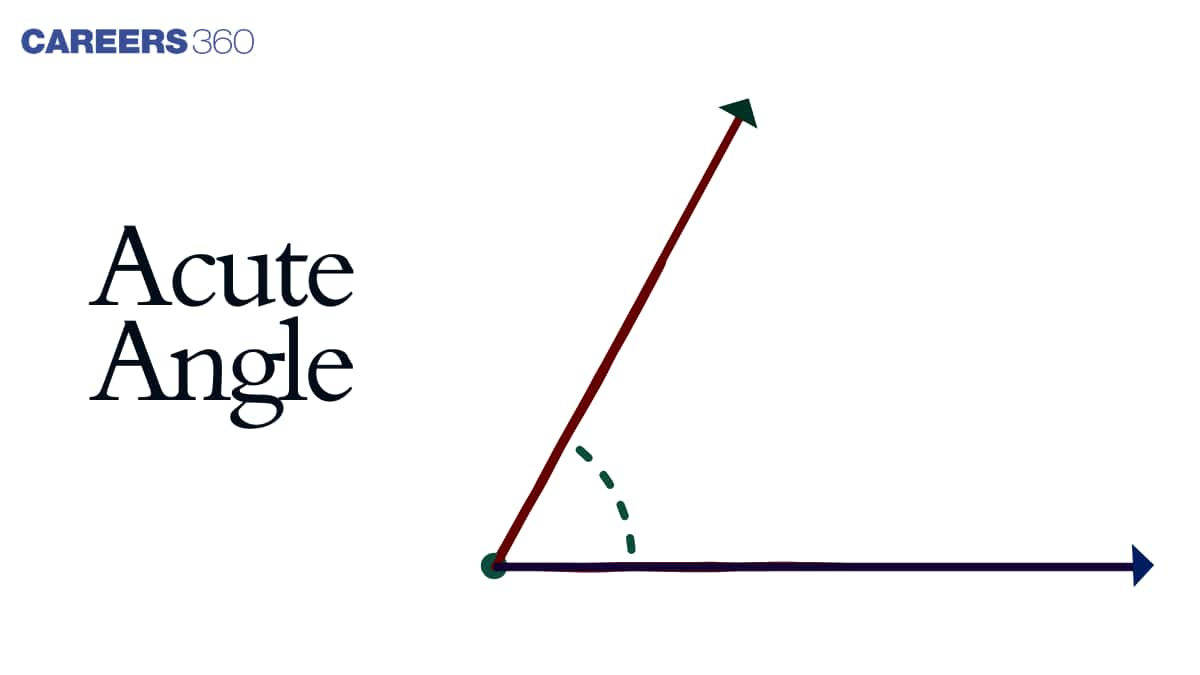
In this article we will learn about the definition of acute angle, acute angle meaning, what is acute angle triangle and much more.

What is an Acute Angle?

If we go by the definition of acute angle, we can say that when the angle formed when 2 rays meet at a vertex measures less than $90^{\circ}$, then it is termed as an acute angle. It means that its measure should always be less than 90 degrees and this condition has to be always fulfilled to classify an angle as acute angle.

Acute Angle Definition

We can say that an acute angle is defined as an angle that always measures in the range of $0^{\circ}$ to $90^{\circ}$. Few examples of acute angles are $60^{\circ}, 30^{\circ}, 45^{\circ}$ etc.

Acute angle Images

The below diagrams shows the acute angle images measuring $30^{\circ}$ and $20^{\circ}$

What is Acute Angle Triangle?

When all the internal angles are less than 90 degrees, then it is an acute angle triangle. For example ,consider triangle XYZ below :

Acute Angle Degree

Examples of acute angle degrees are $64^{\circ}, 32^{\circ}, 40^{\circ}, 69^{\circ}, 80^{\circ}, 22^{\circ}$.

Acute Angle Examples from daily life

Some real-life examples of acute angles:

• A pair of open scissors.
• Slices of pizza.
• Hands of a clock.

Acute Angle Examples

Following are few more examples of acute angle:

Example 1: Choose the angles which can be classified as acute angles.

Solution:

Option a) $50^{\circ}$ is less than $90^{\circ}$. Therefore, it is an acute angle.
Option b) $107^{\circ}$ is more than $90^{\circ}$. Therefore, it is not an acute angle, it is an obtuse angle.
Option c) $101^{\circ}$ is more than $90^{\circ}$. Therefore, it is not an acute angle, it is an obtuse angle.
Option d) $20^{\circ}$ is less than $90^{\circ}$. Therefore, it is an acute angle.

Example 2: Observe the clocks shown below carefully and identify the times at which the hands form an acute angle.

Solution:

We can observe that at 10 o'clock and 11 o'clock, the hour hand and the minute hand form an acute angle.

Therefore, an acute angle is formed by the clocks at 10 o'clock and 11 o'clock.

Example 3: Is the following triangle acute?

Solution:

All the 3 angles inside an acute triangle should measure less than $90^{\circ}$. From the figure, we can see that two angles measure $45^{\circ}$ each and $\angle \mathrm{Y}$ is $90^{\circ}$. Hence, this is not an acute triangle, but a right-angled triangle.

Example 4: Find y in the given triangle and state whether it is an acute angle triangle.

Solution:

As we know,
The sum of the interior angles in a triangle is $180^{\circ}$,
Thus,
In $\triangle \mathrm{PQR}$,

$
\begin{aligned}
& 70^{\circ}+\angle \mathrm{R}+60^{\circ}=180^{\circ} \\
& \angle \mathrm{R}=180^{\circ}-\left(60^{\circ}+70^{\circ}\right) \\
& \angle \mathrm{R}=\left(\mathrm{y}^{\circ}\right)=50^{\circ}
\end{aligned}
$

$
\angle \mathrm{P}+\angle \mathrm{Q}+\angle \mathrm{R}=180^{\circ} \text {, (angle sum property of triangle). }
$

Since all three angles $\angle \mathrm{P}, \angle \mathrm{Q}, \angle \mathrm{R}$ measure less than $90^{\circ}, \triangle \mathrm{PQR}$ is an acute angle triangle

Example 5: Identify the acute angles in the given polygon PQRST.

Solution:

Sum of the interior angles of a pentagon $=540^{\circ}$
Now,

$
\begin{aligned}
& \angle \mathrm{P}+\angle \mathrm{Q}+\angle \mathrm{R}+\angle \mathrm{S}+\angle \mathrm{T}=540^{\circ} \\
& 80^{\circ}+150^{\circ}+\angle \mathrm{R}+95^{\circ}+138^{\circ}=540^{\circ} \\
& \angle \mathrm{R}=540^{\circ}-463^{\circ} \\
& \angle \mathrm{R}=\left(\mathrm{x}^{\circ}\right)=77^{\circ}
\end{aligned}
$

Thus, $\angle \mathrm{P}$ and $\angle \mathrm{R}$ measure less than $90^{\circ}$ and are acute angles.

List of Topics Related to Acute Angle