Additive Inverse (Definition, Properties & Examples)
Every number has a unique counterpart that cancels its value when added to it. This counterpart is known as the additive inverse. The concept of additive inverse is a fundamental topic in arithmetic, algebra, integers, rational numbers, and number systems. It helps simplify equations, understand mathematics related operations, and solve algebraic expressions efficiently. Questions related to additive inverses are frequently asked in school mathematics, competitive examinations, and quantitative aptitude tests. In this article, we will discuss the meaning of additive inverse, its definition, properties, formulas, examples, applications, and solved questions.
This Story also Contains
- What is Additive Inverse?
- Additive Inverse Formula
- Properties of Additive Inverse
- Additive Inverse in Different Number Systems
- How to Find the Additive Inverse?
- Difference Between Additive Inverse and Multiplicative Inverse
- Best Books for Additive Inverse
- Shortcut Tips and Tricks for Additive Inverse
- Important Formula Table
- Practice Questions based on Additive Inverse
- List of Topics related to Additive Inverse
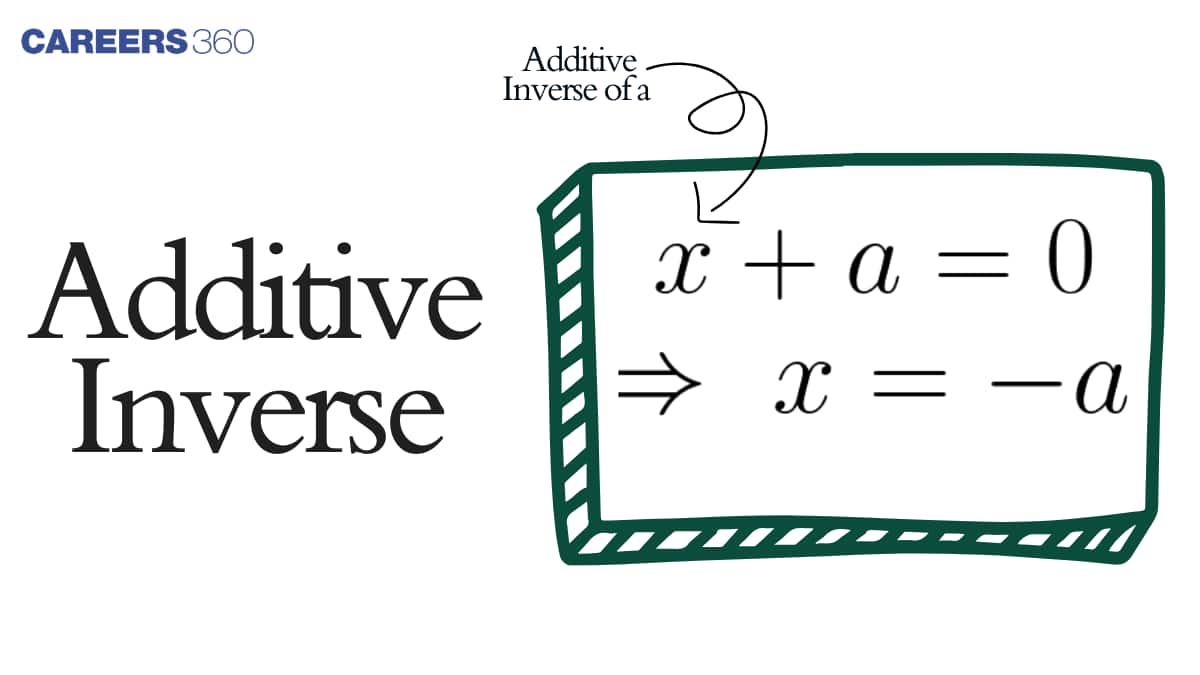
What is Additive Inverse?
The additive inverse is one of the most fundamental concepts in mathematics and number systems. It refers to a number that, when added to a given number, results in zero. Additive inverses are widely used in arithmetic, algebra, integers, rational numbers, real numbers, vectors, and higher mathematics. Understanding additive inverse helps students simplify equations, solve algebraic expressions, and perform mathematical operations accurately.
Additive Inverse Meaning in Simple Words
In simple words, the additive inverse of a number is the same number with the opposite sign.
For example:
The additive inverse of $5$ is $-5$.
The additive inverse of $-8$ is $8$.
The additive inverse of $\frac{3}{4}$ is $-\frac{3}{4}$.
When a number and its additive inverse are added together, the result is always zero.
Example:
$7+(-7)=0$
Definition of Additive Inverse
The additive inverse of a number is the number that produces zero when added to the original number.
Mathematically,
If $a$ is a number, then its additive inverse is: $\boxed{-a}$ because $a+(-a)=0$
This definition applies to integers, fractions, decimals, real numbers, and complex numbers.
Real-Life Examples of Additive Inverse
Additive inverses are used in many everyday situations involving gains and losses, increases and decreases, or opposite quantities.
| Situation | Additive Inverse Concept |
|---|---|
| Depositing ₹500 and withdrawing ₹500 | $500$ and $-500$ |
| Temperature rise and fall | $+10^\circ C$ and $-10^\circ C$ |
| Elevator moving up and down | Positive and negative displacement |
| Profit and loss | Equal profit and loss cancel each other |
| Credit and debit transactions | Opposite financial operations |
Example
If a bank account receives ₹1000 and later ₹1000 is withdrawn:
$1000+(-1000)=0$
The net change is zero.
Why Additive Inverse is Important in Mathematics
The concept of additive inverse forms the foundation of algebra and number systems.
Importance of Additive Inverse
Helps solve linear equations.
Simplifies algebraic expressions.
Essential for integer arithmetic.
Used in vector operations.
Important in coordinate geometry.
Helps understand positive and negative numbers.
Forms the basis of inverse operations.
Competitive Exam Relevance
Questions related to additive inverse frequently appear in:
Additive Inverse Formula
The additive inverse formula provides a simple method for finding the additive inverse of any number.
Standard Formula of Additive Inverse
If a number is represented by $a$, then its additive inverse is:
$\boxed{-a}$
The sum of a number and its additive inverse is always zero.
$\boxed{a+(-a)=0}$
Example
For:
$a=12$
Additive inverse:
$-12$
Verification:
$12+(-12)=0$
Additive Inverse of Positive Numbers
The additive inverse of a positive number is the corresponding negative number.
Examples
| Number | Additive Inverse |
|---|---|
| $5$ | $-5$ |
| $12$ | $-12$ |
| $100$ | $-100$ |
Example
$25+(-25)=0$
Therefore, the additive inverse of $25$ is:
$\boxed{-25}$
Additive Inverse of Negative Numbers
The additive inverse of a negative number is the corresponding positive number.
Examples
| Number | Additive Inverse |
|---|---|
| $-7$ | $7$ |
| $-15$ | $15$ |
| $-50$ | $50$ |
Example
$-18+18=0$
Therefore, the additive inverse of $-18$ is:
$\boxed{18}$
Additive Inverse of Zero
Zero is a special number because it is its own additive inverse.
Example
$0+0=0$
Therefore,
$\boxed{\text{Additive Inverse of }0=0}$
Properties of Additive Inverse
The additive inverse follows several important mathematical properties that are used throughout algebra and number systems.
Sum Property
The sum of a number and its additive inverse is always zero.
Mathematically,
$\boxed{a+(-a)=0}$
Example
$9+(-9)=0$
This is the most important property of additive inverses.
Uniqueness Property
Every number has exactly one additive inverse.
Example
The additive inverse of $6$ is only:
$-6$
No other number can satisfy:
$6+x=0$
Thus, additive inverses are unique.
Additive Identity Relationship
The additive inverse is closely related to the additive identity.
The additive identity is:
$\boxed{0}$
because:
$a+0=a$
The additive inverse helps produce the additive identity.
Example
$13+(-13)=0$
Closure Property
The set remains closed under addition involving additive inverses.
Example
For integers:
$8+(-8)=0$
Since 0 is also an integer, closure is maintained.
Similarly, rational numbers and real numbers are also closed under additive inverse operations.
Additive Inverse in Different Number Systems
The concept of additive inverse applies to various types of numbers.
Additive Inverse of Integers
For integers, simply change the sign.
Examples
| Integer | Additive Inverse |
|---|---|
| $10$ | $-10$ |
| $-4$ | $4$ |
| $0$ | $0$ |
Additive Inverse of Rational Numbers
For fractions, change the sign of the fraction.
Examples
| Rational Number | Additive Inverse |
|---|---|
| $\frac{3}{5}$ | $-\frac{3}{5}$ |
| $-\frac{7}{8}$ | $\frac{7}{8}$ |
Example
$\frac{3}{5}+\left(-\frac{3}{5}\right)=0$
Additive Inverse of Real Numbers
Every real number has an additive inverse.
Examples
| Real Number | Additive Inverse |
|---|---|
| $3.5$ | $-3.5$ |
| $\sqrt{2}$ | $-\sqrt{2}$ |
| $\pi$ | $-\pi$ |
Additive Inverse of Complex Numbers
For a complex number:
$a+bi$
the additive inverse is:
$\boxed{-a-bi}$
Example
Additive inverse of:
$3+4i$
is:
$-3-4i$
Verification:
$(3+4i)+(-3-4i)=0$
How to Find the Additive Inverse?
Finding the additive inverse is straightforward and requires only changing the sign of the given number.
Step-by-Step Method
Step 1
Identify the given number.
Step 2
Change its sign.
Step 3
Verify that the sum equals zero.
Example
Given:
$14$
Change sign:
$-14$
Verification:
$14+(-14)=0$
Therefore, the additive inverse is:
$\boxed{-14}$
Examples of Finding Additive Inverse
| Number | Additive Inverse |
|---|---|
| $8$ | $-8$ |
| $-12$ | $12$ |
| $\frac{5}{9}$ | $-\frac{5}{9}$ |
| $2.75$ | $-2.75$ |
| $0$ | $0$ |
Shortcut Tricks
These quick tricks can help solve additive inverse questions faster.
| Trick | Explanation |
|---|---|
| Change the sign | Positive ↔ Negative |
| Magnitude remains same | Only sign changes |
| Zero remains zero | Special case |
| Fraction rule | Change sign of fraction |
| Decimal rule | Change sign of decimal |
Common Mistakes to Avoid
Students often make simple mistakes while finding additive inverses.
Common Errors
Confusing additive inverse with reciprocal.
Changing magnitude instead of sign.
Writing $0$ as having no additive inverse.
Forgetting to change the sign of an entire algebraic expression.
Confusing additive inverse with multiplicative inverse.
Difference Between Additive Inverse and Multiplicative Inverse
Although both are inverse concepts, they serve different purposes in mathematics.
Additive Inverse vs Reciprocal
The additive inverse makes the sum equal to zero, while the multiplicative inverse (reciprocal) makes the product equal to one.
Example
For the number $5$:
Additive inverse:
$-5$
Multiplicative inverse:
$\frac{1}{5}$
Key Differences
Additive inverse is used in addition.
Multiplicative inverse is used in multiplication.
Additive inverse results in zero.
Multiplicative inverse results in one.
Comparison Table
| Feature | Additive Inverse | Multiplicative Inverse |
|---|---|---|
| Formula | $-a$ | $\frac{1}{a}$ |
| Result | $a+(-a)=0$ | $a\times\frac{1}{a}=1$ |
| Also Called | Opposite Number | Reciprocal |
| Exists for Zero? | Yes | No |
| Operation Used | Addition | Multiplication |
| Example for 8 | $-8$ | $\frac{1}{8}$ |
Understanding the additive inverse and its properties is essential for mastering number systems, algebra, integers, rational numbers, real numbers, and higher mathematical concepts.
Best Books for Additive Inverse
A clear understanding of additive inverse is essential for mastering integers, rational numbers, algebra, and number systems. These books provide strong conceptual foundations and practice exercises.
| Book Name | Best For | Why It Helps |
|---|---|---|
| NCERT Mathematics | School Mathematics | Fundamental understanding of integers and number systems |
| R.D. Sharma Mathematics | School & Competitive Exams | Detailed explanations and examples |
| Quantitative Aptitude – R.S. Aggarwal | Aptitude Exams | Covers number system concepts thoroughly |
| Fast Track Objective Arithmetic – Rajesh Verma | Competitive Exams | Useful for quick revision |
| Objective Mathematics – Arihant | Entrance Exams | Practice-oriented approach |
Shortcut Tips and Tricks for Additive Inverse
Additive inverse questions are generally straightforward, but remembering a few quick rules can help avoid mistakes during examinations.
| Trick | Explanation |
|---|---|
| Change only the sign | Positive becomes negative and vice versa |
| Magnitude remains unchanged | Only the sign changes |
| Zero is its own additive inverse | $0+0=0$ |
| Sum should always be zero | Verify your answer quickly |
| Fractions follow the same rule | $\frac{a}{b}\rightarrow-\frac{a}{b}$ |
| Decimals also follow the same rule | $2.5\rightarrow-2.5$ |
| Additive inverse is not reciprocal | Common examination mistake |
Important Formula Table
The following formulas and properties are frequently used while studying additive inverses in mathematics.
| Concept | Formula |
|---|---|
| Additive Inverse of $a$ | $-a$ |
| Basic Property | $a+(-a)=0$ |
| Additive Inverse of Fraction | $-\frac{a}{b}$ |
| Additive Inverse of Decimal | $-x$ |
| Additive Inverse of Zero | $0$ |
| Additive Inverse of Complex Number | $-(a+bi)=-a-bi$ |
Practice Questions based on Additive Inverse
Example 1: What is the additive inverse of $\frac{5}{3}$?
Solution:
Given number:
$\frac{5}{3}$
We know that the additive inverse of a number is the number which, when added to the original number, gives zero.
Therefore,
$\frac{5}{3}+\left(-\frac{5}{3}\right)=0$
Hence, the additive inverse of $\frac{5}{3}$ is:
$\boxed{-\frac{5}{3}}$
Example 2: What is the additive inverse of $-\frac{4}{9}$?
Solution:
Given number:
$-\frac{4}{9}$
The additive inverse is obtained by changing the sign of the given number.
Therefore,
$-\frac{4}{9}+\frac{4}{9}=0$
Hence, the additive inverse of $-\frac{4}{9}$ is:
$\boxed{\frac{4}{9}}$
Example 3: What is the additive inverse of $-\frac{6}{20}$?
Solution:
Let the additive inverse be $z$.
Then,
$-\frac{6}{20}+z=0$
Adding $\frac{6}{20}$ to both sides,
$z=\frac{6}{20}$
Simplifying,
$z=\frac{3}{10}$
Hence, the additive inverse of $-\frac{6}{20}$ is:
$\boxed{\frac{3}{10}}$
Example 4: What is the additive inverse of the expression $12x+45y-9z$?
Solution:
The additive inverse of an algebraic expression is obtained by multiplying the entire expression by $-1$.
Therefore,
$-1(12x+45y-9z)$
$=-12x-45y+9z$
Hence, the additive inverse of $12x+45y-9z$ is:
$\boxed{-12x-45y+9z}$
Example 5: Find the additive inverse of the fraction $\frac{-61}{-51}$.
Solution:
First simplify the given fraction:
$\frac{-61}{-51}=\frac{61}{51}$
The additive inverse is obtained by changing the sign.
Therefore,
$\frac{61}{51}+\left(-\frac{61}{51}\right)=0$
Hence, the additive inverse of $\frac{-61}{-51}$ is:
$\boxed{-\frac{61}{51}}$
Example 6: What is the additive inverse of $15$?
Solution:
Given number:
$15$
The additive inverse of a positive number is the same number with a negative sign.
Therefore,
$15+(-15)=0$
Hence, the additive inverse of $15$ is:
$\boxed{-15}$
Example 7: What is the additive inverse of $-28$?
Solution:
Given number:
$-28$
Changing the sign,
$-28+28=0$
Hence, the additive inverse of $-28$ is:
$\boxed{28}$
Example 8: What is the additive inverse of $0$?
Solution:
Zero is a special number.
Since,
$0+0=0$
the additive inverse of zero is zero itself.
Hence,
$\boxed{0}$
Example 9: Find the additive inverse of $3a-7b+2c$.
Solution:
Multiply the entire expression by $-1$.
$-1(3a-7b+2c)$
$=-3a+7b-2c$
Hence, the additive inverse of $3a-7b+2c$ is:
$\boxed{-3a+7b-2c}$
Example 10: What is the additive inverse of $4.75$?
Solution:
Given number:
$4.75$
Changing the sign,
$4.75+(-4.75)=0$
Hence, the additive inverse of $4.75$ is:
$\boxed{-4.75}$
List of Topics related to Additive Inverse
To build a stronger understanding of additive inverse and number operations, it is helpful to study related algebra and arithmetic concepts. The following topics cover important mathematical operations, algebraic identities, integers, and expressions that are closely connected to additive inverses and form the foundation of higher mathematics.
Frequently Asked Questions (FAQs)
An additive inverse of a number is simply a value that when we add to that number gives us 0.
The additive inverse of 0 is 0.
The additive inverse of -6/-5 is -6/5.
The additive inverse of -5 is 5.
No.
- Additive inverse of $a$ is $-a$.
- Reciprocal of $a$ is $\frac{1}{a}$.
