Alternate Interior Angles - Definition, Theorems, Examples

When 2 parallel lines are cut by a transversal, alternate angles are the angles formed on the opposite sides of the transversal. In other words, when two parallel lines are intersected by a transversal, in total eight angles are formed and from among these, the angles that lie on the inner side of the parallel lines and on the opposite sides of the transversal are known as the alternate interior angles. In this article we are going to discuss about what are alternate interior angles, alternate exterior angles, co interior angles and much more along with their examples.

This Story also Contains

1. What are alternate Interior Angles?
2. Converse of the Alternate Interior Angles Theorem
3. Co-interior Angles
4. Alternate Interior Angles Examples

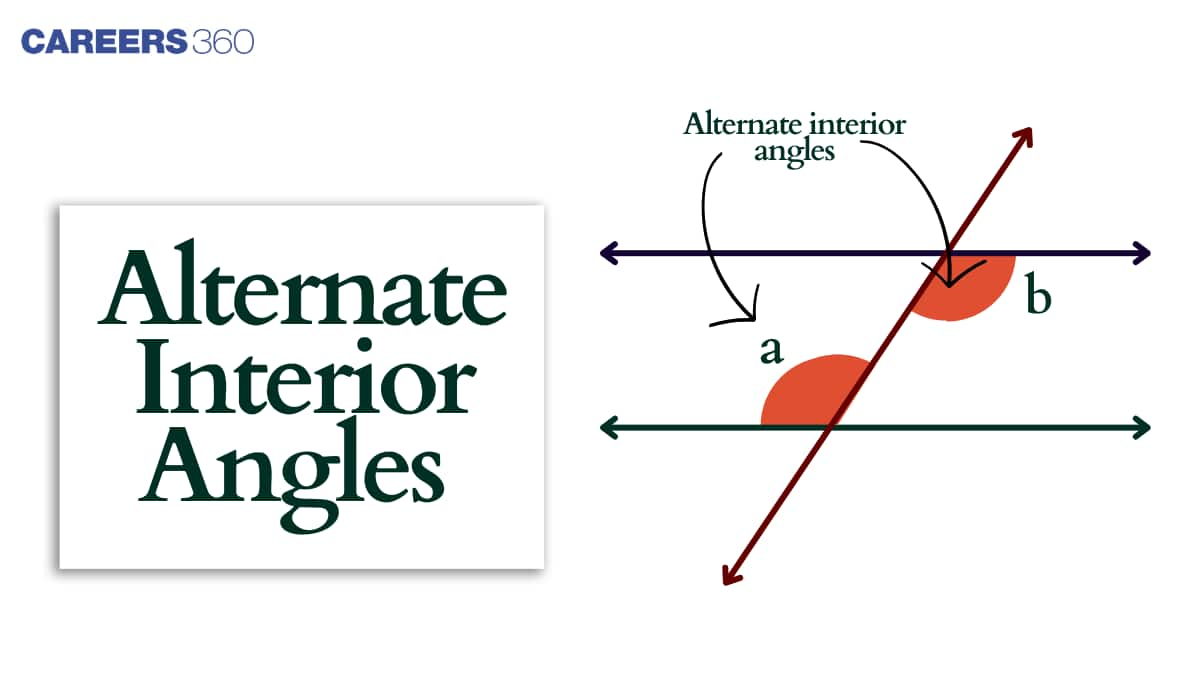
What are alternate Interior Angles?

When two parallel lines are crossed by a transversal, the pair of angles formed on the inner side of the parallel lines, and on the opposite sides of the transversal are called alternate interior angles. These angles are always equal. Sum of alternate interior angles on same side of transversal is always 180 degrees.

Alternate interior angles definition:

In the following figure, PQ, XY are 2 parallel lines cut by a transversal

Pair of alternate interior angles:

- $\angle 4$ and $\angle 6$
- $\angle 3$ and $\angle 5$

Exterior Alternate Interior Angles

They are those angles that have different vertices, lie on the alternate sides of the transversal, and are exterior to the lines. They are always equal. In the same figure, $\angle 1$ $\& \angle 7$ and $\angle 2 \& \angle 8$ are the pairs of alternate exterior angles.

What is the sum of alternate interior angles ?

The sum of alternate interior angles on the same side of a transversal is always equal to 180 degrees.

Converse of the Alternate Interior Angles Theorem

According to this theorem, if a transversal intersects two lines such that the alternate interior angles are equal, then the two lines are said to be parallel.

Proof:

In the following figure, $\angle 1=\angle 5$ (corresponding angles),
$\angle 3=\angle 5$ (vertically opposite angles).
Hence, $\angle 1=\angle 3$.
On similar grounds, we can prove that $\angle 2=\angle 4$. Hence proved.

For example: The following figure shows a map in which the road named Eleventh Avenue runs perpendicular to the $1^{\text {st }}$ Street and the $2^{\text {nd }}$ Street, which are parallel to one another. Another road named Apple Avenue makes an angle of $60^{\circ}$ with the $2^{\text {nd }}$ Street. What is the measure of angle $y$ ?

Solution: According to alternate interior angles theorem, if the two streets are parallel, and Apple Avenue is transversal, then $y$ and $60^{\circ}$ are the alternate interior angles. Hence, both the angles are equal. Hence, $y=60^{\circ}$.

Points to remember

When 2 parallel lines are cut by a transversal, following properties hold :

• Every pair of alternate interior and alternate exterior angles is always equal.
• Every pair of co-interior angles is always supplementary.
• Each pair of corresponding angles is always equal.

Co-interior Angles

They are the two angles that are on the same side of the transversal and they always sum up to 180 degrees, or are supplementary to one another.

Co-interior Angle Theorem and Proof

Statement:
If the transversal intersects the two parallel lines, each pair of co-interior angles sums up to 180 degrees (supplementary angles).

Proof:

In the above diagram, angles 3,5 are the co interior angles and angles 4, 6 are another pair of co-interior angles.

To prove: $\angle 3$ and $\angle 5$ are supplementary, $\angle 4$ and $\angle 6$ are supplementary. (replace a,b by $\mathrm{c}, \mathrm{d}$ and t by m )

Given that, c, d are parallel to each other and m is the transversal.
By the definition of linear pair,
$\angle 1$ and $\angle 3$ form the linear pair.
Similarly, $\angle 2$ and $\angle 4$ form the linear pair.
By using the supplement postulate,
$\angle 1$ and $\angle 3$ are supplementary
Hence, $\angle 1+\angle 3=180$
Also, $\angle 2+\angle 4=180$
By using the corresponding angles theorem, we can write
$\angle 1 \cong \angle 5$ and $\angle 2 \cong \angle 6$
Thus,
$\angle 3$ and $\angle 5$ are supplementary and $\angle 4$ and $\angle 6$ are supplementary.
Hence, proved.

The converse of this theorem can be stated as “if a transversal intersects two lines, such that the pair of co-interior angles are supplementary, then the two lines are parallel”.

Alternate Interior Angles Examples

Example 1: Find the measure of angle p in the following figure if the two lines are parallel and they are crossed by a transversal.

Solution: By the alternate interior angles theorem, p and $80^{\circ}$ are the alternate interior angles. Hence, they are equal. Therefore, $p=80^{\circ}$.

Example 2: In the figure below, $A B \| X Y$ and $X B \| Y Q$. If $\angle A B X=45^{\circ}$ then find $\angle X Y Q$.

Solution:
We will extend the lines in the figure to solve this.

Here, $A B \| X Y$ and $X B$ is a transversal. Thus, $45^{\circ}$ and $z$ are co-interior angles, hence, they are supplementary, i.e., $45^{\circ}+z^{\circ}=180^{\circ}, z=135^{\circ}$. Again, $X B \| T Q$ and $A Y$ is a transversal. Thus, $z$ and $\angle X Y Q$ are corresponding angles, hence, they are equal, i.e., $\angle X Y Q=z=135^{\circ}$. Therefore, $\angle X Y Q=135^{\circ}$.

Example 3: In the following figure, $\mathrm{p} \| \mathrm{q}$ and $\mathrm{r} \| \mathrm{s}$. Find the value of $\mathrm{a}+\mathrm{b}-\mathrm{c}$.

Solution:
If $p$ || $q$ and $s$ is the transversal, $b^{\circ}$ and $60^{\circ}$ are alternate interior angles. Hence, they are equal in measure (by the alternate interior angle theorem), i.e., $b^{\circ}=60^{\circ}$. Again, $s \| r$ and q is a transversal, $\mathrm{a}^{\circ}$, and $60^{\circ}$ are corresponding angles hence, they are equal, i.e., $a^{\circ}=60^{\circ}$. Now, let us assume that the angle that is adjacent to $a^{\circ}$ is $w^{\circ}$.

Since $a^{\circ}$ and $w^{\circ}$ form a linear pair, $a^{\circ}+w^{\circ}=180^{\circ}$

$
\begin{aligned}
& 60^{\circ}+w^{\circ}=180^{\circ} \\
& w^{\circ}=120^{\circ}
\end{aligned}
$

Now, $\mathrm{w}^{\circ}$ and $\mathrm{c}^{\circ}$ are corresponding angles, hence, they are equal, i.e., $\mathrm{c}^{\circ}=\mathrm{w}^{\circ}=120^{\circ}$.
Now, let us substitute the values of the angles: $a+b-c=60^{\circ}+60^{\circ}-120^{\circ}=0^{\circ}$.
Therefore, $x+y-z=0^{\circ}$

Example 4:
Find the value of e from the given below figure.

Solution:
We know that alternate interior angles are congruent.
Therefore, $5 e-30=22 e-12$

$
\begin{aligned}
& 17 e=18 \\
& e=18 / 17
\end{aligned}
$

Example 5:
Find the value of $B$ and $D$ in the given figure.(replace $B, D$ by $H, P, 45$ by 50,135 by 130)

Solution:
Since $55^{\circ}$ and P are alternate interior angles, they are congruent.
So, $\mathrm{P}=50^{\circ}$ Since they are corresponding alternate interior angles.
Since $130^{\circ}$ and H are alternate interior angles, they are congruent.
So, $H=130^{\circ}$

List of Topics Related to Alternate Interior Angles